Bonjour, je ne savais pas trop ou poser cette question...
Que représente 2 arc seconde d'angle sur une longueur de 2.5 mètres en mm, je veux me faire un niveau de haute précision et j'aurais besoin de cette info.
Merci de votre aide!
-----

Bonjour, je ne savais pas trop ou poser cette question...
Que représente 2 arc seconde d'angle sur une longueur de 2.5 mètres en mm, je veux me faire un niveau de haute précision et j'aurais besoin de cette info.
Merci de votre aide!

Bonjour, il me semble que l'arc secondé est une mesure d'écart angulaire oú un arc minute correspond a 1° du cercle et un arc seconde c'est 1/60 ème de l'arc minuté soit 1°.
A vérifier...

1 arc minute est 1/60 de degré et 1 arc seconde est 1/3600 de degré, je ne suis pas certain comment procéder les petites maths que j'ai étudié sont très loin!

Salut,
Juste pour être sur de comprendre ton problème, tu cherches la longueur représenté par un "?" dans le schéma ci dessous, c'est bien ça ?
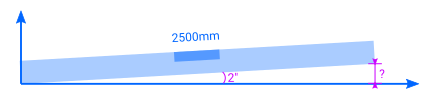
Dernière modification par Vincent PETIT ; 18/12/2019 à 00h34.
Là où il n'y a pas de solution, il n'y a pas de problème.

Le lien est en attente de validation, je te reviens, Merci!Salut,
Juste pour être sur de comprendre ton problème, tu cherches la longueur représenté par un "?" dans le schéma ci dessous, c'est bien ça ?
Pièce jointe 400948

Si c'est ça, alors tu cherches le sinus d'un angle de 2" arc, qui correspond à 2°/3600 soit quasiment rien, environ 0,000555555555556°
Il faut d'abord convertir cet angle en radian puis en faire le sinus * la longueur de ton niveau car tu cherches la longueur au bout du niveau.
sin(2°/3600*π/180)*2500mm = 0,02424mm = 24µm
Là où il n'y a pas de solution, il n'y a pas de problème.

Oui c'est exactement ça, c'est pas une grosse mesure mais c'est un peu ce à quoi je m'attendais, je te remercie beaucoup pour ton aide!Si c'est ça, alors tu cherches le sinus d'un angle de 2" arc, qui correspond à 2°/3600 soit quasiment rien, environ 0,000555555555556°
Il faut d'abord convertir cet angle en radian puis en faire le sinus * la longueur de ton niveau car tu cherches la longueur au bout du niveau.
sin(2°/3600*π/180)*2500mm = 0,02424mm = 24µm

En effet c'est peu et ce qui va rendre complexe la mesure ce sont les défauts de la surface et du niveau.
Au moindre défaut de planéité du niveau, une légère courbure, une bavure, ou autre défaut de cet ordre de grandeur (10aine de µm donc invisible) et la mesure sera incertaine, tu ne pourras pas dire si c'est le niveau qui n'est pas droit où si c'est à cause d'un défaut de surface.
Je crains qu'avec une telle précision il faille s'orienter vers une solution optique mais ça sort des Mathématiques
Bonne expérimentation
A+
Là où il n'y a pas de solution, il n'y a pas de problème.

Ce niveau servira uniquement à niveauter des tables de billard et il reposera sur des chandelles placées à différents endroits sur l'ardoise de la table. La bulle de niveau que j'utiliserai possède 10 lignes ou graduations de chaque coté représentant la mesure que tu m'as calculé pour une graduation. Les ardoises et le cadre les supportant ne sont jamais parfaits mais avec ce niveau et règle en même temps je pourrai les ajuster pour le mieux, j'ai 24 tables à niveauter et surement plus à venir.En effet c'est peu et ce qui va rendre complexe la mesure ce sont les défauts de la surface et du niveau.
Au moindre défaut de planéité du niveau, une légère courbure, une bavure, ou autre défaut de cet ordre de grandeur (10aine de µm donc invisible) et la mesure sera incertaine, tu ne pourras pas dire si c'est le niveau qui n'est pas droit où si c'est à cause d'un défaut de surface.
Je crains qu'avec une telle précision il faille s'orienter vers une solution optique mais ça sort des Mathématiques
Bonne expérimentation
A+
Merci encore pour ton aide, EL Picos!

