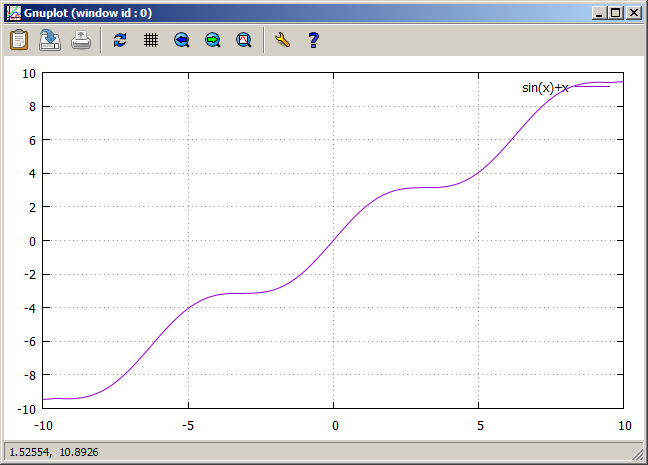
fonction inverse sin(x)+x
Discussions similaires
-
Par invitebb1c76be dans le forum Mathématiques du collège et du lycée
Réponses: 5
Dernier message: 21/04/2013, 16h57
-
Par inviteed5cf7ab dans le forum Mathématiques du supérieur
Réponses: 2
Dernier message: 03/06/2010, 19h30
-
Par invite260de47c dans le forum Mathématiques du collège et du lycée
Réponses: 3
Dernier message: 04/05/2009, 19h38
-
Par invitea871ccba dans le forum Mathématiques du collège et du lycée
Réponses: 7
Dernier message: 07/02/2008, 11h27
-
Par inviteeecca5b6 dans le forum Mathématiques du supérieur
Réponses: 4
Dernier message: 26/11/2004, 18h52