Bonjour! j'ai un problème de géométrie que je n'arrive pas a résoudre le voici:
Soit ABC un triangle qualitatif. A' est la symetrie de A à B, B' est symetrie de B à C, et C' est symetrie de C à A (ce qui veut dire A'B=BA
C'A=AC)
B'C=CB. Comptez l'aire de A'B'C' par rapport à celle de ABC.
ce que je doit trouver c'est: A(A'B'C')=1/b A(ABC)
aidez-moi s'il vous plais perssonne n'a pu m'aidé dans le forum de Mathématiques du collège et du lycée
voici le dessin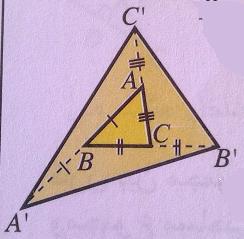
-----






 , et
, et 
 )
)