Bonjour,
Je retranscris la définition présente sur Wikipédia pour plus de clarté:
Je n'ai pas trouvé de réponse directe à ma question après recherche, je la pose donc ici:"Deux sous-espaces vectoriels F, G d'un espace vectoriel E sont dits transverses quand F + G = E. Cette condition peut être réécrite, le cas échéant, en termes de codimension :
Est-ce que cette relation codimensionnelle peut se généraliser de la même manière à plusieurs sous-espaces vectoriels de E, par exemple F, G, I ? La somme des codimensions individuelles donnant la codimension de la cointersection des trois sous-espaces vectoriels ?
-----




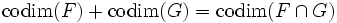

 , alors
, alors