Indice d'un lacet

[invite292e91f0]

Bonjour,
Dans le cadre d'un stage "recherche" de L3, nous avons travaillé sur un livre de topologie algébrique de Szendroi sur lequel nous avons quelques petits blocages pour deux démonstrations que nous allons utiliser dans notre rapport. Ces démonstrations traitent de l'indice d'un lacet (je ne suis pas sûr du terme... en anglais, c'est winding number). Voilà la proposition en question (désolé pour la traduction approximative...), les remarques de traduction sont en rouge et les remarques de compréhension en bleu :

On suppose que le point de base est sur l'axe des ordonnées, donc est un angle possible en coordonnées polaires. Soit un chemin avec ( désigne le disque unitaire ouvert de privé de l'origine). Alors il existe une unique application continue [TEX]r : [0,1]\rightarrow\mathbb{R_+}[\TEX] et une unique application continue [TEX]\Theta : [0,1]\rightarrow\mathbb{R}[\TEX] telles que pour tout . Si est un lacet, alors l'extrémité est ; ainsi la valeur est de la forme pour un certain entier n.

Preuve. Ecrivons et posons pour . r(t) est clairement continue et strictement positive. Puisque [0,1] est compact, r(t) admet pour bornes supérieure et inférieure R et respectivement. Définissons [TEX]\phi_{1}:[0,1]\rightarrow S^1[TEX] par ( désigne la sphère unitaire de ). Alors est continue.
Maintenant, est certainement de la forme pour un certain . Le problème est que est déterminé par l'addition de multiples de , et nous devons choisir la valeur pour chaque t afin de créer une application continue.
Clairement, l'application définie par définit un homéomorphisme de chaque intervalle ouvert [a,b] de de longueur b-a<2pi sur une section ouverte du cercle (et de même pour les intervalles fermés). Pour montrer la proposition, il suffit de couper [0,1] en de nombreux petits intervalles U_i tels que envoie chaque U_i sur une telle section, et ensuite de prendre une "branche" convenable de sur chacun d'eux. [Ici je ne suis pas sûr du terme branch. Dans le texte, "then take a suitable branch of e^-1" mais j'ignore ce que ça signifie.]
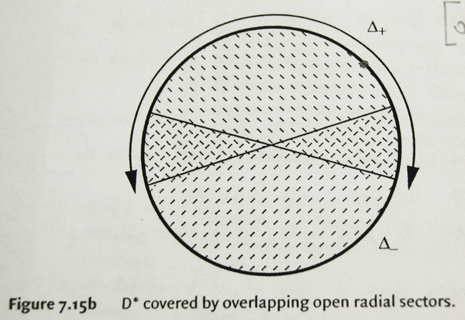
Pour faire cela de manière explicite, on couvre D* par un nombre de secteurs ouverts se chevauchant [overlapping open radial sectors] comme sur la figure suivante :

On note et les secteurs tels que et . Ecrivons (ce qui est affiché [?] est °) de manière à ce que les intervalles secteurs [sector intervals] soient et . Ensuite est divisé en les intervalles dénombrables et pour l entier relatif, de telle manière que la restriction de e à chaque intervalle [TEX]I^{l}_{\pm} soit un homéomorphisme .
[Jusque ici, nous arrivons plus ou moins à voir ce que fait l'auteur, mais nous ne comprenons pas vraiment où il veut en venir. Peut-être est-ce parce que nous ne comprenons pas la fin de la démonstration... Mais il y a beaucoup de notations introduites et nous sommes un peu perdus.]
Pour chaque t dans [0,1], l'image est dans l'un des . [Ici, grosse incompréhension. Phi_1 est censé être à valeurs dans la sphère et D* est le disque ouvert... donc je ne vois pas en quoi \phi_{1}(t)\in D*. Et ce qui nous gène le plus, c'est que ceci est beaucoup repris dans la suite de la preuve...]
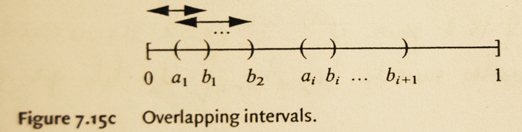
Puisque est continue, est ouvert, donc il existe un voisinage U(t) de t dans [0,1] avec . On peut supposer que chacun des U(t) est un intervalle ouvert de [0,1] (à part le premier et le dernier, qui sont des intervalles semi ouverts). Les U(t) forment un recouvrement ouvert de [0,1], donc par compacité il existe un sous-recouvrement fini. Il suit que l'on peut choisir un recouvrement de [0,1] par un nombre fini d'intervalles ouverts se chevauchant comme sur la figure suivante :

On a donc avec et [Je suppose ici que c'est a_m et non a_n, mais peut-être que je me trompe... votre avis ?], de telle manière que . (Pour chaque U_i, s'il y a le moindre doute, faire le choix de "plus" ou "moins" dès le début)
Maintenant, puisque est un homéomorphisme, on définit clairement sur comme étant [Toujours le même problème avec phi_1 : la composition d'applications définie ici est-elle vraiment possible ? On se demande si l'auteur n'a pas utilisé phi au lieu de phi_1...] et tout ce qui reste à faire est de choisir l.
D'abord, a par hypothèse, donc soit , soit . Dans le premier cas, on choisit , dans le second on prend , car on doit avoir . Ensuite, on suppose par généralisation [induction] que est définie et continue sur . Le point initial a_i de U_i est dans l'intersection avec U_i-1 de telle manière que est déjà défini ici. Cela détermine le choix de .



Voilà, merci à ceux qui ont lu jusqu'au bout, on est vraiment un peu perdus avec cette démonstration, peut-être qu'elle n'est pas si dure qu'elle en a l'air mais on a passé pas mal de temps à essayer de la comprendre (on bloque surtout sur les phi_1 qui nous semblent bizarrement utilisés...) en vain. Si jamais vous pouviez nous donner quelques conseils/indications/aides...
Merci d'avance !
-----

[invite9cf21bce]

Bonjour.

Tu as raison, je trouve, il y a beaucoup de confusions dans la démonstration entre le disque ouvert et le cercle.

Soit une application continue telle que soit le point d'affixe 1.

Pour tout t, le point est caractérisé par son argument, qui n'est malheureusement pas unique. Il s'agit de déterminer une fonction continue telle que pour tout t :



De plus, on fera en sorte que

On note et les parties ouvertes de correspondant aux angles de et respectivement.

Pour chaque valeur de , il y a un homéomorphisme ; et différent de

De même, pour tout , il y a un homéomorphisme ; et différent de

Chacun des et associe à un point, un de ses arguments.

L'idée est de "poser" si et si , avec certaines difficultés :

• il y a ambiguïté, sur le choix de n (en fait, on choisira des valeurs différentes de n pour différentes valeurs de t, bien sûr)
• si , il y a ambiguïté sur le choix de + ou de -
• on souhaite que soit continue

L'ingrédient fondamental est l'existence des .
L'histoire de compacité montre qu'il existe des réels tels que , de sorte qu'en posant , , ..., , et , alors :

quand t parcourt , reste dans ou dans

Le principe est de garder n et le signe + ou - (dans la construction de ) constants sur .

On peut d'ors et déjà choisir le signe + ou - (si jamais reste dans sur , on décide de choisir +, par exemple). Notons ce signe :

pour tout i et tout , alors

Ensuite, il faut choisir un entier pour chaque intervalle .

Pour , on peut prendre ; vu que et que les intervalles et contiennent tous les deux 0, cela revient à faire en sorte que .

Ayant choisi , ..., , on regarde ce qui se passe entre et et on s'arrange pour définir de sorte que sur

Ceci permet d'obtenir une fonction avec les bonnes propriétés.

Personnellement, je suis gêné par le découpage en deux parties (du coup, l'intersection a deux composantes et ça rend les choses moins explicites). J'aurais opté pour un découpage en trois parties, avec des intersections deux à deux qui soient connexes, c'est plus rassurant pour le recollement.

Taar.

[invite292e91f0]

Merci beaucoup d'avoir pris du temps pour nous répondre et réexpliquer cette preuve, c'est beaucoup plus clair à présent (même s'il nous a fallu un certain temps de réflexion ^^), et ça nous a même aidés à comprendre presque totalement une autre preuve qui nous posait problème.