Bonjour / bonsoir,
L'autre soir en essayant de dormir, j'ai essayé de trouver une méthode pour calculer les racines carrées à la main (chacun son truc...).
Comme j'étais déjà dans mon lit, mes idées n'étaient pas très claires et je suis parti sur une fausse piste, qui s'est révélée être... intéressante.
Voici ma "logique" :
Je cherche la racine de 10.
Je sais quefait 9, mais que
fait 16 (trop grand).
Donc je commence avec un 3.
.
Je cherche la première décimale, je multiplie donc le reste par 10 :.
De même,fait 9 et
fait 16... Je prend 3.
... et ainsi de suite, j'en arrive à 3.333333... qui est tout sauf la racine de 10
Seulement, quand on prend les chiffres un à un et qu'on les élève au carré, on obtient : 9.99999... qui vaut bien 10.
J'ai appliqué cet algorithme pour tous les entiers de 0 à 10 et j'obtiens :
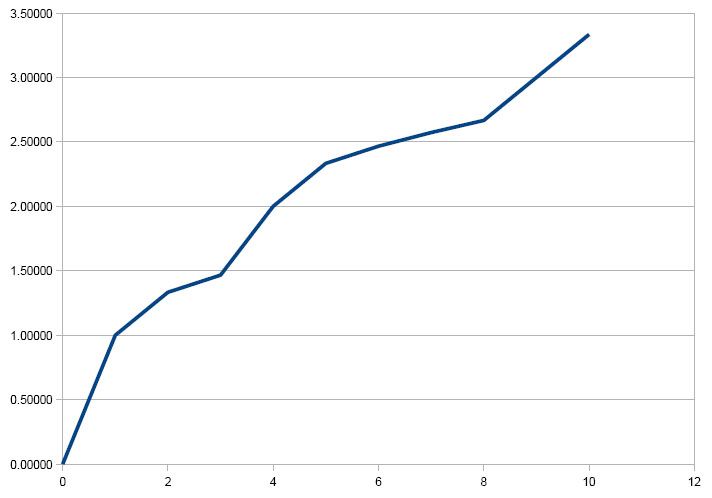
... ce qui fait une jolie courbe en "saut de puce" :Code:0 : 0 1 : 1 2 : 1.33333... 3 : 1.46666... 4 : 2 5 : 2.33333... 6 : 2.46666... 7 : 2.57333... 8 : 2.66666... 9 : 3 10 : 3.33333...
A noter que cette fonction est définie sur R. En calculant les valeurs entre 0 et 1 par pas de 0.1, on retrouve ce "saut de puce" (et par pas de 0.05, ça coince, cf. la suite)... Je suppose qu'il en va de même entre 0 et 0.1 par pas de 0.01, et ainsi de suite. C'est donc une fractale ?
Notons cette fonction, et appelons
l'ensemble des entiers dont la racine est entière.
On remarque déjà plusieurs "propriétés" :
si
.
- Si
, alors
pour tout
tel que
,
(on voit un motif qui se répète après la virgule).
- On sent bien que F est discontinue pour tout
.
- On peut penser qu'elle est continue sur tout ce qui reste de R.
Le lendemain j'ai écrit un programme pour calculer plus de valeurs (à la main c'est fatiguant... même si c'était le but), et j'ai été surpris de voir des erreurs apparaitre à partir de
!
Testez vous-même :
et
, on prend 3, reste
.
et
, on prend 7, reste
.
... et on ne peut pas aller plus loin. Admettons : on prend 9, reste
...
Problème : le reste "augmente" petit à petit, et on ne peut rien faire pour l'en empêcher.
... sauf si on se permet de prendre des "chiffres" plus grands que 9 !
Allons y, pour voir...
Le début ne change pas :
et
, on prend 3, reste
.
et
, on prend 7, reste
.
,
,
, on prend 10, reste
.
, on a terminé : F(15) = "3. 7 10 10", autrement dit "3.7aa".
Grâce à cette astuce, j'ai réussi à calculer.
... et je tombe à cours de symbole pour 3967.
Je suppose que tout ça manque un peu de rigueur... je mélange les bases allègrement.
J'aurai peut être dû m'arrêter à 15...
Quoi qu'il en soit, est-ce que cette "fonction" vous dit quelque chose ?
Que représente cette suite :
... et qu'a-t'on après u5 ?Code:u0 = 0.0000 = 000/300 ( = sqrt(0)/3 ) u1 = 0.3333 = 1/3 = 100/300 ( = sqrt(1)/3 ) u2 = 0.4666 = 2/5 + 2/30 = 14/30 = 140/300 u3 = 0.5733 = 1/2 + 7/100 + 1/300 = 172/300 u4 = 0.6666 = 2/3 = 200/300 ( = sqrt(4)/3 ) u5 = 0.7333 = 7/10 + 1/30 = 220/300
PS : Une fois avoir mis en place l'astuce des "bases", j'ai donc calculé F(x) jusqu'à x = 3966, puis converti les résultats en base 10, en supposant que ceux-ci étaient écrits en base 36 (les 10 chiffres plus les 26 lettres de l'alphabet) : les curieux pourront voir >> ici << le résultat dessiné sous Open Office.
-----






 .
.