Distributions de k éléments dans n avec contraintes

[invite518c8190]

Bonjour,

Pour résumer:

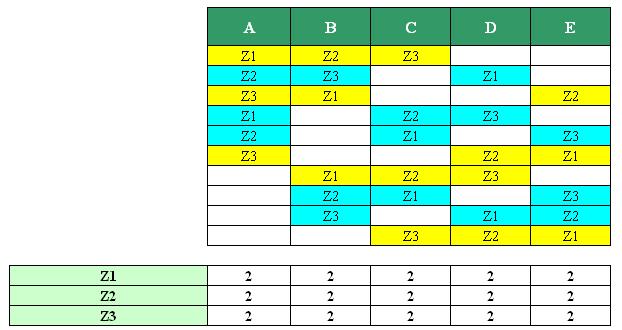
je cherche à distribuer k éléments parmi p possibles, chaque élément distribué est noté (Z1, Z2 ... jusqu'à Z(k) ).
Je sais déterminer toutes mes combinaisons pour distribuer mes éléments dans ma matrice, mais le problème c'est que j'ai une contrainte supplémentaire : les éléments distribués doivent être "à l'équilibre", cad autant de Z1,Z2... par colonne pour chaque colonne.
Pour illustrer simplement ce dont je parle voir le fichier Excel :

http://dl.free.fr/e3krgqyzA

J'avais prévu de distribuer mes Zi de la manière suivante (exemple 3 éléments)
Z1 Z2 Z3
Z2 Z3 Z1
Z3 Z1 Z2
Z1 Z2 Z3
etc.. en avançant dans le vecteur. Bien évidemment ce n'est pas équilibré

Avez-vous une idée sur la séquence des Zi que je dois utiliser? Et surtout est-ce possible ?

Merci d'avance
Cladoo
-----

[invité576543]

Y-a-t'il une contrainte sur le nombre de lignes ?

[invite518c8190]

Non, le nombre de ligne est simplement multipe de C(k,n), donc dans mon exemple : au minimum C(3,5) =10 lignes.
Une fois que je connais la séquence de distribution des Zi pour 1 bloc, je peux la répéter pour chaque 'bloc'.

[invité576543]

Pourquoi un multiple de C(k, n) ?

Le nombre de possibilités distinctes, c'est A(k,n), soit 5x4x3 = 60 dans le cas tabulé.

Si on veut faire un bloc à répéter, ce serait plutôt de A(k,n) lignes, il me semble.

[A voir en vidéo sur Futura]

[invite518c8190]

ça voudrait dire que je ne peux pas être équilibré au sein d'un bloc de C(k,n)?

Pourtant j'arrive à trouver l'équilibre sur un bloc de 10 lignes C(3,5):


est-ce dû au hasard et non généralisable ?

[invité576543]

ça voudrait dire que je ne peux pas être équilibré au sein d'un bloc de C(k,n)?

Non, bien sûr.

Je cherchais juste à comprendre pourquoi C(k,n), en particulier si c'est une contrainte dans le problème, plutôt qu'un choix dans les solutions.

est-ce dû au hasard et non généralisable ?

La question est alors si on peut toujours trouver C(k,n) cas parmi les A(k,n) possibilités tel que les colonnes soit équiréparties.

Un cas extrême est k=n, on alors C(k,n)=1, et il est manifestement impossible, pour n>1, de trouver une ligne telle que les colonnes soient équiréparties, non?

[invite518c8190]

En fait le but est de créer des randomisations équilibrées (en terme d'affectation et en terme de Zi) avec le moins de lignes possibles. Chaque ligne représente un sujet (une souris) et chaque Zi représente une zone sur celle-ci.

Le problème c'est que par exemple dans un cas C(3,6)=20, je ne peux pas m'en sortir (être équilibré) avec 20 lignes (cf. 20/3).
Reste la possibilité de faire des blocs avec toutes les possibilités en utilisant les arrangements, donc forcément équilibrés en terme de Zi. Exemple A(3,5)=60 mais comme évoqué précédemment ça m'ennuie d'avoir à utiliser 60 observations pour atteindre l'équilibre alors qu'avec 10 lignes c'est possible (cf. image ci-avant). La raison est purement économique.

Du coup comme il n'est pas possible de 'générer' des blocs d'observations multiple de C(k,p) toujours équilibrés en terme de distributions de Zi pour n'importe quel k et p (cf C(3,6)), est-ce forcément nécessaire de créer des blocs multiples de A(k,p) pour généraliser l'algorithme, kit à faire passer à la trappe les cas un bloc multiple de C(k,p) serait possible?

[invité576543]

est-ce forcément nécessaire de créer des blocs multiples de A(k,p) pour généraliser l'algorithme

Non, pas forcément...

La question devient alors quelle est le nombre minimum de combinaisons parmi les A(k,p) donnant des colonnes équilibrées, et comment construire une solution pour ce minimum.

On arrive vite à voir qu'il faut au moins p combinaisons (p lignes).

Et il y a toujours une solution avec p lignes, suffit de faire les p permutations circulaires d'une ligne quelconque.

On peut en déduire que tout multiple de p est possible, et se construit en prenant n combinaisons et leurs permutations circulaires.

Mais ce ne sont pas les seules solutions, celle dans le fichier excel n'entre pas dans cette catégorie.

[invite518c8190]

Et il y a toujours une solution avec p lignes, suffit de faire les p permutations circulaires d'une ligne quelconque.

On peut en déduire que tout multiple de p est possible, et se construit en prenant n combinaisons et leurs permutations circulaires.

Mais ce ne sont pas les seules solutions, celle dans le fichier excel n'entre pas dans cette catégorie.

Excuse moi mais je ne suis vraiment pas à l'aise avec la théorie, aurais-tu quelques exemples?
Le truc c'est que je ne comprends pas comment ça peut être équilibré si on considère seulement p lignes, en effet dans le cas C(3,5) j'ai 10 lignes, elles sont nécessaires pour faire apparaître toutes les combinaisons possibles de 3 parmi 5, alors comment seulement la moitié (k=5) peuvent-elle donner l'équilibre recherché?

En fait,ce que je n'ai peut-être pas précisé, c'est que le nombre de Zi doit être équilibré par colonne (autant de Z1, que de Z2 etc..) mais je dois également obtenir un équilibre inter-colonne (autant de Z1 pour A que pour B que pour C etc...)

[invité576543]

en effet dans le cas C(3,5) j'ai 10 lignes, elles sont nécessaires pour faire apparaître toutes les combinaisons possibles

Elles ne font pas apparaître toutes les combinaisons possibles, puisqu'il y a 60 combinaisons différentes !

Dans le fichier, la combinaison Z2 Z1 Z3 - - n'apparaît pas, par exemple.

Excuse moi mais je ne suis vraiment pas à l'aise avec la théorie, aurais-tu quelques exemples?

Z1 Z2 Z3 - -
- Z1 Z2 Z3 -
- - Z1 Z2 Z3
Z3 - - Z1 Z2
Z2 Z3 - - Z1

(avec "-" pour indiquer un vide.)

Maintenant, ce qui n'apparaît pas dans une telle liste, c'est toutes les combinaisons de cases vides. Mais une telle contrainte n'a pas été précisée !

[invite518c8190]

D'accord je comprends.

En fait je dois faire apparaitre toutes les combinaisons possibles : C(k,p)
par contre je n'ai aucune contraintes sur les séquences de Zi (ou leur permutations) du moment que j'atteins l'équilibre final (je peux répéter la même séquence x fois ou ne pas en faire apparaitre certaines).

Pense-tu cela jouable avec ces contraintes?

Pour les combinaisons de cases vides, je n'ai pas de contraintes.

[invité576543]

En fait je dois faire apparaitre toutes les combinaisons possibles : C(k,p)

Je n'ai toujours pas compris de quelles C(k,p) combinaisons il s'agit!

Dans mon exemple de 5 lignes, à quoi ressemblent les 5 manquantes ? (L'exemple respecte bien les contraintes des colonnes : il y a exactement 1 Z1, 1 Z2 et 1 Z3 dans chaque colonne, non?)

[invite518c8190]

Je n'ai toujours pas compris de quelles C(k,p) combinaisons il s'agit!

Dans mon exemple de 5 lignes, à quoi ressemblent les 5 manquantes ? (L'exemple respecte bien les contraintes des colonnes : il y a exactement 1 Z1, 1 Z2 et 1 Z3 dans chaque colonne, non?)

En jaune : les combi présentées
En bleu : les combi manquantes

[invité576543]

Cela ressemble pas mal à ce que j'ai appelé "toutes les combinaisons [de position] de cases vides", alors. C'est bien une contrainte sur les cases vides, à mon sens.

OK

Si on prend C(k,p) lignes correspondant à toutes les combinaisons de cases vides possibles, chaque colonne contient (p-k)C(k,p)/p cases vides, soit C(k, p-1) (soit C(3,4) dans le cas exemple, soit 4, comme on peut le vérifier).

Pour que ce soit équilibré, il faut comme condition nécessaire que C(k,p)-C(k, p-1)= C(k-1,p-1) soit un multiple de k, ce qui n'est pas le cas général. Par exemple C(2-1, 4-1)= 3 n'est pas un multiple de 2. Avec 2 valeurs, 4 colonnes et C(2,4)=6 lignes on ne peut pas équilibrer (on a trois cases non vide par colonne).

D'où une condition nécessaire : C(k-1,p-1) multiple de k.

On peut se poser la question si elle est suffisante... Je ne sais pas répondre rapidement...

[invite518c8190]

Cela ressemble pas mal à ce que j'ai appelé "toutes les combinaisons [de position] de cases vides", alors. C'est bien une contrainte sur les cases vides, à mon sens.

Autant pour moi je n'avais pas compris ta question sur les cases vides

On peut se poser la question si elle est suffisante... Je ne sais pas répondre rapidement...

Ne t'en fais pas, tu m'a déjà beaucoup aidé, et permis d'avancer dans mon problème, c'est plus qu'appréciable, d'autant que rien ne t'y oblige. J'apprécie l'aide fournie et le temps passé, crois moi. Si tu as une idée qui te vient je suis preneur mais ne te prends pas trop la tête

De toute façon je pense que je vais laisser une option d'équilibrer à de manière "brute" en distribuant chaque permutation de k éléments dans chaque combinaisons de k parmi n. Je serai forcément à l'équilibre, mais par contre l'explosion du nombre de lignes (souris) augmente énormément et ça ne me plait pas trop... Si seulement je savais que c'est le seul moyen, je renoncerait à tout autre moyen, mais quand je vois qu'il est possible d'équilibrer un C(3,5) sur 10 lignes au lieu des 60 lignes prévues par le A(3,5) ça me laisse un goût amer...

Bref si tu entrevois une solution et bien

Merci de ton aide précieuse!!