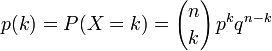Problème en proba

[evanicon]

Bonjour je suis en 2e année de bio et en ce moment nous faisons des exos de probabilités le truc c'est que j'essaye avec tous les types d'exercices comme ça quoi qu'il arrive à l'examen je ne serai pas troublée par l'énoncé et je pourrai le résoudre. Mais là je sèche un peu:

Exercice 16 : Les valeurs prises par une variable aléatoire X, suivant une
loi binomiale de paramètres n et p, sont affichées par un compteur de la façon
suivante :
– Si X prend une valeur non nulle, le compteur affiche correctement cette
valeur ;
– Si X prend la valeur 0, alors le compteur affiche n’importe quoi, au
hasard entre 1 et n.
On note Y la variable aléatoire coorrespondant au nombre affichée par le compteur détraqué.
1. Déterminez la loi de Y .
2. Calculez son espérance

L'énoncé vient de là http://ddlecs1.free.fr/Documents/td23.pdf

Mes réponses:

1. Y(oméga)={0,1,...,n}
P(Y=k)= C(k parmi n)*p^k*(1-p)^n-k

2.E(Y)=n*p

Merci de votre aide

Evanicon
-----

[evanicon]

Bah alors pas de réponses je ne demande pas qu'on me corrige l'exercices mais qu'on me donne un petit coup de pouce

[inviteea2fb8cf]

Ben... Ce que tu as répondu, c'est correct pour une loi binômiale avec les bons paramètres, en l'occurrence pour . Pas pour , dont la loi n'est pas binômiale.

Indice : si Y prend la valeur , c'est ou bien parce vaut , ou bien parce que vaut et que le compteur affiche, par hasard, . Et ces deux évènements sont disjoints.

[evanicon]

Ah oui c'est vrai P(X=k)= C(k parmi n)*p^k*(1-p)^n-k
X(oméga)={0,...,n} X prend soit la valeur O soit valeur non nulle mais les valeurs prises dans R donc on peut avoir une infinité de nombre donc on peut aller jusqu'à n

Si les 2 évènement sont disjoints est ce qu'on dire qu'ils sont indépendants??

Dans ce cas P(X=k)*P(Y=k)=P(X=k)interP(Y=k )

[A voir en vidéo sur Futura]

[NicoEnac]

Bonjour,

– Si X prend la valeur 0, alors le compteur affiche n’importe quoi, au
hasard entre 1 et n.

Est-ce là l'énoncé exact ? "Le compteur affiche n'importe quoi, au hasard entre 1 et n" ? Au hasard certes mais suivant quelle loi ? Uniforme ? Je suppose que c'est le cas mais l'énoncé n'est pas très bien posé.

Sinon Garf te dit que la probabilité que Y affiche k, c'est qu'au premier tirage il tire k ou qu'il tire 0 et affiche k parmi [1;n]. Ces événements étant disjoints, leurs probabilités s'ajoutent.

[evanicon]

Le compteur affiche de façon aléatoire et équiprobable des valeurs entre 1 et n

Si les 2 événements s'ajoutent donc :
P(X=k) + P(Y=k)= [P(X=k)unionP(Y=k)] - [P(X=k)interP(Y=k)]
De mm pour P(X=0)

Je ne vois pas vraiment en quoi ça répond à la question qui était "donner la loi de Y" :

[inviteea2fb8cf]

Non, voyons ! Il faut faire attention à ce que l'on calcule, et ne pas mettre des et des partout !

Soit non nul :



Maintenant, comme les évènements et sont disjoints, on a :



Que vaut ? Que vaut ?

~~~~~

Un petit rappel.

On dit que deux évènements sont disjoints s'ils ne peuvent pas arriver en même temps, i.e. si leur intersection est vide. Par exemple, et sont disjoints. Si et sont deux évènements disjoints, alors . Dans le petit exemple que je viens de prendre, cela se traduit par le fait que la probabilité d'obtenir "0" ou "1" est la probabilité d'obtenir "0" plus celle d'obtenir "1".

On dit que deux évènements sont indépendants si la survenue de l'un n'influence pas celle de l'autre (et vice-versa). Par exemple, si X désigne le résultat d'un lancer de dés et X' le résultat d'un autre lancer de dés tout à fait... eh bien, indépendant, alors et sont disjoints. Si et sont deux évènements disjoints, alors . Dans le petit exemple que je viens de prendre, cela se traduit par le fait que la probabilité d'obtenir deux "1" en lançant deux dés est de 1/6*1/6 = 1/36.

[evanicon]

Événements disjoints ça veut donc dire incompatible

Je récapitule:

Quand X(omega)=[1,...,k} donc Y(omega)={0,...k}
Quand X(omega)= {0} donc Y(omega)= {1,...,n}

P(X=k)= C(k parmi n)*p^k*(1-p)^n-k

P(X=0 et Y=k)= (1/n) car quand X=0 la loi de Y prend des valeurs de façon aléatoire et équiprobables alors:
P(X=0 et Y=1) = ... =P(X=0 et Y=n) = (1/n)

Donc l’espérance de Y ne dépend que de celle de X qui suit une loi binomiale :
E(X)= np

[evanicon]

Personne pour me dire si c bon ou pas???

C'est un exercice d’entrainement j'ai fait les exos de proba sur les anniversaires, les tirages de boules avec et sans remise, tirage de cartes mais là je sèche ça veut dire que il faut que je sache le faire sinon si je tombe sur ça à mon exam final...

[inviteea2fb8cf]

Le problème, c'est que si je continues, je vais finir par faire l'exercice à ta place. Parce que oui, c'est encore faux.

Quand X(omega)=[1,...,k} donc Y(omega)={0,...k}
Quand X(omega)= {0} donc Y(omega)= {1,...,n}

Premièrement, c'est du charabia. "Quand ... donc" ne veut strictement rien dire ; ce n'est pas une question de mathématiques, mais de syntaxe. Utilise plutôt "Si ... alors", " ... donc ..." ou d'autres structures du même genre qui on l'avantage d'être compréhensibles (y compris par celui qui corrige si tu passes un examen). Pas la peine d'être imaginatif dans les formulation, le tout est d'être correct.
Deuxièmement, je ne sais pas ce que veulent dire ces , ces égalités ensemblistes ou autres, mais je conseillerais de l'oublier. Le principal est d'écrire des choses que l'on comprend, et j'ai l'impression que ce n'est clairement pas le cas ici.
Une remarque au passage : si tu as des problèmes pour écrire des symboles mathématiques, n'essaye pas de faire quelque chose qui ressemble avec les caractères disponibles sur le clavier. Ecris en français.

P(X=k)= C(k parmi n)*p^k*(1-p)^n-k

P(X=0 et Y=k)= (1/n)

Tu es en train de me dire que . Tu te rends comptes qu'alors est plus grand que ?


Bref. J'en reviens à ton sujet. Je vais changer légèrement l'énoncé (ce qui ne changera absolument rien aux réponses aux questions !).

Soit X une variable aléatoire suivant une loi binomiale de paramètres n et p. Soit Z une variable aléatoire de loi uniforme sur {1, ..., n} indépendante de X.

On définit une variable aléatoire Y de la façon suivante :
* Si X>0, alors Y=X ;
* Si X=0, alors Y=Z.

1) Quelle est la loi de Y ?
2) Calculer l'espérance de Y.

Je te laisse vérifier que c'est exactement la même chose que ton énoncé, simplement formulé de façon un peu différente.

Maintenant, on sait que, pour tout entier strictement positif :

C'est ce que j'ai dit dans mon précédent message.
Tu sais déjà ce que vaut . Maintenant, tout ce que je te demande de calculer, c'est . Indice : X et Z sont indépendantes, et regarder mon message précédent.

Enfin, pour calculer l'espérance : n'essaie pas de faire des raisonnements du type "l’espérance de Y ne dépend que de celle de X", qui vont être faux. Une fois que tu connais la loi de Y, pose explicitement la formule qui te donne son espérance, et calcule.

[evanicon]

Avec quel logiciel tapes tu les formules mathématiques?
Parce que quand je tape X(omega) je voulais taper la lettre grecque

A la relecture et après un peu de recul je m’aperçoit que P(X=0 et Y=k)= (1/n) c'est faux en fait c'est plutôt P(Y=k|X=k)= P(X=0 et Y=k)/ P(Y=k)

comme les 2 événements sont disjoints:
P(X=0 et Y=k)= P(X=0)*P(Y=k)

[evanicon]

Ce que je voulais taper pour la loi de X c'était ça

[evanicon]

si P(X=0 et Y=k)= P(X=0)*P(Y=k)

alors au final on se retrouve avec
P(Y=k)= P(X=k) + P(X=0 et Y=k)
P(Y=k)= P(X=k) + [P(X=0)*P(Y=k)]

et donc P(Y=k)= P(X=k)/[1-P(X=0)]

[evanicon]

Est ce que c'est ça où je m'égare??
Garf: le but n'est évidemment pas de faire l'exo à ma place j'essaye de comprendre cet exercice qui ne doit as être plus compliqué que les autres qd mm!!!