Polynôme d'interpolation (de Lagrange ?) avec une inconnue supplémentaire

[Philou67]

Bonjour,

Je me propose d'approximer une fonction dont je connais la forme par quelques points caractéristiques. Il s'agit d'une puissance (en W) en fonction du temps (en h) :



Je me propose d'approximer cette fonction à l'aide d'un polynôme d'interpolation de degré 4


Bien entendu, je ne connais pas P_max et c'est bien là tout l'objet de mon étude.
En revanche, je sais que la surface de cette courbe pour vaut E, dont je connais la valeur (en Wh).
Je me propose alors d'ajouter cette équation :

soit

(E = 96kWh).

Je dispose alors du système d'équations suivant :


Je me propose alors de résoudre le système d'équation à l'aide de la représentation matricielle suivante :


En résolvant numériquement, par le pivot de gauss par exemple (en fait, j'ai utilisé la fonction Excel/Calc LINEST ou DROITEREG), ce système d'équation, j'obtiens des résultats qui me permettent de vérifier avec les points que je connais, que les coefficients a, b, c, d, e, f et P_max sont corrects (les équations sont vérifiées avec une erreur faible.
Cependant, P_max ne correspond pas à la valeur attendue, et lorsque je calcule p(T₀), il ne vaut pas P_max. Du coup, il y a une erreur soit dans mes calculs, soit dans mon raisonnement.

Au besoin, si c'est nécessaire, je peux ajouter une condition supplémentaire : p'(T₁₀₀) = 0.

Pourriez-vous m'aider à trouver mes erreurs ?
Pourriez-vous m'aider à trouver une solution à mon problème ?

Je vous serais reconnaissant d'être indulgent avec moi, les mathématiques étant un trop lointain mais néanmoins agréable souvenir
-----

[NicoEnac]

Bonjour,

Qu'obtiens-tu comme valeurs pour a, b, c, d, e et Pmax ? Je l'ai fait sous excel mais j'obtiens des valeurs pas très catholiques.

[NicoEnac]

Re,

J'ai corrigé mon erreur (très bête comme d'hab).

Ton raisonnement est correct.

Je trouve :
a = -5,9872E-06
b = 0,000750729
c = -0,027698689
d = 0,313947861
e = 0
Pmax = 1,040932383

Tu peux vérifier mais avec ces valeurs, on a bien que p(6) = Pmax, p(17) = Pmax/2, p(35) = Pmax/4 et p(70) = 0

Edit : de plus, j'ai tracé la courbe et ça donne un truc qui n'est pas cohérent du comportement de ton système je pense. En effet, p(t) devient négatif entre 24 et 32 puis culmine en t = 58 à une valeur qui vaut 3.5.Pmax...

Puis-je te demander quel système est modélisé par ces points ? Car je pense qu'une simple exponentielle décroissante sera suffisante à partir de t =6.

[Philou67]

Je trouve :
a = 9.45E-8
b = 1.18E-5
c = -4.37E-4
d = 4.96E-3
e = 1.37
Pmax = 1.64E-2

Mais j'ai soudain un gros doute, car je me retrouve avec un coefficient supplémentaire qui ne m'est pas utile pour p(t) (le a₀ correspondant à cette explication).

[A voir en vidéo sur Futura]

[NicoEnac]

Rere,

Je me permets d'ajouter qu'ajouter comme contrainte que p'(T₁₀₀) = 0 est une très bonne idée. Il faut cependant augmenter le degré de ton polynôme d'interpolation. En effet, pour l'instant tu viens de trouver l'unique polynôme de degré 4 passant par tes points. De degré 5, il en existe une infinité. En fixant p'(T₁₀₀) = 0 tu limites le nombre de polynômes solutions à 1.

[NicoEnac]

Je trouve :
a = 9.45E-8
b = 1.18E-5
c = -4.37E-4
d = 4.96E-3
e = 1.37
Pmax = 1.64E-2

Je peux déjà te dire que ta solution n'est pas bonne. En effet, p(0) = e = 0 d'après tes données. Or là tu trouves e = 1.37.

[Philou67]

Croisement : déjà, on n'a pas les mêmes valeurs, et ce qui me réconforte, c'est que tu ais des données correcte, même si le degré du polynôme est peut-être mal choisi.

Voici la forme de la courbe :
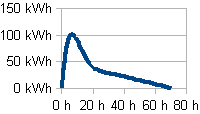(unité incorrecte pour l'axe des Y).

[Philou67]

Oui, au début, j'avais pris e=0 comme hypothèse de départ, et j'avais fait le calcul, mais sans trouver de réponse correcte non plus.

[NicoEnac]

Bon je suis désolé pour toi mais j'ai fait le calcul en rajoutant comme hypothèse que p'(T₁₀₀) = 0. J'ai trouvé le polynôme de degré 5 qui répond à tes hypothèses ainsi qu'à cette supplémentaire. Et le polynôme n'a toujours pas la tronche que tu recherches.

a = -2,12E-07
b = 2,98E-05
c = -1,39E-03
d = 2,67E-02
e = -1,94E-01
f = 0
Pmax = -4,70E-01

Tu peux le tracer et ce n'est pas du tout ça...

[Philou67]

Ceci révèle-t-il un phénomène de Runge ?

Je vais devoir comprendre pourquoi mes résultats sont différents des tiens pour commencer, et peut-être étudier une autre méthode d'interpolation. Si vous avez une idée, je suis preneur.

En tout cas, merci NicoEnac

[NicoEnac]

Ceci révèle-t-il un phénomène de Runge ?

Sans doute car quand on les trace on voit qu'ils oscillent dans [0;70] alors que ce n'est pas le comportement qu'on attend d'eux (plutôt celui de coller le plus possible au tracé que tu as joint plus haut).

Je vais devoir comprendre pourquoi mes résultats sont différents des tiens pour commencer

Modestement, je pense que mes solutions pour le polynôme de 4ème degré et de 5ème degré sont bonnes (je les ai tracées et ils vérifient toutes les hypothèses).

En tout cas, merci NicoEnac

C'est normal entre Alsaciens

[Yoghourt]

Comme piste alternative, je suggère une loi de Weibull.

Elle a le bon goût d'avoir une tête qui ressemble à ce que l'intuition dicte. De plus, passé le pic, elle tend à se comporte en exp(-a.x), ce qui correspond au type de loi suivie par une relaxation thermique par conduction/convection.

[Yoghourt]

Addendum : les solutions avec source de chaleur montrent des lois à base de erf(f(t)) et exp(-at), pas cool...

[Yoghourt]

addendum 2 : pour la relaxation thermique par rayonnement, c'est la loi de stefan-boltzman qui s'applique plutôt que la loi de fourier : P = sigma.T^4

Autrement dit, on sait que ce n'est pas une loi en T^5
Euh, désolé pour le "cadeau"...

[NicoEnac]

elle tend à se comporte en exp(-a.x),

C'est aussi l'impression qu'elle me donnait mais je me trompais. Car à t = 6, on est à P_max. A t = 17 (soit 9h plus tard), on est à P_max/2. Or une des propriétés de l'exponentielle décroissante est que le temps qu'il lui faut pour "se diviser" par un nombre reste contant. Autrement dit, s'il faut 9h pour que la puissance passe de P_max à P_max/2, alors il lui faudra 9h pour passer de P_max/2 à P_max/4.

Cela est contredit par les données : On passe de P_max à P_max/2 en 9h (17-6), de P_max/2 à P_max/4 en 18h (35-17).

[Philou67]

Il y a en fait deux phénomènes physiques qui entrent en jeu dans cette courbe de puissance :
- un phénomène qui accumule de l'énergie produite
- un phénomène qui libère l'énergie accumulée
Les deux phénomènes sont indépendant :
- le feu dans un poêle entre T₀ et T₀+2 (environ), qui transmet la chaleur à une masse
- la masse qui émet entre T₀ et T

Au milieu, il y a des transferts thermiques par conduction, convection et rayonnement.

[NicoEnac]

Le feu ne transmet la chaleur que sur 2h ? Alors comment se fait-il que la courbe soit croissante jusqu'à t = 6h ?

[Philou67]

A cause de l'inertie... la masse continue de se charger à l'intérieur, et la température "extérieure" continue donc de monter (ainsi que la puissance du coup)

[Philou67]

Pour interpoler des courbes de température à partir de relevés (non périodiques), j'ai utilisé la méthode du spline cubique de Hermite (note : cette page wiki n'est référencée dans aucune page relative aux interpolations, c'est bien dommage). Le résultat était parfait. Il nécessite de connaitre les dérivées en chaque point. Je peux prendre par approximation, des valeurs arbitraires (par exemple en T₁₀₀, 0) ou calculée par rapport à la pente linéaire entre deux points (par exemple en T₅₀ -1/2). En revanche, je n'ai pas de moyen simple, à première vue, de calculer Pmax. Ceci pourrait-il être une piste malgré tout ?

Merci également à Yoghourt pour sa participation.

[NicoEnac]

OK donc si j'ai bien compris, le feu est allumé pendant 2h puis s'éteint mais il continue de chauffer la masse jusqu'à t = 6h car sa température reste supérieure à celle de la masse. Puis la masse dégage de la chaleur et se refroidit peu à peu.

[Philou67]

C'est cela, sauf que le foyer baisse assez vite en température (de plus de 600°C à moins de 300°C), mais la chaleur doit traverser d'épaisses couches de matériau à forte capacité thermique dont la température est nettement inférieure (30/35°C pour la plus extérieure).
En fin de feu, le foyer est plus ou moins "isolé", de sorte qu'il ne peut évacuer sa chaleur que par la masse (c'est une approximation, mais les pertes sont déjà comptées par ailleurs, donc c'est tout à fait réaliste).

[Yoghourt]

Pour revenir à ma suggestion à 2 centimes et l'assumer un peu, voici mes petites notes. Désolé, c'est pas aussi bô que le message initial de Philou67 en Tex... (texisé )
----------------------------------------





k est appelé le paramètre de forme, et lambda est appelé paramètre d'échelle.

atteint son maximum en x tel que :


La position de ce maximum est notée ________________ [1]
Ouf, on retrouve bien la formule du mode de Weibull indiquée dans wikipédia. On note que lambda joue bien son rôle d'échelle pour les x.

La maximum vaudra alors :
_____________________ [2]

Il est très intéressant de noter que le maximum de ne dépend pas de dès lors qu'on connait .

______________________________ ______________________________ ____________________
On cherche à approximer une fonction P avec une densité de Weibull. On pose :

.
Il vient de suite puisque :


On note le maximum de P, c'est à dire
_________________ [3]

Sans grosse surprise, exprimé avec ne dépend pas du facteur d'échelle , ce qui est bien pratique. Enfin je crois.

Les inconnues sont . Pour l'instant, on a 2 équations (non linéaires).
En sus, on connait et



ou encore en n'utilisant aucune des équations précédentes :

Pas sûr que ce soit beaucoup mieux...

Peut-être faut-il creuser un peu plus, ou laisser tomber la partir analytique à ce stade et passer au crible (fonction cible sous tableur)

Il est intéressant, quand même, de noter qu'on peut rechercher et k indépendamment de la connaissance de . Et raccrocher dans un 2e temps via E et la formule [3]

[Yoghourt]

Woah, bravo Philou et merci pour la latecisation

Addendum - suggestion de stratégie pour le crible :
- faire varier k
- en déduire Pmax de E&k et lambda de T100&k
- chercher à minimiser l'erreur quadratique sur T50 et T25

[Yoghourt]

(en espérant qu'au bout du compte, ça se termine pas comme l'épilogue de la dinde au whisky où le résultat est tout à foutre à la poubelle et nettoyer l'bordel, dans l'absence de joie et la mauvaise humeur ... )