Bonjour à tous,
Avant tout il s'agit d'un problème mécanique, donc sa résolution semble être du domaine de la géométrie.
Je vais essayer de l'expliquer du mieux que je peux.
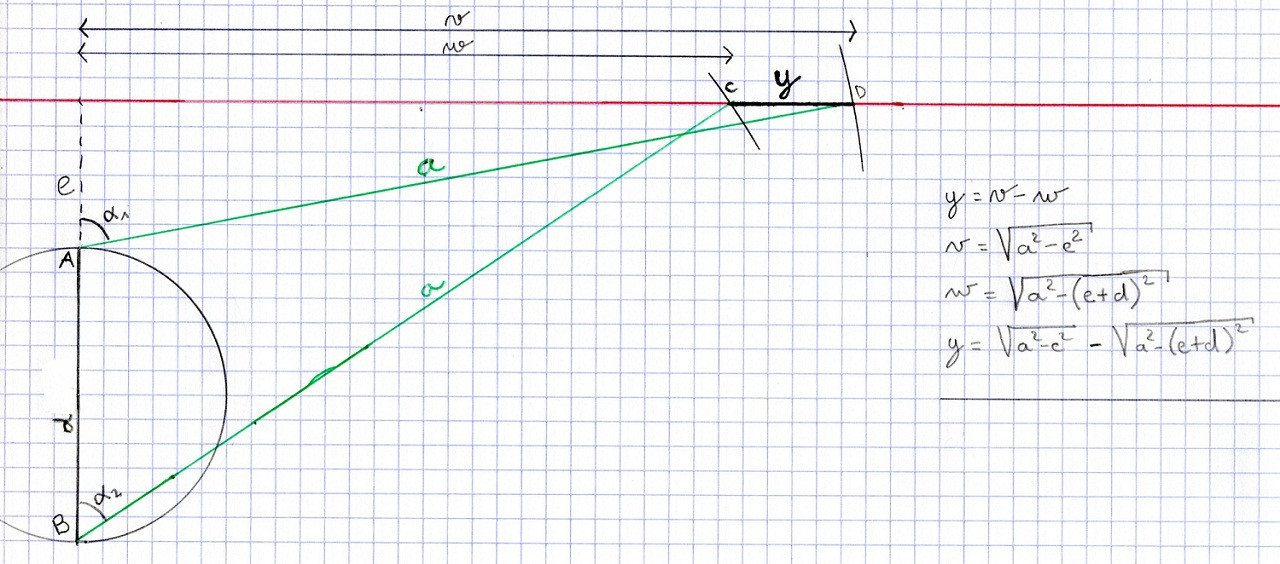
Donc il y a un cercle de diamètre "d" qui représente une roue à laquelle est attaché en "A", une bielle de longueur "a". L'autre extrémité de cette bielle "a" coulisse en un point "D", le long de la droite rouge.
Quand le cercle a fait un demi-tour complet, la bielle de longueur "a" sera alors entre les points "B" et "C".
Avec ceci la droite rouge est exactement perpendiculaire au diamètre d.
Dans un premier temps, si l'on connait "d", "e" et "a", alors il est possible de calculer la longueur "y". C'est ce que j'ai écrit sur l'image.
Seulement voilà, j'ai écrit cette équation afin d'en avoir une pour enfin la manipuler dans le sens que je veux. Et c'est là qu'il y a l'os.
Ce qui m'intéresse ce n'est pas de calculer "y" puisque dans mon cas il est connu.
A vrai dire, je connais "y", "a" et "d". Mais l'inconnu est "e". Je voulais trouver une formule qui me donne la longueur "e" en fonction des 3 autres.
Alors avec la formule que j'avais sur le papier, j'ai essayé d'isoler "e" mais il se trouve dans deux racines différentes, et là je sèche...
Autre point, j'ai essayé de traiter ce problème de manière différente en utilisant la trigonométrie à la place de Pythagore, mais le problème est sensiblement équivalent puisque j'avais obtenu cette équation :
alpha1 = acos(a/e)
alpha2 = acos(a/(e+d))
v = a*sin(alpha1)
w = a*sin(alpha2)
y=v-w
donc :
y=a*sin(acos(a/e))-a*sin(acos(a/(e+d)))
Pour arriver à extraire "e" de cette formule je suis également largué.
Pour l'instant, je ne peux résoudre ce problème que de manière empirique ou expérimentale ce qui prend du temps, j'aurais aimé avoir une formule que je mets dans un programme sur la calculatrice qui me sort "e" juste en entrant "a", "y" et "d".
Je préviens tout de suite que ça n'est nullement un travail pour l'enseignement. C'est 100% personnel.
Pour ceux qui veulent savoir à quoi ça sert : à vrai dire une telle formule me permettrai de dessiner un valve-gear stephenson avec énormément de précision et immédiatement sans avoir recours aux essais pour ajustage. Ca peut aussi servir à d'autre problèmes similaires
Je vous remercie par avance.
-----