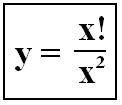Bonjour/soir,
Comment prouver que :donne tous les nombres premiers? (lorsque n décrit
De même pour:
(et cette fois si elle est injective en plus!)
Source: http://www.cnrs.fr/Cnrspresse/math2000/pdf/Maths10.pdf
Mais je ne trouve aucun article avec une démo.
Merci par avance.
Bonjour, à mon avis vu que ces formules sont toutes jeunes, moins de 20 ans, si tu trouves un article qui te démontre la propriété de ces fonctions alors je doute que tu comprennes plus loin que la deuxième ligne... et moi par ailleurs.
C'est dommage. Surtout que je n'arrive même pas à voir pourquoi la première est toujours entière
Ben utiliser des parties entières déjà corse énormément la compréhension des résultats, en plus en faire une somme puis un inverse etc... pas facile.
Je parlais de la première formule, et il n'y a pas de partie entière.
Et les crochets ne sont là que pour faire joli ...? D'ailleurs il n'y a pas un erreur? (n+2)/p-(n+1)/p me semble simplifiable...
Oui, je parle de la première!
Je ne comprends d'ailleurs pas pourquoi ils n'ont pas retrancher les 2 fractions, pour avoir juste du 1/p au dénominateur.
Et si ! Dans la première formule (dans la deuxième aussi) les crochets indiquent bien la partie entière (et il t'en manque) , la formule exacte est :
L'explication (simplissime) peut se trouver ici : http://www.lifl.fr/~wegrzyno/FormulP...Premiers5.html
Merci bienEnvoyé par erik
Et si ! Dans la première formule les crochets indiquent bien la partie entière (et il t'en manque) , la formule exacte est :
L'explication (simplissime) peut se trouver ici : http://www.lifl.fr/~wegrzyno/FormulP...Premiers5.html
En fait oui c'est tout bête, j'en avait même faite une moi même! Une pour la fonction pi qui compte les nombres premiers sous forme de somme mais très peu intéressante car au pire équivalente en niveau de calcul à un algorithme simple. Ce juste en remarquant que E(E(m/n)n/m) est égal à 1 ou 0 suivant si n divise m ou pas
Bonsoir,
Grossièrement, je dirais : la somme du dénominateur compte les nombres premiers plus petits que m (théorème de Wilson), et on remarque que la somme totale contient des termes qui s'annulent pour m suffisamment grand donc on a pas besoin de s'inquiéter de la borne, il suffit de la choisir suffisament grande. La somme pourrait donc se réécrire comme
Ce n'est pas tout à fait le résultat recherché, mais l'idée doit y être, il faut ensuite écrire tout ça proprement (il doit être plus facile de partir de la fin du raisonnement).
If your method does not solve the problem, change the problem.
Merci, en effet, il y a certainement du Wilson. Comment justifiez-vous la borne 2^n ?
La borne b(n) doit être telle qu'il existe au moins n nombres premiers inférieurs à n. Or d'après le postulat de Bertrand, pour tout n>2, il existe au moins un nombre premier compris strictement entre n et 2n. Par récurrence, on montre donc que b(n)=2n convient.
If your method does not solve the problem, change the problem.
Ah oui, je n'y avais pas pensé... (la preuve d'Erdos de ce "postulat" est d'ailleurs très élégante).
Cette formule est bien compliquée. Je m'intéresse seulement à (j-1)!/j, en simplifiant j!/j^2
Si j est premier, alors le résultat n'est pas entier. (exception j=4)
Pour plus d'explications: https://remy.veritis.ch/accueil/
Bonjour.
Dommage de commencer (premier message) par une grossière erreur de logique ("exception j=4").
Mais comme ce n'est qu'une pub pour ta page personnelle, ça n'a finalement que peu d'intérêt. Et ne répond pas au sujet.
Pour les autres lecteurs : C'est une évidence de débutant en arithmétique que le produit des entiers strictement inférieurs à un premier p n'est pas divisible par p.
Dernière modification par gg0 ; 22/09/2024 à 18h41.
