Bonjour à tous,
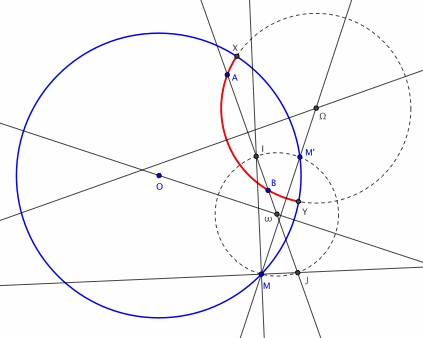
Je me demandais : Si l'on se donne deux points dans le disque de Poincaré, comment construire la géodésique passant par ces deux points ?
Autrement dit : Si l'on se donne un cercle et deux points à l'intérieur de celui-ci, comment construire un cercle passant par ces deux points et intersectant le premier cercle perpendiculairement ?
Seirios
If your method does not solve the problem, change the problem.
Bonjour,
Le cercle à construire, passant par A et B, fait partie du faisceau à point de base A et B, et son centre Ω est sur la médiatrice du segment [AB], c'est l'intersection de cette médiatrice avec l'axe radical du cercle donné et d'un cercle quelconque du faisceau à points-limite A et B.
On se donne un point M du cercle donné, le cercle du faisceau à points-limite A et B passant par M admet pour diamètre porté par la droite (AB) le segment [IJ] dont les extrémités sont les pieds des bissectrices des angles en M du triangle AMB. On construit donc facilement les points I et J, puis le centre ω du cercle cherché. L'axe radical de ce cercle avec le cercle donné est la perpendiculaire abaissée du point M sur la droite (Oω), ce qui fournit le point Ω. La géodésique est l'arc XY du cercle de centre Ω passant par A et B.
Annulé... Inutile.
Pour toute question, il y a une réponse simple, évidente, et fausse.
Merci God's Breath pour cette réponse !
If your method does not solve the problem, change the problem.
