loi uniforme

[kaderben]

Bonjour
Voici un exo sur la loi uniforme
Sur une voie unique, un feu de signalisation:
il clignote pendant 2 minutes et les voitures passent
puis il passe au rouge pendant 1,5 minutes et les voitures s'arrêtent (en attente de passer).
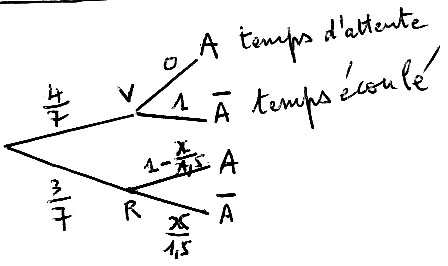
1°) probabilité que la voiture arrive au feu alors qu'il clignote ?
2°) On considère la variable aléatoire T " temps d'attente au feu"
Déterminer P(T=0) et P(T <= x) pour x dans ]0;1,5]

Réponse
1°) P( clignote ) = 2/3,5 = 4/7
2°) Même avec la correction je n'ai rien compris.

La correction suggère une variable aléatoire X égale au temps écoulé (en min) du début à la fin d'un cycle "clignotant , attente"
donc X uniforme sur [0 ; 3,5]
J'ai fait le dessin suivant mais cela ne m'inspire pas grand chose
<______________X_________>
<_____Clig_____><____T____>

0-----------------2-------------3,5

Clig = Tbarre
Eventuellement, je peux poster la correction si besoin
Merci pour vos commentaires
-----

[gg0]

Bonsoir.

Examinons concrètement les choses :
T=0 signifie que l'automobiliste arrive à un moment ou le feu clignote. Donc tu as déjà calculé cette probabilité.
Pour x>0, T n'est pas nul, donc en modélisant par une variable uniforme :
P(0<T<=x)=P(T#0 et T<=x)=P(T#0)*P(T<=x/T#0)=3/7*(1,5-x)/1,5
Le 1,5-x est le temps d'attente quand on arrive x mn après le passage au rouge, (1,5-x)/1,5 est le rapport entre le temps au rouge et le temps d'attente, qui est, loi uniforme oblige, la probabilité d'attendre ce temps là.

Est-ce que ça éclaire ta lanterne ? Ou es-tu encore au rouge en attente ?

Cordialement.

[kaderben]

Bonjour gg0
Ton raisonnement est simple mais ça ne colle pas avec les réponses du livre.
Il faut dire que je trouve plein d'erreurs de frappe et aussi de raisonnement dans les réponses du livres.
Ci joint le corrigé

corrig&#233;1.jpg
corrig&#233;2.jpg

[gg0]

Le corrigé a raison.

J'ai utilisé pour x non le temps d'attente, mais le temps écoulé depuis le passage au rouge. Donc mon 1,5-x est à remplacer par x, et les deux méthodes coïncident (ne pas oublier de rajouter le P(T=0)).

Cordialement.

[A voir en vidéo sur Futura]

[kaderben]

Bonjour ggO
Après un si long temps, je voulais reprendre si tu ne vois pas d'inconvénient
1°) C'est toi qui a calculé la proba du temps d'attente demandé et non l'auteur du corrigé.
Tout simplement, si une voiture arrive après x minutes aprè passage au rouge, le temps d'attente est bien 1,5 -x, et tu as utilisé que la variable aléatoire T qui est le plus simple à mon avis.
Tu as raisonné comme ceci:
la voiture arrive au feu vert (proba=4/7) ET elle attend (proba = 0) OU elle n'attend pas (proba=1)
OU
la voiture arrive au feu rouge (proba=3/7) ET elle attend (proba = (1,5-x)/1,5) OU elle n'attend pas (proba=x/1,5)
attend:temps d'attente
n'attend pas :temps écoulé

2°) le corrigé nous embrouille avec les deux variables aléatoires X et T
finalement l'auteur a calculé la proba de lévénement contraire, proba du temps écoulé après le passage au rouge.

Voici un arbre pour résumer la situation



P(T>x) P(x<T<1,5)= P(A) = 4/7*0 + 3/7( (1,5-x)/1,5 = (3-2x)/7, c'est ce que tu as trouvé

On vérifie bien que (3-2x)/7 + (4+2x)/7 = 1

Je ne garantie rien mais je pense que c'est ça

Merci pour les commentaires

[gg0]

Non, non,

le corrigé a bien raison.
Le temps d'attente est au plus 1,5 et on doit avoir P(T<=1,5)=1. Et aussi P(T<=0)=4/7. La formule P(T)= (4+2x)/7 est la bonne.

Cordialement.

NB : la difficulté ici est que T diminue dans le temps d'un feu.