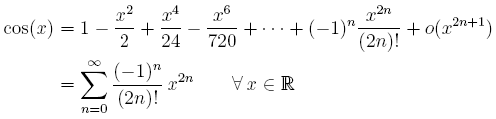calcul mental du cosinus

[invited6c27078]

Bonsoir,
J'aimerais savoir comment on sait que:
cos(x ) = sum[ (-1)ⁱ / (2i)! x⁽²ⁱ⁾ ] pour i allant de 0 a n
Qu'est ce que "sum" et x⁽²ⁱ⁾
Je crois que pour trouver la valeur approchee de cos(1), par ex, il faut faire:
1er terme:
quand i=0, on a:
(-1)ⁱ=(-1)⁰= 1
et (2i)!=(2*0)!=0!= 1
D'ou on a: 1/1 = 1

2eme terme:
quand i=1, on a:
(-1)ⁱ=(-1)¹= -1
(2i)!=(2*1)!=2!=2*(2-1)=2
D'ou on a: -1/2

3eme terme:
quand i=2, on a:
(-1)ⁱ=(-1)²=1
(2i)!=(2*2)!=4!=4(4-1)(4-2)=24
D'ou, on a: 1/24

et ainsi de suite, si on veut plus se raprocher de la realite...

Donc, pour une approximation de cos(1) a 1/24, on a:
cos(1)=1-1/2+1/24 .....

Cependant, on utilise pas "x⁽²ⁱ⁾ " a quoi ca sert?
Au faite, sum, c'est parce que l'on doit additionner les termes?
Merci d'avance
a+
PS: Pourquoi 0!=1?? si l'on fait 0(0-1) on a 0 non?...
-----

[matthias]

Cependant, on utilise pas "x⁽²ⁱ⁾ " a quoi ca sert?

C'est x à la puissance 2i, comme tu as pris x = 1, que tu le fasses apparaitre ou non, ça ne change pas grand-chose effectivement.

Au faite, sum, c'est parce que l'on doit additionner les termes?

Oui, sum = somme en anglais

PS: Pourquoi 0!=1?? si l'on fait 0(0-1) on a 0 non?...

C'est une convention bien pratique et dont la cohérence apparait dans ce genre de formules.

Pour la démonstration de la formule, il faudrait d'abord nous dire quel est ton niveau pour voir si c'est abordable.

[invited6c27078]

Merci de ta reponse,
alors, pour le niveau, c'est sur que ca ne va pas etre abordable... (1^èreS et non pas SUP bien sur)
Par contre, on m'a montre cette méthode, et elle est bien pratique, pour les choses simples en tout cas.

C'est x à la puissance 2i, comme tu as pris x = 1, que tu le fasses apparaitre ou non, ça ne change pas grand-chose effectivement.

Ok, et si je voulais calculer le cosinus de (2) par exemple, je remplace x par 2 c'est bien ca?
et donc, là, cos(x ) = sum[ (-1)^i / (2i)! x⁽²ⁱ⁾ ]. C'est "(2i)! * x⁽²ⁱ⁾ " ?? ou .... c'est juste + x⁽²ⁱ⁾
Merci d'avance
a+

[invite77a86db2]

Le calcul dont tu parles est issu des développements limités.
Pour tout mettre de façon claire, tu as ceci :

Où le symbole bizarre avec n=0 en dessous et l'infini au dessus est le symbole de la somme des termes.
Si tu as déjà programmé, c'est une simple boucle, on prend n=0 au départ, on remplace n par 0 dans la formule, on stocke le résultat, et on incrémente n. On remplace alors n par 1 dans la formule, on ajoute le résultat au résultat précédent, et on recommence...

Pour ta question sur la factorielle :
http://fr.wikipedia.org/wiki/Factorielle

[A voir en vidéo sur Futura]

[GuYem]

Dans ce cas on n'utilise pas x^2i parce que x=1. Et à la puissance bidule ça fait 1. D'autre part je ne crois pas que ce soit trop une bonne méthode pour donner une approximation de cos. Vaut mieux prendre une calculatrice

Et puis 0! ça fait 1 presque par convention.

[invited6c27078]

ok, merci beaucoup, j'avais deja vu ce symbole bizar qqpart (j'ai oublie son nom...)
Par contre, c'est une formule que l'on peut utiliser sans demonstration?
Merci d'avance
a+

[invite77a86db2]

Euh, de quelle formule tu parles ?
Tu veux démontrer le signe égal ?
Je te dis, ce sont les développements limités, mais en 1ère S, tu n'as pas réellement le niveau pour tout voir à ce sujet crois-moi

[invited6c27078]

D'autre part je ne crois pas que ce soit trop une bonne méthode pour donner une approximation de cos

Oui, j'aurais prefere prendre la calculatrice, mais on doit trouver une valeur approchee par defaut de cos(1) a 1/24 pres, donc avec ca, j'ai cos(1)=1-1/2+1/24 et de la je peux en deduire que 1-1/2 "à peu pres egal à" 1/24, d'ou une approximation par defaut de cos(1) a 1/24 pres... non?
Ou je me suis completement trompe, et ce n'est pas comme ca que l'on calcul une valeur approchee d'un cosinus (mentalement)...
Merci d'avance
PS:

tu n'as pas réellement le niveau pour tout voir à ce sujet crois-moi

Oui, je le sais très bien, mais on m'a montrer ca pendant les vacances, et je croyais que je n'aurais pas besoin de m'en servir, mais la je ne vois pas comment faire autrement...