Bonjour tout le monde.
Il y a quelque semaine en arrière, j'ai réalisé ce graphique parce qu'il me semble être logique.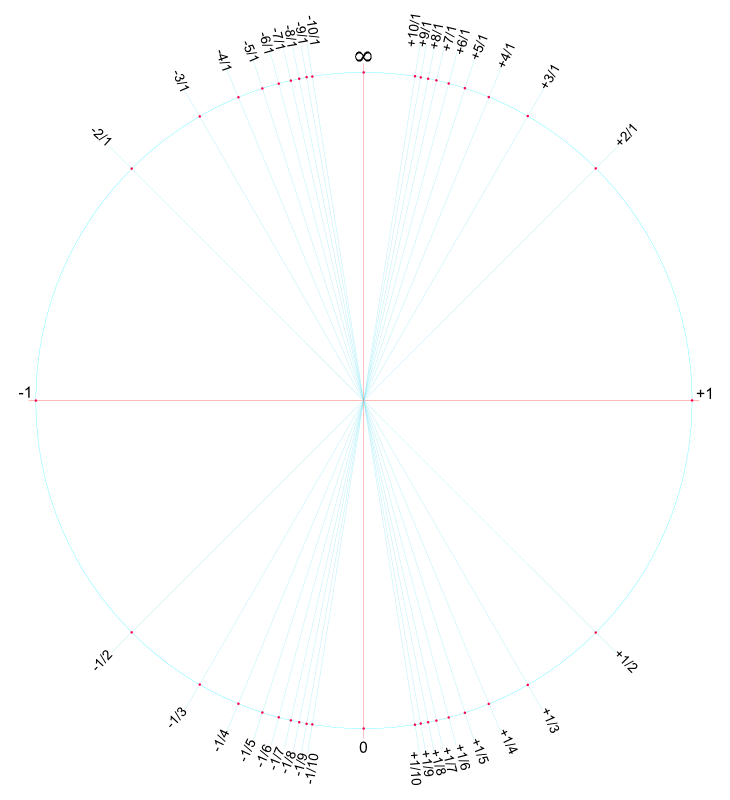
j'aimerais avoir votre avis.
merci
-----


Bonjour tout le monde.
Il y a quelque semaine en arrière, j'ai réalisé ce graphique parce qu'il me semble être logique.
j'aimerais avoir votre avis.
merci

Bonjour,
Difficile de vous donner un avis sur un graphique alors que vous ne donnez aucune information sur la façon de le construire ni sur sont interprétation.
On peut néanmoins noter que votre cercle tel que vous le représentez n'est autre que le compactifié d'Alexandroff de IR.
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse


En faite, je suis parti de l'idée que "1" ne peut être plus proche de "0" que de "l'infini" et j'ai voulu le représenté graphiquement.
ensuite je me suis poser la question suivante:
Ce graphique a t'il un rapport avec la relativité général?


Et puis, j'ai aussi remarqué que le graphique démontre qu'il y a une fonction inverse des mathématiques (en partant de "l'infini" vers "0").

Comme l'a dit Médiat, tu as simplement représenté la droite réelle comme un sous-espace du cercle, il n'y a pas grand chose à ajouter...
If your method does not solve the problem, change the problem.

1 :non ça ne démontre rien (un joli dessin ce n'est pas une démonstration)
2 :'il y a une fonction inverse des mathématiques" : ça ne veut absolument rien dire !

Bonjour,
Voulez vous dire que l'espace des réels entre l'infini et 1 n'est pas plus grand que celui entre 1 et 0 dans R car ils sont tout 2 infini ?
J'aurais tendance à le penser aussi, quel est la position officielle ?


Je vous propose ce dessin:
E til existe bien des fonctions inverse en mathématique , la preuve:http://fr.wikipedia.org/wiki/Fonction_inverse

Bonjour
Il y a deux réponses :
Oui (si on parle du cardinal)
et
Non (si on parle de la mesure usuelle)
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse


Oui, vous avez compris ou je voulais en venir. merci Médiat pour la réponse
Pouvez vous m'expliquer qu'elle est la différence entre cardinal et mesure usuel?

Bonjour,
Ces dessins sont censé prouver quoi exactement?


Oui c'est tout à fait ca, et c'est là que la relativité entre en jeu... (enfin je pense)


par exemple: en fonctions croissante 1+1=2, et en fonctions décroissante 1+1=0,5
pour MissPacMan
En faite, dans la fonction décroissante, il suffit d'inverser numérateur et dénominateur.


Pour être plus explicite, je pense que 0=infini et que ce n'est qu'une question de point de vue (relativité).

Pour le cardinal, c'est très simple, c'est juste une classe d'équipotence ; pour la mesure, c'est un peu plus compliqué, mais vous pouvez regarder ce document : http://www-fourier.ujf-grenoble.fr/e...tegrationa.pdf.
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse

Il vous faudrait donner un sens mathématique à une telle affirmation (en particulier, je ne vois pas comment le nombre réel 0, pourrait être égal à l'infini qui n'est pas un réel) ...
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse


Et j'avais encore une question par rapport au graphique: Ne peut t'on pas dire que (0/1).(1/0)=1 ???


Et bien je pense que 0 n'est pas plus réel que l'infini (ne le prenez pas mal, mais sa me semble évident)
Par exemple, en fonction inverse c'est l'infini qui devient réel et 0 devient irréel.

C'est bien sympa d'avoir des "impressions" comme ca, mais ca n'en fait pas des maths, loin s'en faut.



Ben je vois aps vraiment de question dans ce que tu dis.
Effectivement comme te l'a dit Médiat, on peut compactfier la droite réelle en rajoutant un point, et on obtient un cercle, par contre on perd toute la structure algébrique de la droite.
Effectivement le cardinal de ]0,1[ est le meme que celui de ]1,+oo[, ils ont le meme "nombre d'elements, ces deux espaces se ressemble beaucoup, ils sont meme impossible a discerner d'un point e vue topologique, c'est a dire que l'on peut déformer l'un en l'autre et l'autre en l'un sans probleme. C'est aussi le cas de ]12; 77[ et ]racine de 2, pi[, et en fait tout inervalle de la forme ]a,b[ avec a<b.
Ca ne veut pas dire que 0 et l'infini sont la meme chose, en fait, ca ne veut rien dire de profond du point de vue algébrique.

En essayant de mettre un peut d'ordre dans tout ça :
L'application inversepeut se prolonger par continuité sur la compactification d'Alexandroff (qui est homéomorphe au cercle)
, de telle sorte que
et
.
C'est une manière d'interpréter les graphiques. Maintenant, dire queet
sont "semblables" implique de dire que chaque
est "semblable" à
. Donc il n'y a rien de vraiment spécifique à
et
.
Qui plus est, un fois sur le cercle, il n'y a pas vraiment de différence entre les tous les points.
If your method does not solve the problem, change the problem.


Merci pour ta réponse misspacman.
Merci à toi aussi Seiros

Perplexe, c'est a dire?


Donc d'après vous, le graphique n'a aucun rapport avec la relativité?
Parce que, j'avais penser que peut-être, le graphique représente une dimension espace-temps avec l'espace à la verticale et le temps à l'horizontal.
Mais bon, je vais pas trop vous embêter avec mes questions et encore merci pour vos réponse.
Ciao

Je pense que tu n'embetes personne, rassure toi
Non, il n'y a pas de rapport entre ton graphique et la relativité.
La relativité est bien comprise, y a plus trop vraiment de mystere, je doute que tu puisse apporter qqch de nouveau d'une manière aussi simple.

Bonjour,
Comme on connait la mesure usuelle qui est la distance entre 1 et 0 : 1-0=1
Et que vous savez qu'il y a un espace infinis entre 0 et 1
Alors le cardinal est cet espace infinis
Je ne comprend pas pourquoi vous posez la question car je ne vois pas d'autres solution


Je t'avous qu'en plus j'ai développé tout ca en partant de mes recherches sur l'Hermétisme, la kabbale, etc... donc, c'est pour ca que je ne comprenais pas trop tout ca.

Il y a bien une différence de distance entre l'infini et 1 c'est une distance infinie
alors qu'elle est finis pour n'importe quel couple de réel dont 0,1
On ne pas pas dire que ce sont les mêmes espaces, il y a des borné complet (a,b), à droite R+, à gauche R- et pas du tout R


Est-ce juste de dire que en fonction inverse, la distance entre 1 et infini : 1-infini=1

