Moyennes par les racine énieme

[inviteb6b93040]

Bonjour,

Dans un autre fil l'idée HS m'est venue d'une moyenne par multiplication des valeurs suivie d'une racine énieme du nombre de ces valeurs

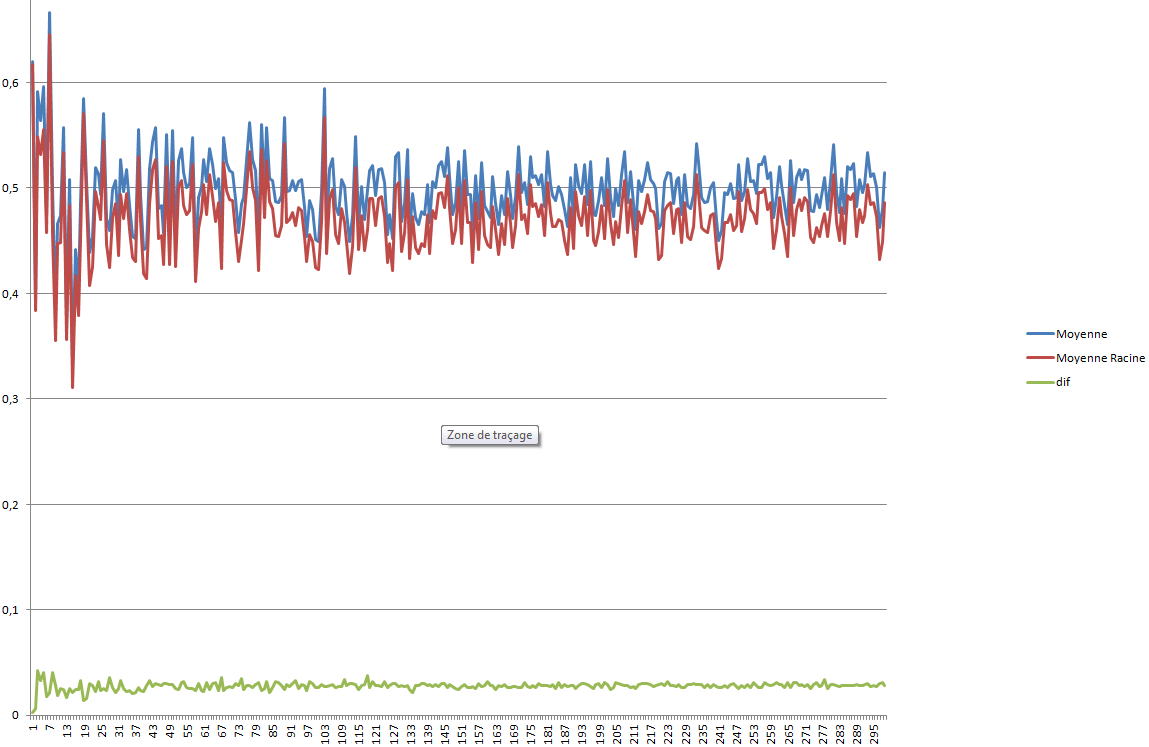
Constatant que pour 100 tirages aléatoires la moyenne classique n'était pas égale à la moyenne racine
J'ai voulue en savoir plus mais cette différence persiste et varie un peu comme l'écart à la moyenne !
Un mateux peux il m'expliquer cela ?

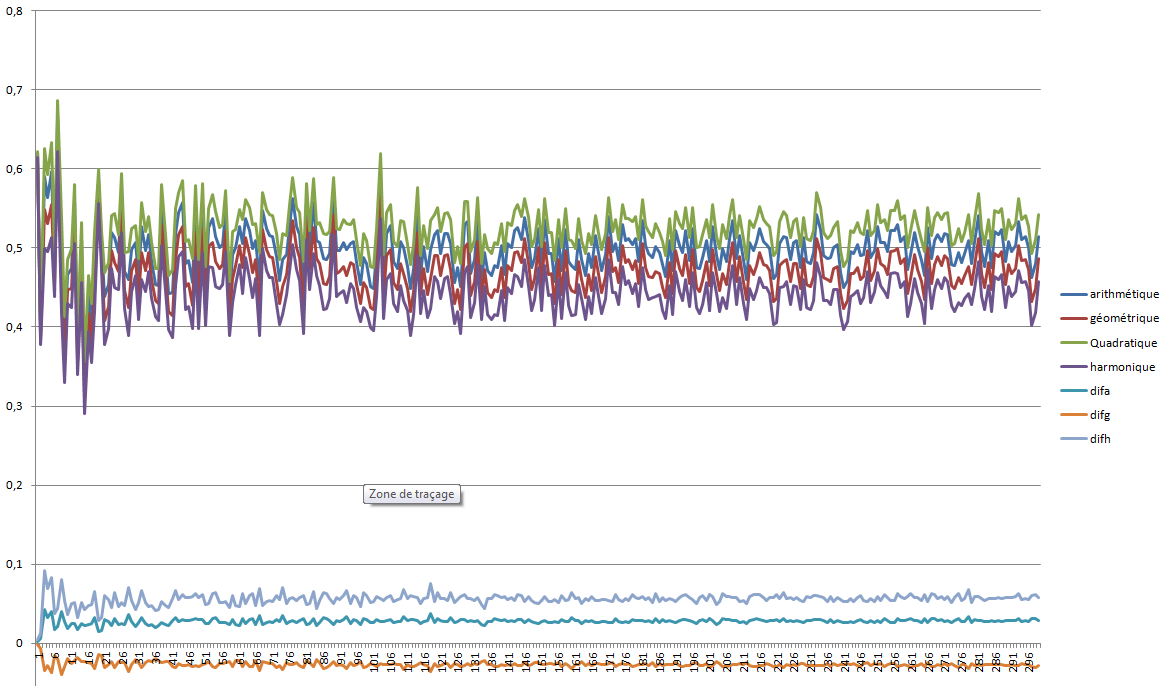
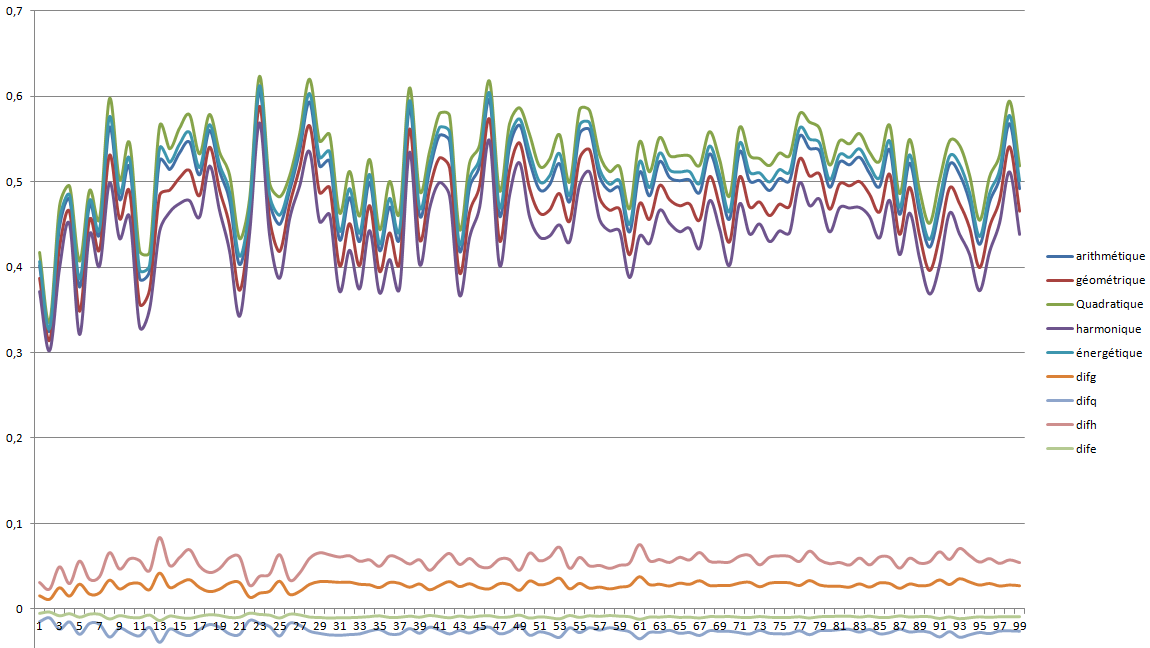
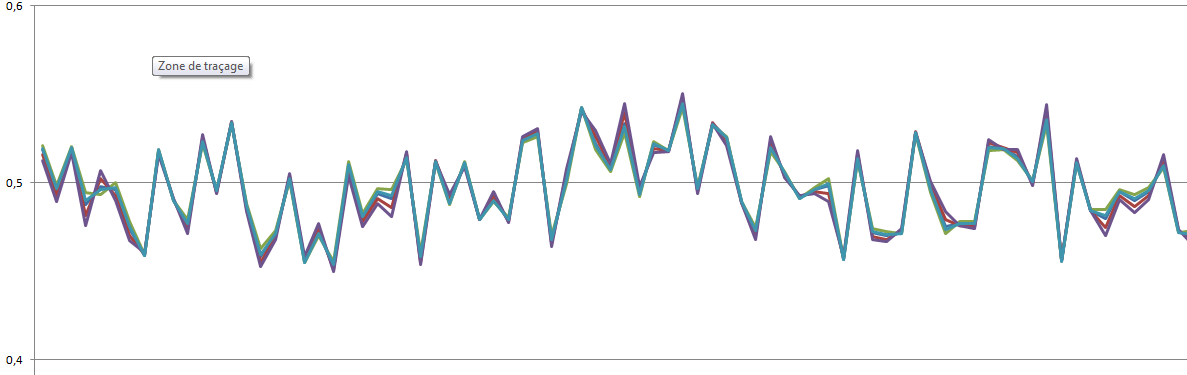
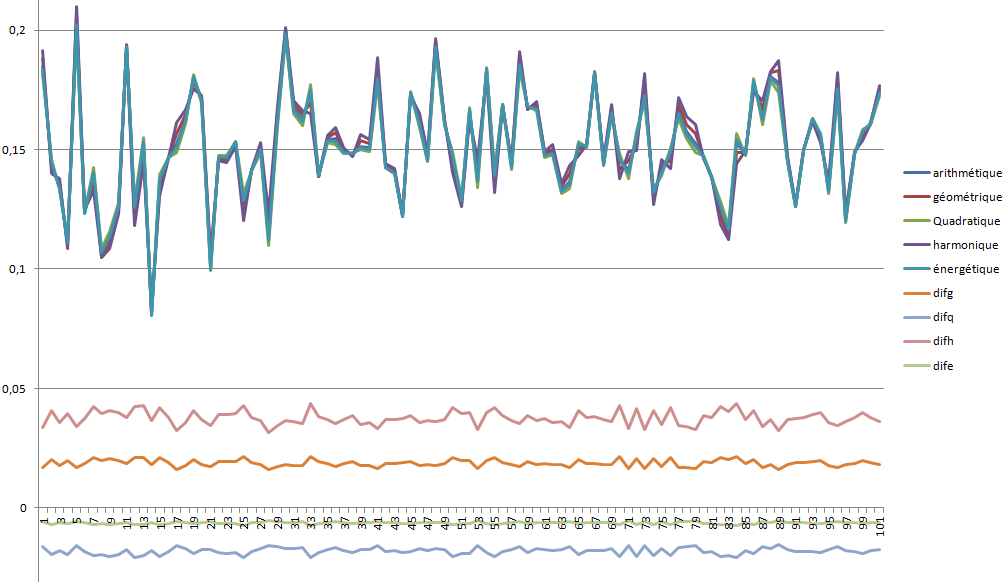
Voila les courbes de n = 2 à 300 tirages aléatoires


et le code VBA qui génère les données

Function Moyennes()
    ch = "D:\MSVCNT\pianoVB\"
    Open ch & "Moyennes.csv" For Output As 1
    Print #1, "Nombre;Moyenne;Moyenne Racine;dif"
    For n = 2 To 300
        m2 = 1
        m1 = 0
        For I = 1 To n
            g = Rnd() + 1
            m1 = m1 + g
            m2 = m2 * g
        Next I
        m11 = m1 / n
        nn = 1# / n
        m22 = m2 ^ nn ' prend la racine énième
        Print #1, n & ";" & m11 - 1 & ";" & m22 - 1 & ";" & m11 - m22
    Next n
    Close #1
End Function

-----

[sylvainc2]

Ca s'appelle une moyenne géométrique:

http://fr.wikipedia.org/wiki/Moyenne...om%C3%A9trique

[Médiat]

Bonjour,

La moyenne géométrique que vous proposez est l'exponentielle de la moyenne arithmétique du logarithme des valeurs observés.

Vous auriez-pu ajouter à vos calculs et graphes :

La moyenne harmonique
La moyenne quadratique
La moyenne énergétique

[inviteb6b93040]

Bonjour
Merci, c'est plus simple avec le logarithme
Je découvre aussi comment elle est utilisé dans votre lien
Mais pourquoi elle est différente de la moyenne arithmétique et sa différence semble suivre l'écart à la moyenne ?

Pour les statisticiens, la moyenne géométrique (antilogarithme de la moyenne des logarithmes de chacune des observations) est moins sensible que la moyenne arithmétique aux valeurs les plus élevées d'une série de données. Elle donne, par conséquent, une autre et meilleure estimation de la tendance centrale des données dans le cas d’une distribution à longue traine à l’extrémité supérieure de la courbe (type de distribution fréquente dans les mesures sanitaires ou environnementales par exemple de toxiques dans l'organisme le sang ou l'environnement, où certains individus ou groupes vulnérables ou exposés à des cas particulier sont plus affectés).

[A voir en vidéo sur Futura]

[inviteb6b93040]

Bonsoir

Vous auriez-pu ajouter à vos calculs et graphes :

La moyenne harmonique
La moyenne quadratique
La moyenne énergétique

Faites votre choix la quadratique est la plus optimiste
Je n'ai pas fait la moyenne énergétique car je ne comprend pas bien la formule

Function Moyennes()
    ch = "D:\MSVCNT\pianoVB\"
    Open ch & "Moyennes.csv" For Output As 1
    Print #1, "Nombre;arithmétique;géométrique;Quadratique;harmonique;difa;difg;difh"
    For n = 2 To 300
        m2 = 1
        m1 = 0
        m3 = 0
        m4 = 0
        For I = 1 To n
            g = Rnd() + 1
            m1 = m1 + g
            m2 = m2 * g
            m3 = m3 + g * g
            m4 = m4 + 1 / g
        Next I
        m11 = m1 / n
        nn = 1# / n
        m22 = m2 ^ nn
        m33 = (m3 / n) ^ 0.5
        m44 = n / m4
        Print #1, n & ";" & m11 - 1 & ";" & m22 - 1 & ";" & m33 - 1 & ";" & m44 - 1 & ";" & m11 - m22 & ";" & m11 - m33 & ";" & m11 - m44
    Next n
    Close #1
End Function

[inviteb6b93040]

Bonjour,

Pour l'énergétique (m55) Il me manquait le log10 dans mon VBA mais j'ai trouvé comment le calculer avec le log

Function Moyennes()
    ch = "D:\MSVCNT\pianoVB\"
    Open ch & "Moyennes.csv" For Output As 1
    Print #1, "Nombre;arithmétique;géométrique;Quadratique;harmonique;énergétique;difg;difq;difh;dife"
    For n = 2 To 100
        m2 = 0
        m1 = 0
        m3 = 0
        m4 = 0
        m5 = 0
        For I = 1 To n
            g = Rnd() + 1
            m1 = m1 + g
 '           m2 = m2 * g
            m2 = m2 + Log(g)
            m3 = m3 + g * g
            m4 = m4 + 1 / g
            nn = g / 10#
            m5 = m5 + 10 ^ nn
        Next I
        m11 = m1 / n
        nn = 1# / n
 '       m22 = m2 ^ nn
        m22 = Exp(m2 / n)
        m33 = (m3 / n) ^ 0.5
        m44 = n / m4
        m55 = 10 * Log(m5 / n) / Log(10#)
        Print #1, n & ";" & m11 - 1 & ";" & m22 - 1 & ";" & m33 - 1 & ";" & m44 - 1 & ";" & m55 - 1 & ";" & m11 - m22 & ";" & m11 - m33 & ";" & m11 - m44 & ";" & m11 - m55
    Next n
    Close #1
End Function

[inviteb6b93040]

Bonjour,

Pour les musiciens curieux d'écouter les différentes moyennes formant un accord de 5 notes sur la suite aléatoire de mes courbes de 2 à 1000 (milles accords) en fichier midi
MoyennesMidi.zip
Et si vous êtes aussi informaticien
La fonction qui écrit les 5 moyennes par lignes lue par un séquenceur

Function Moyenne()
    ch = "D:\MSVCNT\pianoVB\"
    Open ch & "Moyennes.txt" For Output As 1
    For n = 2 To 1000
        m2 = 0
        m1 = 0
        m3 = 0
        m4 = 0
        m5 = 0
        For I = 1 To n
            g = Rnd() + 1
            m1 = m1 + g
 '           m2 = m2 * g
            m2 = m2 + Log(g)
            m3 = m3 + g * g
            m4 = m4 + 1 / g
            nn = g / 10#
            m5 = m5 + 10 ^ nn
        Next I
        m11 = m1 / n
        nn = 1# / n
 '       m22 = m2 ^ nn
        m22 = Exp(m2 / n)
        m33 = (m3 / n) ^ 0.5
        m44 = n / m4
        m55 = 10 * Log(m5 / n) / Log(10#)
        Print #1, Int(m11 * 10) & ";" & Int(m22 * 20) & ";" & Int(m33 * 30) & ";" & Int(m44 * 40) & ";" & Int(m55 * 50)
    Next n
    Close #1
End Function

[inviteb6b93040]

Bonjour

Les courbes avec l'énergétique sur 100
C'est la plus proche de l'arithmétique

[inviteb6b93040]

Bonjour,

Ne pourrait on pas rapprocher un peut mieux toutes les moyennes de la moyenne arithmétique ?

J'ai calculé le % moyen d'écart à la moyenne arithmétique sur 100 séries aléatoires

géo	quadra	harmonie énergie
1,85%	-1,79%	3,71%	-0,62%

Les fichier xls et midi car j'ai fait des accords et des notes

moyennes.zip

[inviteb6b93040]

J'ai refait un essaie de n=100 à 1000 pour voir comment les % de différence change

n		géométrique	Quadratique	harmonique	énergétique

100		1,90%		-1,83%		3,81%		-0,64%
1000		1,85%		-1,79%		3,71%		-0,62%

En décalant les courbe du % moyen de leur différence ça donne ça

[inviteb6b93040]

Avec une meilleure mise en page

Function RapInverse(r)
    RapInverse = 1 / (1 - r) - 1
End Function
Function Moyennes()
    ch = "D:\MSVCNT\pianoVB\"
    Open ch & "MoyennesC2.csv" For Output As 1
    Print #1, "Nombre;arithmétique;géométrique;Quadratique;harmonique;énergétique;difg;difq;difh;dife"
    rg = RapInverse(1.9 / 100)
    rq = RapInverse(-1.83 / 100)
    rh = RapInverse(3.81 / 100)
    re = RapInverse(-0.64 / 100)
    dy = 1.35
    For n = 100 To 200
        m2 = 0
        m1 = 0
        m3 = 0
        m4 = 0
        m5 = 0
        For I = 1 To n
            g = Rnd() + 1
            m1 = m1 + g
 '           m2 = m2 * g
            m2 = m2 + Log(g)
            m3 = m3 + g * g
            m4 = m4 + 1 / g
            nn = g / 10#
            m5 = m5 + 10 ^ nn
        Next I
        m11 = m1 / n
        nn = 1# / n
 '       m22 = m2 ^ nn
        m22 = Exp(m2 / n)
        m33 = (m3 / n) ^ 0.5
        m44 = n / m4
        m55 = 10 * Log(m5 / n) / Log(10#)
        Print #1, n & ";" & m11 - dy & ";" & m22 - dy + rg * m22 & ";" & m33 - dy + rq * m33 & ";" & m44 - dy + rh * m44 & ";" & m55 - dy + re * m55 & ";" & (m11 - m22) / m11 & ";" & (m11 - m33) / m11 & ";" & (m11 - m44) / m11 & ";" & (m11 - m55) / m11
    Next n
    Close #1
End Function