Bonjour à tous,
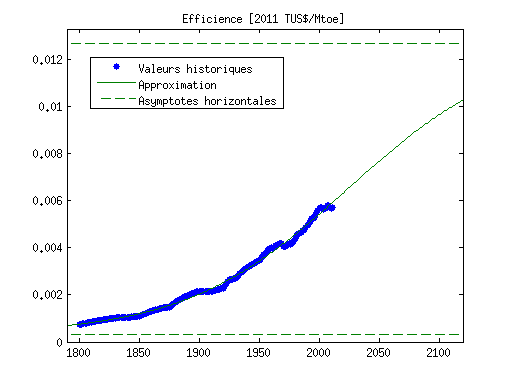
Pour la finalisation de mon travail de fin d'étude, je dois approximer une série de données, représentant l'efficience énergétique, c'est à dire le PIB divisé par la consommation énergétique depuis 1800 à nos jours. Sur l'image en pièce jointe l'on peut observer les valeurs à approximer représentés par des gros points bleus ainsi que la fonction qui approxime les données en vert. J'utilise pour ceci la fonction nlinfit sur MATLAB et comme fonction à approximer
Par contre, j'aimerais pouvoir donner un degré de liberté en plus à ma fonction analytique afin qu'elle approxime mieux mes points expérimentaux. C'est à dire qu'actuellement il y a une erreur d'approximation due à la symétrie parfaite de la fonction sigmoïde utilisée pour l'approximation. En effet, la fonction ci-dessus a son point d'inflexion pile entre les asymptotes horizontales supérieure et inférieure (en vert pointillé) de la fonction.
Et ceci n'est pas le cas de nos données expérimentales, on peut imaginer que le point d'inflexion se trouve un peu avant l'an 2000, mais cela ne nécessite pas à l'efficience d'augmenter encore d'autant que ce qu'il a déjà augmenté. En effet, cette efficience augmente historiquement avec les découvertes et il serait même logique qu'il y ait une augmentation qui ressemble à une exponentielle jusqu'à un point d'inflexion plutôt abrupte qui ramène la fonction rapidement en-dessous d'une asymptote supérieure ...
Ma question est donc la suivante, quelqu'un a-t-il une idée de la fonction que je pourrais mettre en approximation ? Une fonction qui a la même structure que celle ci-dessus mais qui laisse la liberté à mon approximation de monter ou descendre le point d'inflexion sans bouger les asymptotes horizontales.
Cette fonction aura bien évidemment un degré de liberté en plus (c'est à dire un 5ième paramètre).
Un tout grand merci pour votre aide et un très bel été !
Olivier
-----




