Bonjour à tous,
On peut trouver sur ce site le problème suivant :
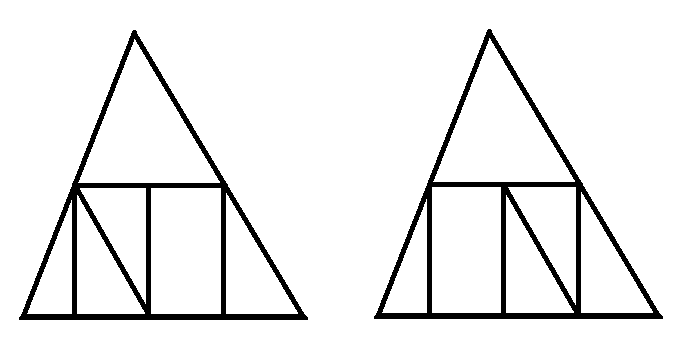
Je pense en avoir trouver une solution, que je joins à ce message. Pour que le raisonnement soit le plus clair possible, voici l'idée générale :On découpe un triangle en morceaux polygonaux. Puis, en translatant indépendamment chacun de ces morceaux, on reconstitue un nouveau triangle. Prouver que le nouveau triangle est un translaté du premier.
Cliquez pour afficher
Cela dit, je serais intéressé par d'autres solutions. En voyez-vous ? Je me disais qu'il était peut-être possible de s'en sortir avec quelques connaissances en théorie des graphes.
Seirios
-----





 ; par semi-cône, je pense à quelque chose de la forme
; par semi-cône, je pense à quelque chose de la forme