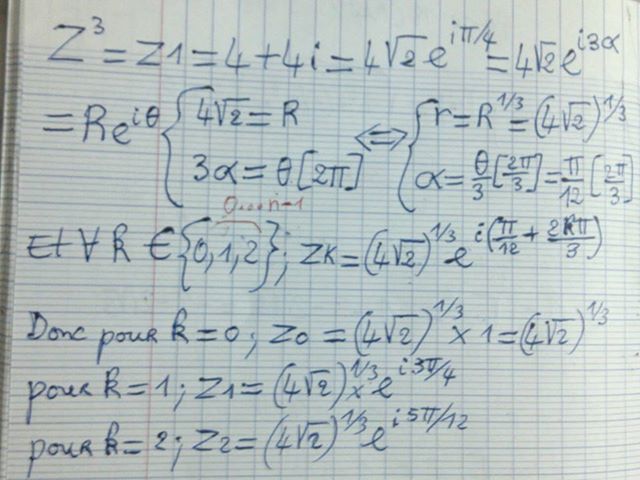complexe35

[Argon39]

Bonjour,j'ai créer cet exercice:
a)Résoudre dans C l'équation z³+8=0.
b)Donner la forme exponentiel de z.
c)calculer la racine cubique de z1=4+4i

Alors voici ce que j'ai fais:
a) (-2)³= -8 donc z= -2.
b) Puisque z=-2,alors z= 2*[EXP]iπ avec θ=π et |z|=2.
Ensuite pour le c):
La racine carré de z1= 4i+4= √(4i+4)=4√2*[EXP]iπ/8 avec z1=z² et 2θ=π/4.
Ensuite les racine nième de l'unité sont :
zk= [EXP]2ikπ/n avec k appartenant à {0,1,2}
z0=e^(0)=1
z1=[EXP]2ikπ/8=[EXP]iπ/4
z2=[EXP]4ikπ/8=[EXP]iπ/2
Mais vu que je ne vois pas qu'est que je peut faire avec ça je préfère changer de méthode.
Alors on a z1=4+4i ; |z1|=4√2 ensuite 3θ=π/4 d'ou θ= π/12+2kπ/3
Donc les racine cubique sont z1=4√2*[EXP]iπ/12 et z2=4√2*[EXP]i(π/12+2π/3) =4√2*[EXP](i3π/4) et c'est la même chose pour le dernier,z3=...
Mais cette méthode je l'ai vu sur le net et je me demande d'ou vien le "2kπ/3" du θ= π/12+2kπ/3, est ce que le 3 vient des mot "racine cubique"?(en gros je veu savoir pourquoi c'est pi/3 et non pi/4 ou...).
Merci.
-----

[Argon39]

J'ai essayer de mettre le symbole de l'exponentielle mais j'ai ça ma donner ça "EXP" en gros ça veut dire exponentiel,désolé.

[ansset]

pour la a) tu fais un raisonnement dans R , pas dans C !

[Argon39]

Oui je vois ce que vous voulez dire mais qu'est ce que j'aurais du écrire à la place?

[A voir en vidéo sur Futura]

[Argon39]

Bon déja on peut dire que z³+8=0 a comme racine évidente −2 mais il y a d'autres racine que je vais chercher d'ailleur.

[Argon39]

Bon alors pour la question a) j'ai compris,mais pour la c) Je propose autre chose:
c)z1=4+4i=4√2(cos(π/4)+isin(π/4)
Ensuite on peut dire que z³=z1=4+4i donc je peut écrire cela: (voir photo).

[ansset]

tu n'as pas fait le b).
d'autre part le c) demande la racine cubique, par la racine carrée. ???

[Argon39]

Pour la question a) on a z=-2 mais c'est une racine réel,on cherche les racine complexes nous donc on sait que z³+8=0 et quand on factorise ça on obtient:
(z+2)(z²-2z+4)=0 alors sont z-2= ou z²+2z+4=0 dans le premier ca z=2; et dans le deuxième c'est une équation du second degré et delta=-12 donc z1= 1-i √3 et z2=1+i √3.
Ensuite le module de z1=|z1|=|z2|= √4=2 et θ=π/3 pour z1 et θ=2π/3 pour z2 d'ou z1=2*expo(i*pi/3) ett z2=2*exp(i*2pi/3).

[ansset]

Pour la question a) on a z=-2 mais c'est une racine réel,on cherche les racine complexes nous donc on sait que z³+8=0 et quand on factorise ça on obtient:
(z+2)(z²-2z+4)=0 alors sont z-2= ou z²+2z+4=0 dans le premier ca z=2; et dans le deuxième c'est une équation du second degré et delta=-12 donc z1= 1-i √3 et z2=1+i √3.
Ensuite le module de z1=|z1|=|z2|= √4=2 et θ=π/3 pour z1 et θ=2π/3 pour z2 d'ou z1=2*expo(i*pi/3) ett z2=2*exp(i*2pi/3).

tu es sur ?
pour moi ton z2 = -1+irac(3) par l'inverse ! ( 2pi/3 n'est pas une bonne réponse )

[ansset]

pour le c) commence à écrire proprement
z1=!z1!exp(i*theta +2kpi) ( ne pas oublier le 2kpi avant de faire les divisions par n , n étant 2 ou 3 ou .. en fonction des racines recherchées )

[Argon39]

Dans l'équation du second degrés,le "b" c'est -2 donc -b=2 par conséquent on ne peut pas trouvé -1+iracine de 3

[Argon39]

Je posterais le c) ce soir en espérant qu'il ne sera pas trop tard en france,c'est dommage qu'il y ai un décalage horaire important.

[ansset]

Dans l'équation du second degrés,le "b" c'est -2 donc -b=2 par conséquent on ne peut pas trouvé -1+iracine de 3

tu n'as pas compris.
ce que tu ecrit :
2pi/3 correspond à -1+rac(3)i, donc n'est pas la bonne réponse, enfin !

la bonne réponse est 2pi-pi/3 soit 5pi/3 et non 2pi/3

[Argon39]

Mon z2 c'est ça z2=1+i √3. et non -1............

[ansset]

tu changes à chaque fois entre ton z1 et ton z2, je suis perdu.
appelles les comme tu veux , mais donnes les bonnes reponse dans C.
et regarde ce que celà donne sur un cercle trigo.
dans C sur une équation de ce type les solutions forment une symétrie.

[Argon39]

ensuite pour z2 ce n'est pas 2pi/3 mais c'est pi/3 cos=1/2 et sin=racine 3/2 .

[ansset]

je revient à un truc simple: ( visuel )
solutions : 1+/-rac(3)
donc le cos est postitif, ça ne peut être le cas pour 2pi/3

[Argon39]

l'argument de z2 c'est pi/3 car cos= 1/2 et sinus=racine de 3/2 et non je ne change pas de z1 ni de z2

[ansset]

l'argument de z2 c'est pi/3 car cos= 1/2 et sinus=racine de 3/2 et non je ne change pas de z1 ni de z2

si tu persistes à dire qu'une des solutions est 2pi/3 j'abandonne.
le cos de 2pi/3 est négatif .
tu persistes ?

[Argon39]

Vous devez avoir raison. j'ai déja admis que ce n'est pas 2pi/3 mais ce n'est pas vôtre 5pi/3 non plus c'est pi/3 car on a z2=1+iracine de 3/2 et ça a toujours été ça mon z2,je vous laisse calculer l'argument de z2,ce n'est pas 5pi/3.
cordialement.

[ansset]

Vous devez avoir raison. j'ai déja admis que ce n'est pas 2pi/3 mais ce n'est pas vôtre 5pi/3 non plus c'est pi/3 car on a z2=1+iracine de 3/2 et ça a toujours été ça mon z2,je vous laisse calculer l'argument de z2,ce n'est pas 5pi/3.
cordialement.

appelle le 5pi/3 ou -pi/3 , pour moi c'est la même chose.
ps: je n'ai pas nié que pi/3 était UNE des réponses, c'est l'autre ou ça va pas !

dans C, dans ce cas ;, il y a 3 reponses , d'accord ?

[Argon39]

Oui on est d'accord sur ça les réponse sont 2=exp...;z1 et z1 et une réponse dans R.

[ansset]

alors, bon courage et bonne note, si tu es si sur de toi !

[Argon39]

hééé non non je ne suis pas si sur de moi,vous allez m'abandonner en cours de route ?non si j'étais sûr de moi je ne serais pas en train de vous poser des questions.

[ansset]

ben si,
dessine un cercle trigo et tu verras que ton 2pi/3 ne tient pas la route.
bye!

[ansset]

d'autres poursuivront peut être!
tu ne peut pas en permanence refuter ce que je dis en en même temps me demander de rester à "t'aider"

[Argon39]

ça fais lontemps que j'ai vu que ce n'est pas bon pi/3. C'est vrai que 5pi/3 et pi/3 c'est le même angle,toute mes excuse,bon vu qu'il est tard dans vôtre pays je vais vous libéré si vous voulez aller dormir,t je vous donne rendez vous demain matin ou demain soir,entre temps j'aurais déja posté le c).
Bon pour conclure les racine complexes sont z1 et z2(il n'y a que deux racine complexe) et le "(z+2)=0 implique que z=-2 mais c'est un réel -2.
Mais qui a parler de devoir?

[ansset]

ça fais lontemps que j'ai vu que ce n'est pas bon pi/3. C'est vrai que 5pi/3 et pi/3 c'est le même angle,toute mes excuse,bon vu qu'il est tard dans vôtre pays je vais vous libéré si vous voulez aller dormir,t je vous donne rendez vous demain matin ou demain soir,entre temps j'aurais déja posté le c).
Bon pour conclure les racine complexes sont z1 et z2(il n'y a que deux racine complexe) et le "(z+2)=0 implique que z=-2 mais c'est un réel -2.
Mais qui a parler de devoir?

2 erreurs.
les solutions sont bien pi/3 et -pi/3 ( c-d-d 5pi/3) qui est différent justement de pi/3 ( angle opposé et non le même )

[Argon39]

oui c'est l'opposé en effet,et si on résume les solution sont z1= z1=2*expo(i*pi/3) et z2= z1=2*expo(-i*pi/3).
Bon je commence un peu le c) même si je n'orais peut être pas le temps te le terminé, alors dans le c),z1=4+4i donc |z1|=racine de32=4racine de2. Ensuite l'argument(l'angle) théta= pi/4,la je ne pense pas que je me suis tromper,mais c'est pour la racine cubique que les chose se complique,parce que je pensais que ce que j'ai écrit (voir photo) était bon.
Cordialement.

[ansset]

oui c'est l'opposé en effet,et si on résume les solution sont z1= z1=2*expo(i*pi/3) et z2= z1=2*expo(-i*pi/3).
Bon je commence un peu le c) même si je n'orais peut être pas le temps te le terminé, alors dans le c),z1=4+4i donc |z1|=racine de32=4racine de2. Ensuite l'argument(l'angle) théta= pi/4,la je ne pense pas que je me suis tromper,mais c'est pour la racine cubique que les chose se complique,parce que je pensais que ce que j'ai écrit (voir photo) était bon.
Cordialement.

ok, pour l'argument, je t'avais conseillé plus haut d'ecrire theta+2kpi avant division.
et là on doit diviser par 3 !