les différentielles (a une variable)

[invite277ed6f1]

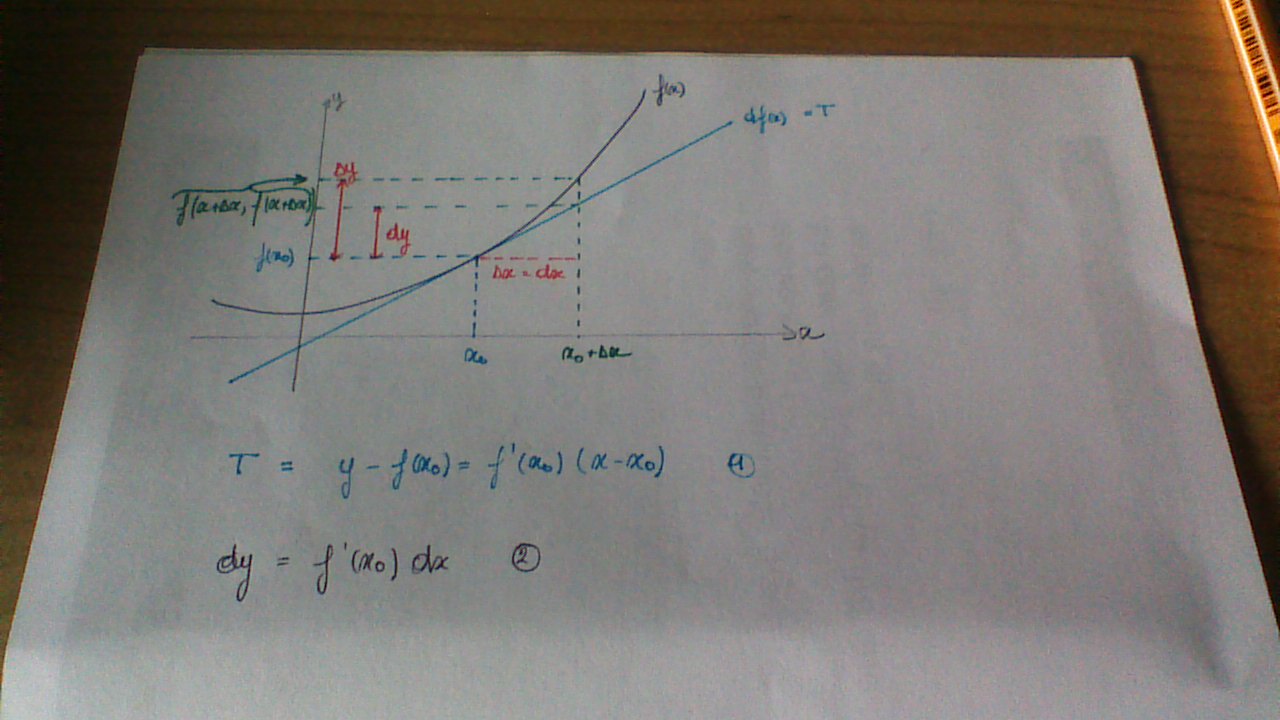
Bonsoir a tous, j'ai quelques petites question a propos des différentielles.

Tout d'abord cela m'a été expliqué avec un dessin que je suis ne peut pas vous envoyer pour le moment. Mais c'est le graphe banal ou l'on a une fonction f et sa tangente en un point x₀, on définit (delta) x, dx, dy et (delta) y
On connait l'equation de la tangente : y = f(x₀) + f'(x₀) (x-x₀)

Comment passer de cela a l'expression de la différentielle df = f'(x₀)dx ?
Et quelles est la différence ( théorique) entre la différentielle et la dérivée ?

Bonne soirée
-----

[gg0]

Bonjour.

je ne sais pas trop à quel niveau tu fais ça, ni pour quel usage. Tu trouveras facilement sur le net des documents parlant des différentielles et de leurs usages.
C'est essentiellement un outil de calcul, que tu peux considérer sans signification (formel). Il sert à idéaliser les quantités et lorsqu'elles sont extrêmement petites; et aussi à expliquer simplement les formules d'intégration par changement de variable. Il y a aussi une généralisation simple pour les fonctions de plusieurs variables.

Par contre, la distinction avec la dérivée est immédiate puisque la dérivée est f' (fonction dérivée) ou f'(x) (nombre dérivé), qui sert dans la définition de la différentielle.

A un autre niveau, on définira plus sainement la différentielle en x comme la fonction (linéaire) : de la forme avec a=f'(x) qui est donc constant (ce n'est pas x la variable, c'est dx). Mais comme souvent on confond la fonction avec une image quelconque (fonction x², par exemple), on appelle encore différentielle en x la quantité f'(x)dx.

Cordialement.

[invite277ed6f1]

Merci de votre réponse.

La formule des différentielles ne vient donc pas de l'équation de la tangente ?

[gg0]

Historiquement, oui.

Et elle a un lien, mais pour la tangente, il faut encore le point de tangence.
Au départ, dans la conception de Leibnitz, la courbe est conçue comme une succession de segments (comme ce que fait un traceur de courbes) "infiniment petits". La notion délicate d'infiniment petit est encore largement utilisée par les physiciens et ingénieurs, vu son caractère pratique, et a été remplacée en maths par le calcul des limites, avant de revenir, légèrement modifiée.
Donc pour Leibnitz, très près d'un point de la courbe de coordonnées (x,y), on a un point infiniment près (x+dx,y+dy) et la tangente est la droite déterminée par ces points? Sa pente est donc dy/dx=f'(x) et donc, comme pour lui, dx et dy sont des nombres, dy=f'(x) dx.
Cette idée très pratique a été contestée d'un point de vue conceptuel (c'est quoi ce dx qui n'est pas nul tout en n'intervenant pas dans des calculs quand on l'additionne ?), mais aussi technique (des calculs de ce genre peuvent donner des résultats faux dans certains cas). Quand on a un guide pour le résultat (comme dans la plupart des applications), c'est une excellente façon de présenter les calculs.

Cordialement.

NB : Lis un peu d'histoire des sciences et des maths, sur la période 16-ième/19-ième siécles.

[A voir en vidéo sur Futura]

[invite277ed6f1]

Ah merci bien

Je pensais comme les détracteurs de l'époque, j'ai du mal a concevoir que dx est un nombre.

Donc si je peux encore vous embêter deux minutes, quand je dessine le fameux schéma


Pour passer de l'équation 1 a la 2 je dois dériver ? Parce que dans ce cas, que devient le f(x0) ?

[gg0]

Je ne peux pas lire la pièce jointe pour l'instant,

mais je te le redis, la notion de différentielle peut être vue comme une notion formelle. Donc sans lien avec la tangente (autre que le fait que la différentielle a un rapport avec la dérivée, et la tangente aussi, par son coefficient directeur.
Une fois que tu as la définition dy=f'(x)dx lorsque y=f(x), tu as tout.
Et effectivement, dx et dy ne sont pas des nombres habituels(ils n'ont pas de valeur), mais peuvent permettre de faire du calcul approché (*). Mais il y a plein de choses qui ne sont pas des nombres et qu'on utilise en maths (les fonctions, les points, les droites, ...).

Je verrai ton document ultérieurement, mais à vue de nez, tu perds trop de temps sur une notion simple. Enfin, il faut voir quel usage en sera fait dans ta formation.

Cordialement.

(*) dans la théorie moderne des infiniment petits, ce sont des "nombres non standards", les nombres standards étant ceux que tu utilises.

[invite277ed6f1]

D'accord. Merci bien en tout cas.