Théorie de l'estimation

[Rids94]

Bonjour tout le monde :
j'ai une question concernant l'écart-type : pour une Population finie (Tirage sans remise) pour établir un intervalle de confiance on a m(+)ou(-) T(alpha) x Sigma/sqrt(n) x le facteur d'exhaustivité ----> bon ma question est la suivante : comment on estime l'écart type de la pop. mère ? en utilisant cette formule ?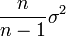
-----

[gg0]

Bonjour.

Si une formule (par exemple celle d'un intervalle de confiance) utilise , c'est à priori qu'il s'agit de l'écart type de la population, supposée connu.
Si cet écart type est inconnu, mais que la population est gaussienne, on peut utiliser la méthode de Student, où est remplacé par s (l'écart type d'échantillon, noté parfois ) et le coefficient de la loi de Gauss remplacé par celui de la loi de Student.

Mais comme je réponds avec seulement ce que tu as écrit, qui n'est pas particulièrement clair (*), tu peux éventuellement préciser la situation.

Cordialement.

(*) Je ne connais pas ta formule, qui me semble être une approximation.

[Rids94]

Je parle de cette formule et moi je veux calculer l'écart type de la pop mére à partir de l'écart type de mon échantillon

[Tryss]

Je parle de cette formule et moi je veux calculer l'écart type de la pop mére à partir de l'écart type de mon échantillon

Estimer, pas calculer

Dans ce cas, oui, L'écart type de l'échantillon multiplié par n/(n-1) est un bon estimateur de l'écart type de la population mère

Ah, j'avais pas fait gaffe au "sans remise" + "pop finie", dans ce cas un bon estimateur est



où N est la pop totale et n la pop de ton échantillon

[A voir en vidéo sur Futura]

[Rids94]

ah ok merci : ) apparemment j'ai confondu deux formules de deux cours différents , merci beaucoup bonne nuit