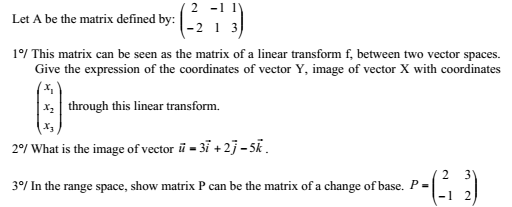Algèbre linéaire : changement de base

[ProCar]

Bonjour,

L’application lineaire qui intervient dans un changement de base est
l’identite, car on ne change rien aux vecteurs. On change seulement les
coordonnees des vecteurs dans une base.

Je ne comprends pas la phrase. Je veux dire, que vient faire la matrice identité ici ? Tout ce que je sais c'est qu'en la multipliant par une autre quelconque matrice elle redonne la matrice initiale.

Le but étant de comprendre comment opère-t-on des changements de bases et de coordonnées, sur lequel je suis en train de bosser.

Merci à vous !
-----

[ProCar]

Permettez moi de rebondir sur une autre question:

Dans la matrice de changement de base P, les colonnes sont les coordonnées des vecteurs exprimées de la nouvelle base exprimées dans l'ancienne base.

Mais les lignes correspondent à ...?

Merci !

[gg0]

Il ne s'agit pas de la matrice identité. Lis vraiment la phrase.
A priori, il a été précédemment défini la matrice d'une application linéaire (relativement à des bases données). C'est donc une application de ce cas général.

Pour la matrice de changement de base, on voit que les colonnes ont une signification. Un point c'est tout ! A priori, les lignes n'en ont pas.

Cordialement.

[untruc]

une base e_i, admet une base dite duale, noté, caractérisée par

c'est un produit scalaire, et le delta, c'est Kronecker.

si ta matrice de changement de base lie les bases et par

le vecteur ligne donne les coordonnées de dans la base .

alors les bases duales e_i^* et f_j^ sont liées par

donc, le vecteur colonne, c'est les coordonnés de dans .

si une base e est orthonormale, alors sa base duale est elle même.
Donc si j'ai un changement de base orthonormale vers orthonormale, alors on retrouve le résultat ou l'inverse d'une matrice orthonormale, est sa transposée.

Pour visualisez tous ca, va faloir que tu essayes de le faire en dimension 2. Mais je ne vois pas comment visualiser des matrices de changement de bases.

[A voir en vidéo sur Futura]

[untruc]

en fait si, prends e une base orthonormale (e_1, e_2)
sa base duale est elle même.

et considère f la base (f_1, f_2)= (e_1, e_1+e_2)
sa base duale est f^*=(e_2, e_1-e_2).

écrit la matrice de passage e vers f. Puis regarde la matrice de passage de f* vers e.

[ProCar]

Bonjour,

Je me permets de rebondir, puisque ma question est toujours sur le même sujet.



Je bloque à la question 3. L'image du vecteur u est '[-1 -19], mais je ne sais que faire pour montrer que P est une potentielle matrice de changement de base.

Merci pour votre aide !

[untruc]

P est inversible. c'est une matrice de changement de base dans R^2.