Bonjour à tous,
En régulation, je dois calculer 2 transformées de LaPlace de deux fonctions différentes :
1/
S1(t)=0 lorsque t<0
S1(t)=2t lorsque t compris entre 0 et 2
S1(t)=t+2 lorsque t>2
2/
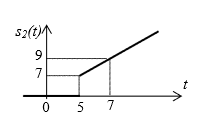
S2(t)=0 lorsque t<0
S2(t)=t² lorsque t compris entre 0 et 1
S2(t)=1 pour t>1
Comment dois-je procéder? Je sais juste que la fonction Heaviside va intervenir puisque je suis en régulation..
Quelqu'un pourrait-il m'aider? merci
Bonjour.
Dans les deux cas, tu écris ta fonction comme une somme ou différence de deux fonctions, produit d'une fonction simple par une fonction de heaviside pour l'annuler là où il faut. par exemple pour la première la fonction 2t lorsque t>0 peut s'écrire 2tY(t). Il suffit de lui rajouter une fonction convenable, nulle jusqu'à 2 pour avoir ce qu'il faut.
Essaie ...
Elle va intervenir mais pas n'importe comment.Envoyé par j-c57
En particulier, son argument doit être tel que la fonction soit causale. (sinon, c'est mort pour calculer la transformée de Laplace.)
Il est parfois tentant pour un débutant de faire des produits de fonction de Heaviside. Mauvaise idée en général car le calcul de la TL n'en est pas simple.
Donc pas de Y(-t) , pas de Y(t-t0).Y(t).
Juste des produits avec des fonctions de Heaviside retardée si besoin Y(t-t0) et des combinaisons linéaires comme signalé par gg0.
Cordialement.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Merci pour vos réponses.
Alors j'ai essayé et voici ce que je trouve:
Pour la 1/: Je suis pas vraiment certain, dois-je considérer un retard entre la fonction 2t et t+2 ?!
S1(t)=2tU(t) + t(U(t)(t+2)
S1(p)=(2/p^3)+(4/p²)
Pour la 2/:
S2(t)=t²U(t)
S2(p)=2/p^3
Ensuite j'ai un autre type d'exercice.. On me donne la courbe et il faut que je trouve sa transformée.
J'ai trouvé:
J'appelle To le retard.
S2(t)=U(t-To)[(t-To)+7]
S2(p)=(exp^-2p/p²)+7(exp^-2p/p)
OK.
Pour la 1, il te suffit de tester les valeurs (il y a une parenthèse ouverte et pas refermée je la néglige) :
S1(t)=2tU(t) + t(U(t)(t+2)=2tU(t)+t(t+2)U(t).
Pour t<0, on a bien S1(t)=0 puisque U(t)=0
Pour t>=0, U(t)=1; donc tu as écrit S1(t)=2t+t(t+2)=t²+4t. Pour t=1 tu trouves 5, pas 2 comme la fonction de l'énoncé.
Alors oui, il faut évidemment utiliser un retard pour que ça change à 2.
Bonne réflexion !
Donc si je modifie on ajoutant le retard:
S1(t)=2tU(t)+(t-2)U(t-2)+4U(t-2)
S1(p)=(2/p²)+(exp^-2p/p²)+4(exp^-2p/p)
Et pour les autres?
Pour t>2, 2tU(t)+(t-2)U(t-2)+4U(t-2)=2t+(t-2)+4 = 3t+2 puisque u(t)=1 et u(t-2)=1
Ne peux-tu essayer de vérifier toi-même que ce que tu écris correspond à l'énoncé ?????
Pour l'autre exercice, tu connais le retard, pourquoi l'appeler To ?
D'autre part, si S2(t)=U(t-To)[(t-To)+7], alors S2(p)=U(p-To)[(p-To)+7]. Mais S2(p) n'est pas la TL de S2(t), c'est la même fonction !!!
Il serait bon d'apprendre à distinguer les lettres S et s (niveau fin d'école maternelle, début de primaire).
Enfin ton résultat final est faux, le retard n'est pas de 2.
Cordialement.
