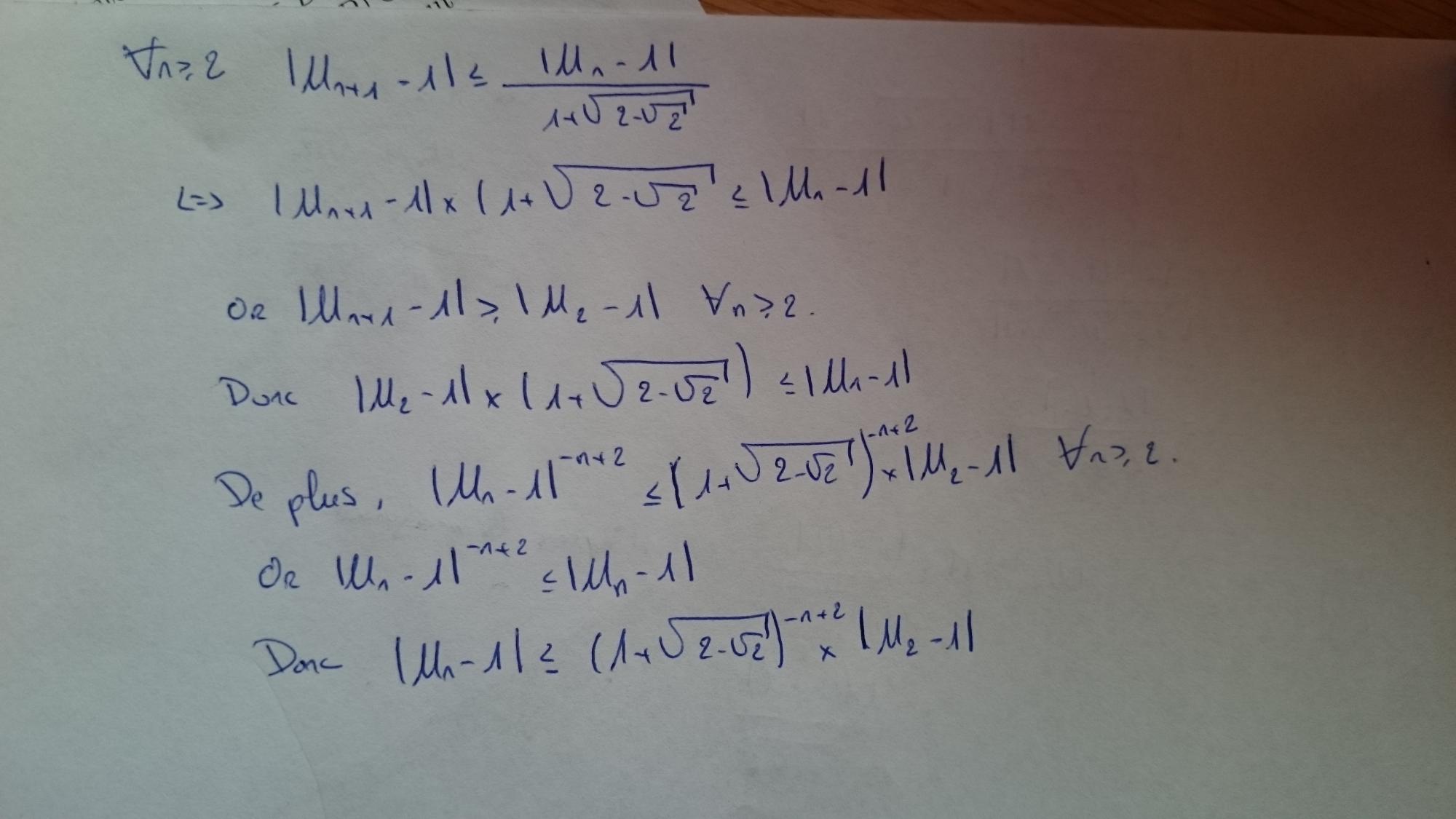Suites

[invite4739a19e]

Bonjour, cela fait un moment que je suis sur cette exercice mais je n'y arrive pas j'ai effectué quelques questions mais j'aurais besoin d'aide s'il vous plait :S
Mon exercice est:
On considère la fonction f définie par f(x) = racine de 2-x pour tout x ∈ D où D = [-2;2].
1) Montrer que la fonction f est continue et strictement décroissante sur D et que f(D)cD. Fait par fonction dérivée et tableau de variation sur [-2 ;2]

Soit c ∈ D , on considère la suite (Un) définie par U0 = c et Un+1= f(Un) pour tout entier naturel n.
2) Montrer que , pour tout n >=2, 0>= Un >= racine de 2. Fait par récurrence
En déduire que pour tout n>=2, |Un+1 -1|<= (|Un -1|)/(1+ (racine de 2 - racine de 2))*.
Conclure que pour tout n>=2, on a |Un -1| <= (1+ (racine de 2 -racine de 2))^-n+2 (|U2 -1|)

*(racine de 2 - racine de 2)) est la racine carré dans la racine carré

3) Que peut -on en déduire pour la convergence de la suite (Un)?
4)Montrer que les suites (U2n) et (U2n+1) pour tout entier n sont adjacentes.

Merci beaucoup. Cordialement.
-----

[gg0]

On ne peut pas t'aider à continuer, on ne sait pas ce que tu as fait !!!

[invite4739a19e]

Vous voulez savoir quoi?

[gg0]

A ton avis, après avoir relu mon message #2 ?

Lis http://forums.futura-sciences.com/ma...ces-forum.html.

[A voir en vidéo sur Futura]

[invite4739a19e]

Ah d'accord excusez-moi, pour la question 1), j'ai étudié la fonction avec un tableau de variation.
J'ai d'abord dit que la fonction était continue en tant que fonction racine carré ainsi j'ai pu la dérivé puis j'ai pu en déduire le tableau sur l'intervalle [-2;2].
D'après le tableau de variation, la fonction f est strictement décroissante sur l'intervalle [-2;2].

Pour la question 2: On avait U0=c avec c appartenant à [-2;2] et Un+1= f(Un).
Donc j'ai fait une récurrence sur n, en posant Pn: "pour tout n>=2, 0<= Un <= racine de 2"
J'ai fait l'initialisation , on trouvait P2 vrai
Puis l'hérédité pour que n+1 soit vrai
Ainsi j'ai pu en conclure que pour tout n>=2, on a 0<= Un <= racine de 2

Et c'est à partir de là que je n'y arrive pas , je ne sait pas d'où il faut que je parte, donnez moi juste une indication s'il vous plait.
Merci.

[gg0]

là, je n'ai rien inventé, tu as dû le trouver seul.
Un petit coup de quantité conjuguée pour faire apparaître , une majoration du dénominateur-quantité conjuguée et c'est fait.

Bon travail !

[invite4739a19e]

Je n'ai pas commencé à utiliser ces mots techniques, c'est le tout début de ma première année en étude supérieure, mais le tout début de ce que vous m'avez dit est logique

[gg0]

Heu .. "quantité conjuguée", c'est une idée classique du secondaire. On peut déjà en parler en troisième (autrefois c'était une connaissance à avoir pour aller en seconde) ou seconde. C'est l'utilisation de (a+b)(a-b)=a²-b² pour faire "disparaître" une racine carrée (dans le a et/ou le b de a-b ou a+b).
Ici, donc on multiplie et divise (pour que ce soit égal) par . on obtien une fraction avec un numérateur simple et un dénominateur compliqué.

Une majoration, c'est le remplacement d'une expression (à priori compliquée) par une autre (simple) plus grande. Ce qui donne une inégalité.

A toi de faire ..

[invite4739a19e]

Je suis arrivée à faire cela

[invite4739a19e]

Puis cela à ce que j'ai compris, mais j'ai 1-Un au lieu d'avoir Un-1

[Philou67]

Merci de faire un petit effort pour mettre l'image dans le bon sens
Cordialement.
Philou67 pour la modération.

[invite4739a19e]

Elle était droite sur mon téléphone portable mais pas sur l'ordinateur à ce que je vois . Désolé.

J'ai retourné l'image. Sur le téléphone portable, c'est le visualiseur d'image qui redresse la photo pour la présenter dans le bon sens. Quand tu l'as poste depuis ton ordinateur, pense d'abord à la vérifier et à la mettre dans le bon sens (le visionneur d'aperçu Windows le permet grâce aux boutons de rotation en bas de l'image).
Philou67 pour la modération.

[gg0]

Que ce soit 1-un ou un-1, comme c'est en valeur absolue ...

Pour l'instant, je ne peux pas lire ...

[invite4739a19e]

Merci beaucoup philou67
Et merci à vous ggo pour toute cette patience consacrée pour moi.
La suite est encore plus dure, on passe de Un+1 à Un et il y a une puissance qui sort :/

[invite4739a19e]

Vous avez pu lire? Aidez-moi encore s'il vous plait, je ne m'en sors pas

[invite4739a19e]

Normalement elle est droite, voila ce que j'ai fait, je ne sais pas si c'est juste

[gg0]

Désolé,

je ne comprends pas la troisième ligne de ce dernier document. Ce qui était sur le document précédent est correct, mais pour passer à la dernière formule (fin du 2), une preuve par récurrence serait une bonne idée (initialisation à n=2, l'hérédité est en grande partie faite.).

Cordialement.

[invite4739a19e]

Bonsoir, je ne savais pas comment faire pour sortir ce U2 et ne sachant pas si la suite Un est croissante ou décroissante, j'ai supposé que Un+1>= U2.

[gg0]

Ton travail n'est pas de supposer, mais de prouver ...

[invite4739a19e]

Bah je ne vois vraiment pas comme faire..

[gg0]

Ben ... tu as une propriété à démontrer pour tout n supérieur ou égal à 2. Tu initialise à n=2, puis tu fais l'hérédité. C'est simple, une preuve par récurrence.

[invite4739a19e]

Pour l'inégalité: |Un-1|<= (1+racine 2- racine 2)^-n+2*|U2-1| ??

[gg0]

Oui.

Ce que tu as publié au message #16 est tout sauf une démonstration. les lignes 3 et 4 n'ont aucune preuve. Après "De plus", il y a une inégalité dont on ne sait pas d'où elle sort, puis "Or" suivi d'une propriété que tu n'as jamais justifiée et à la fin, par miracle (*), la formule que tu devais démontrer. Tu pense convaincre qui, avec ces écritures sans raison ?

NB : l'inégalité telle que tu l'as écrite est fausse, il manque une parenthèse pour l'exposant (règles de priorité des opérations)

(*) en fait, pas de miracle, tu as trafiqué les calculs précédents pour qu'ils donnent la conclusion

[invite4739a19e]

Oui vous avez tout à fait raison c'est exactement ce que je fais
Merci j'ai compris mais après je ne peux pas en déduire si elle converge ou pas

[gg0]

Si,

mais comme tu ne suis pas mes conseils, j'arrête là.

[invite4739a19e]

OK, j'ai suivi tout vos conseils ils sont juste trop flou, je tourne en rond.
Pourquoi faire une récurrence sachant qu'il demande d'en conclure, ça n'a aucun sens.
Et mettre deux jours pour une question c'est utile.
Merci quand même bon week-end.