Quelle puissance de 2 dépasse la tangente d'un angle donné?

[geometrodynamics_of_QFT]

Bonjour à tous les fans de maths,

Je suis confronté à un problème dont je ne parviens pas à trouver la solution.

En soi, il est tout simple, je me pose la question suivante :

Pour quelle valeur de ( l'ensemble des entiers naturels, donc y compris 0) a-t-on , avec un réel donné et fixe?

Par exemple, pour , on a , et , donc la réponse est .

La réponse est évidemment où représente la partie entière. Mais quelles sont les autres méthodes existant permettant de résoudre ce problème? Existe-t-il des méthodes géométriques?

Voici trois illustrations :
- la première est une animation montrant l'itération d'une construction géométrique (rotation + homothétie)
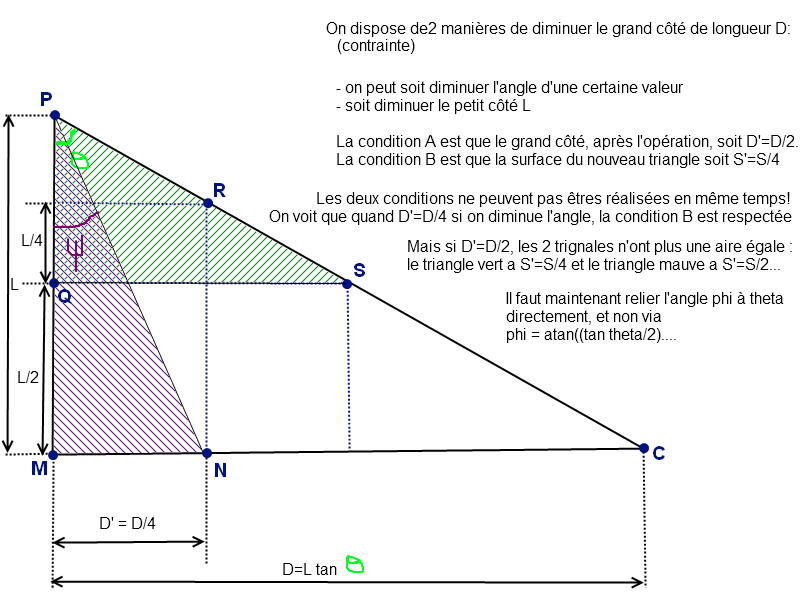
- la seconde montre comment sont définies les grandeurs du problème.
- la seconde tente de schématiser les principales grandeurs et variables du problème récursif en un seul dessin.

anim2.gif
03.png
diminution2.png

La question a pour origine la suivante :

Lorsque , il se produit une singularité, définie dans le sens où les cercles centrés sur la médiatrice d'un segment et passant par les deux extrémités de celui-ci ( et ), voient leur centre s'éloigner à l'infini du segment le long de la courbe sur , mais leurs rayons, eux, ne décroissent qu'à l'allure . Dès lors, pour chaque valeur de , il existe un certain particulier, pour lequel ...J'aimerais pouvoir le déduire dans ce contexte.

Je vous remercie d'avance pour vos conseils et votre aide!
Bien à vous
-----

[geometrodynamics_of_QFT]

PS : sur le 3ème dessin, les points bleus sont les points qui peuvent directement se superposer sur le 2ème dessin, pour n'importe quelle valeur de , moyennant une rotation de et une homothétie de

[geometrodynamics_of_QFT]

mais leurs rayons, eux, ne décroissent qu'à l'allure

Je voulais bien sûr dire :
mais la longueur des segments qui sous-tendent leur arc (càd ), eux, ne décroissent qu'à l'allure


càd à l'allure où les rayons des cercles de construction noirs sur le dessin rapetissent, d'où ma confusion

[geometrodynamics_of_QFT]

J'ai une autre question en lien direct avec ce problème, elle est indiquée dans l'image.
rect.png

On sait que la réponse est , mais j'aimerais le recalculer avec la loi des sinus pour le triangle quelconque ...N'ya-t-il pas un problème "d'unités"?

Sérieux, ce serait plus intéressant si ceux qui ont des remarques les disaient...
Si , sa valeur ridiculeusement petite (voire nulle ici) est affligeante...à quoi sert un forum si ce n'est pour partager et discuter?
Je suis ouvert à toute corrections, remarques, moqueries...je ne mangerai personne...mon but est même plutôt dans un premier temps qu'on m'aide à formuler le problème, plutôt qu'on me donne la solution..Le formuler de manière rigoureuse, dans un formalisme ou plusieurs adéquats, populaires, etc...

entre-temps, j'ai fait aussi cette autre illustration à " constant et n arbitraire" :
thetaconst.png

Elle montre bien que pour un angle fixé, la distance tend vers 0. (on la divise à chaque "pas de 1" de n (n-->n+1)) par 2). Si bien que pour un certain , cette distance devient inférieure à 1.

Et je cherche pour quel cela est réalisé. Des idées?

[A voir en vidéo sur Futura]

[geometrodynamics_of_QFT]

J'ai produit une autre image ci-dessous:


On a un problème lorsqu'on veut égaler deux tranformations visant à réduire une distance en 2 (ici D = L tan 9)

-Si on augmente n de 1 (càd diviser L par 2), en gardant l'angle constant, on arrive à D'=D/2, et le nouveau triangle a une surface S'=S/4
-Si on diminue l'angle jusqu'à phi de telle manière que le triangle formé ait une surface qui est également S'=S/4, on trouve qu'alors D'=D/4.

Cela est dû au fait que dans le premier cas, on diminue le petit côté ET le grand côté, et dans le second cas, on ne diminue QUE le grand côté.

Maintenant, que peut-on faire avec tout ça?
C'est déjà assez dingue pour moi que les 2 triangles hachurés aient la même surface....

[azizovsky]

il faut regardé du côté de la mesure et intégration: Lebesgue,Jordan,Haar....

théorème: tous ensemble infini borné a au moins un point limite .


exemple:.... l'ensemble E est borné, tous ses points appartiennent à un carré avec et
si on le divise en quatre carré, l'un deux est : et on le divise encore..
l'un d'eux à la n ème fois , la différence (ton facteur......)
et

et

point limite de E..............

ps: c'est pourquoi j'aime faire le carrelage....

[geometrodynamics_of_QFT]

il faut regardé du côté de la mesure et intégration: Lebesgue,Jordan,Haar....

théorème: tous ensemble infini borné a au moins un point limite .


exemple:.... l'ensemble E est borné, tous ses points appartiennent à un carré avec et
si on le divise en quatre carré, l'un deux est : et on le divise encore..
l'un d'eux à la n ème fois , la différence (ton facteur......)
et

et

point limite de E..............

ps: c'est pourquoi j'aime faire le carrelage....

Je ne comprends pas du tout...ou alors vaguement des analogies avec mon cas... ça veut dire quoi?
et M, c'est quoi?

Sinon par rapport à mon dernier dessin, est-ce que l'angle est égal à ?
( car )
Que vaut ??

[azizovsky]

d'après le dessin

[azizovsky]

tous ce que je voulais dire, c'est qu'il faut laisser le problème mûrir: regarder dans quel domaine doit être formuler, traiter, ....car les mathématiciens n'ont rien laissé derrière eux (même pas des miettes) sauf pour leurs semblable .