Log(tan θ) : essai N° 1 (Bienvenu à tout le monde!)

[geometrodynamics_of_QFT]

Bonjour à tous,

Voilà déjà une bonne semaine que discrètement, une aventure mathématique se dessine. Partie d'un simple questionnement sur la nature d'un courbe intersectant deux points, celle-ci a révélé un caractère convergent lorsqu'on lui appliquait une homothétie de rapport 1/2 et une rotation d'angle θ de manière itérative.
Nous avons trouvé le point de convergence, et nous nous sommes ensuite demandé à quelle distance du segment se situait le centre du cercle correspondant.
Cependant, une singularité évidente est à l'oeuvre lorsque l'angle θ vaut . En effet, pour cette valeur, le centre du cercle correspondant à chaque segemt est à l'infini, tandis que celui-ci a toujours une longueur finie, donnée simplement par .
Dès lors, comme la variation de est continue, on désire observer le comportement de la distance du centre du cercle associé à un segment dans la "zone de n" telle que cette distance soit proche de l'unité.
Ainsi, si chaque segment a une longueur et une distance au centre avec , on désire déterminer géométriquement pour quel ème segment cela se produit.
L'ayant déterminé, on aura ainsi calculé .

Nous repartons donc ici sur le principe que ces aventures passées sont connues, et dans une certaine mesure elles sont indispensable pour bien comprendre où se situe le problème actuel, lié à l'hyperbole enveloppe.

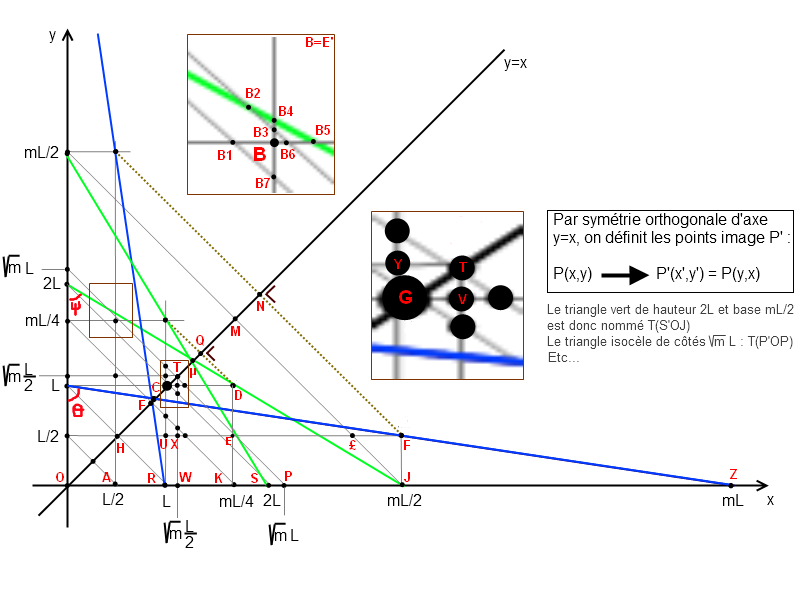
Revoici un dessin "plus propre" que le dernier qui illustre la construction. Celle-ci est disponible en détail sur ce fil.

• Définitions
  • est un réel supposé connu. On peut, si on le désire, lui attribuer la valeur , mais ce n'est pas indispensable dans un premier temps.
  • est le paramètre du système, il représente la tangente de l'angle . toute la construction dépend de lui et bouge avec lui, tandis que L reste fixé.
  • On déduit du point précédent que .
• Question
  ============================== ============================== ============================== ======
  Comment déterminer si connaissant , et ayant comme unique information sur que ?
  ============================== ============================== ============================== ======

A vos claviers!
-----

[geometrodynamics_of_QFT]

Pour ceux qui sont intéressés, j'ai fait une construction Geogebra ici (je débute):
https://tube.geogebra.org/material/simple/id/2859101

Je ne vois plus comment spécifier les foyers de l'hyperbole...mais pas grave.
On voit bien en faisant bouger le point B comment tout bouge avec! c'est excellent

Il doit bien y avoir une possiblité de spécifier des conditions qui garantissent que non?

a+

[geometrodynamics_of_QFT]

Et enfin,

voilà la preuve qu'une détermination géométrique de la transition d'un seuil est possible (pour ceux qui ne parviennent pas à manipuler le projet Geogebra)
Sur les 9 images ci-dessous, on diminue progressivement le paramètre m, pour un L fixé donc.
On voit différentes transitions de second ordre (3 triangles au lieu de 4), mais la principale transition s'opère pour , pour laquelle 2 triangles uniquement "survivent" (vous m'avez compris). En bonus, ce sont 2 paires de triangles d'angle différents qui fusionnent! (et non le bleu avec le bleu, et le vert avec le vert), càd que la relation entre leurs angles que l'on cherche devient triviale! C'est précisément les conditions drastiques ayant lieu à ce moment sur les différentes mesures qui nous permettront de déterminer si l'itération en cours a oui ou non, dépassé la tangente de l'angle , ce qui est l'objectif à atteindre pour déduire ensuite naturellement .
Du bien croustillant à suivre donc


Mais surtout, ô grand surtout, que de ce fil jallissent moult remarques et trolleries diverses, du moment qu'elles titillent certains aspects obscurs, incomplets, problématiques, incorrects, voués à l'échec...qu'elles soient constructives, qu'on ne me laisse pas espérer inutilement quoi...
Venez vous exprimer! J'aimerais me situer, je suis dans la brousse et les gens me suivent du regard silencieusement en ricannant, j'ai l'impression....
Du moins ce n'est qu'une déduction du nombre (nomre de vues-nombre de commentaires)...

N'importe qui peut apporter quelque chose, même vous qui êtes en train de lire! Dites ce que vous en pensez?

Bien à vous

[geometrodynamics_of_QFT]

Dernière petite remarque en passant:

Lorsque , on a , car pour cette valeur de , les 4 triangles ne sont plus que deux, semblables, et et sont alors momentanément complémentaires....

càd que leur relation n'est plus uniquement , mais aussi .........quand je parle de court-circuititer l'atan(tan 9) en passant par l'hyperbole, c'est plutôt à ça que je pense

[A voir en vidéo sur Futura]

[geometrodynamics_of_QFT]

Voilà!

J'ai trouvé une méthode pour exprimer en fonction directement de , et non la tangente de en fonction de celle de .
J'aurais préféré bénéficier de ce forum pour être épaulé dans les calculs, mais étant donné que personne ne veut partager ses connaissances et son expertise, je travaillerai désormais seul, sans rendre compte de mes avancements ici.
Bonne continuation donc à tous les coincés des maths, qui n'ont pas le cran de s'aventurer au-delà des cas d'école et d'exerices dont ils ne connaissent pas la réponse.
signé un contributeur blasé.