Calcul de la meilleure combinaison de resistance en parallèle

[invitece660d78]

Bonjour à tous,
Avec ce titre on dirai que je vais poser une question d’électronique mais je crois bien être à ma place avec la question que je vais vous poser.
Voici le contexte de mon problème : j'ai besoin de faire varier une résistance dans un circuit (pour contrôler un oscillateur). Je dispose de deux résistances variables contrôlées par un PC.
Le nombre de valeurs que peut prendre chaque résistance variable est donc finit; chaque résistance variable peut varier de 40 Ohm à 51040 Ohm par palier de 200 Ohm (donc 255 paliers).
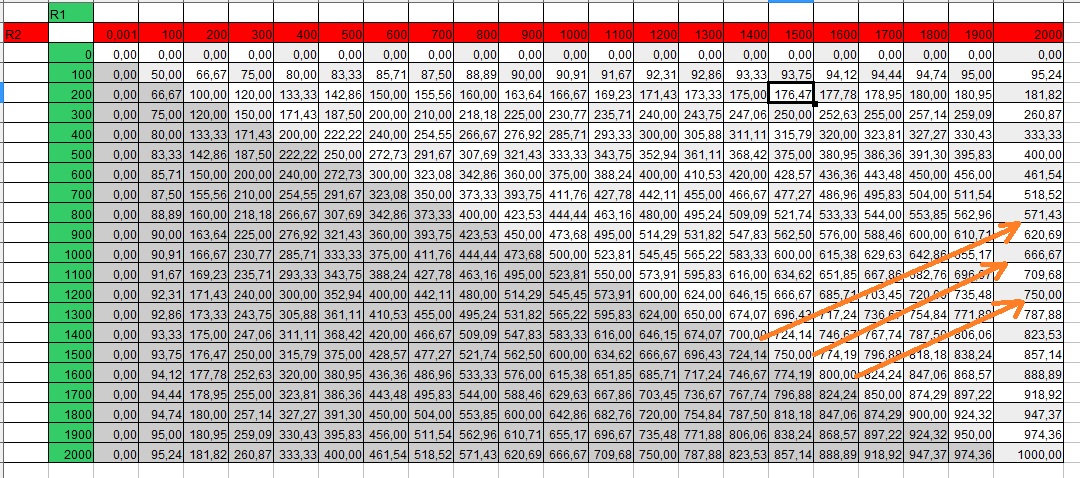
Afin d'augmenter la précision de mon système j'ai pensé à utiliser les deux résistances en parallèle. Ainsi ma résistance équivalente est définie par la fonction
Je souhaite écrire un programme qui me permet de trouver la meilleure combinaison de résistances pour atteindre un résistance souhaitée.
En gros si je vous demande quelle valeur je dois donner à et pour obtenir une résistance équivalente la plus proche de , comment faites vous ?
Je sais bien que la valeur idéale de chaque résistance serai dans le cas ci-dessus de mais ça n'avance pas beaucoup mon problème.

Bien sur je pourrais calculer toutes la valeurs possibles de (65025 possibilités) et comparer celle qui est la plus proche de ce que je cherche.
Je trouverai ça beaucoup plus élégant (et surement plus rapide pour le processeur) de résoudre ça par les mathématiques.
J’espère avoir été assez clair dans ma question,
Merci d'avance,
MichCAN
-----

[plaxtor]

Il faut que tu maximises la fonction (x,y) ---> xy/(x+y) avec comme contraintes min=<x,y<=max.
Si tu calcule ton gradient, alors tu remarques que les deux coordonnées sont toujours positives où nulles. C'est à dire que ta fonction sera croissante pour x ou y croissant. Donc tu peux prendre x=y=max.

Bonne journée

[invitece660d78]

Haa, je me disais bien que j'avais pas assez de neurones pour répondre à la question que j'ai posé...
Je ne comprend pas du tout ta réponse, je n'ai pas franchement les connaissances mathématiques suffisantes.
Est ce que tu sais si je peux trouver un programme de ce type quelque part, je voudrais écrire ça en C si jamais j'arrive à faire ça sur papier dans un premier temps

[plaxtor]

Tu maitrises quand même la notion de dérivée ?
Si tu dérives la fonction que je t'ai indiquée par apport à x, tu te rends compte que la dérivée est positive. Donc c'est une fonction croissante de x. De même c'est une fonction croissante pour y.
Ainsi il faut que tu prennes x et y les plus grands possible (c'est logique, si tu augmente l'une des deux résistances, tu augmentes forcément la résistance totale).

[A voir en vidéo sur Futura]

[Médiat]

Bonsoir,

J'ai peur que la solution de plaxtor ne convienne pas, car il y a des contraintes sur R1 et R2. Personnellement j'écrirais R1 = 40 + 200x, R2=40 + 200 y et l'équation à résoudre en x et y (qui sont des entiers >= 0) devient presque diophantienne (ce qui ne permet pas de trouver simplement, à ma connaissance le meilleur couple (x, y)

[Resartus]

Bonjour,
Ma comprehension du problème posé est que tu veux pouvoir régler le plus précisément possible la résistance totale, en choisissant au mieux les valeurs n1 et n2, mais sans recourir à des tables de correspondance.
Il est plus commode de raisonner en conductances (c'est à dire l'inverse des résistances) La conductance totale va être la somme des deux conductances.
Or, les variations de la conductance à chaque pas seront d'autant plus faibles que les valeurs n seront plus grandes. La précision de l'adaptation sera meilleure en moyenne* quand l'une des résistances aura une valeur élevée

Donc, un compromis qui doit donner des résultats pas trop mauvais est de procéder comme suit :
1) Trouver pour n1 la valeur de résistance qui donnerait, avec la résistance R2 au maximum, une valeur immédiatement supérieure à la résistance R cherchée.
2) Réduire ensuite la valeur de n2 qui approche le plus la résistance R.
Calculs à faire :
Soit R la résistance à approcher
La conductance pour C1 doit être inférieure à 1/R- 1/51040= (51040-R)/R.51040. Donc n1 va être l'entier immédiatement supérieur à [R.51040/(51040-R)-40]/200

Ensuite, connaissant ce n1, on calcule R1 qui vaut 40+n1*200 et on cherche n2 qui sera la valeur entière la plus proche de [R.R1/(R1-R)-40]/200.

*Ce ne sera en général pas l'optimum, mais cela évite de recourir à des tables volumineuses.

[invitece660d78]

Waw,
merci pour vos réponses !
Il me semblait bien que le résultat était assez délicat à trouver.
Un compromis semble en effet une bonne idée. Concernant la table de correspondance j'aurai au moins besoin d'un tableau de 65 025/2 valeurs codé dans des float (4 octets sur arduino UNO), donc c'est pas possible car je dispose que de 32256 octets.
Un truc étonnant que je souhaiterai partager avec vous, j'ai crée un tableau exel à double entrée avec R1 en ligne, R2 en colonne (avec des valeurs "génériques") dans le tableau le résultat de (R1xR2)/(R2+R1).
On observe que si on lit en diagonale de gauche a droite on obtient des valeurs dans l'ordre décroissant, j'imagine que ce n'est pas un hasard
Je sais pas si ca pourrait m'aider dans ma recherche mais sait on jamais...


Encore merci,
je vous tiens au courant de mes avancées

[plaxtor]

Ha ouais j'ai mal lu le problème désolé!