Interpolation 3D

[invitea85d1d54]

Bonjour,

Tout d'abord je m'excuse si c'est le mauvais endroit pour poster ce message, étant donné qu'il y'a également de l'informatique en jeu.

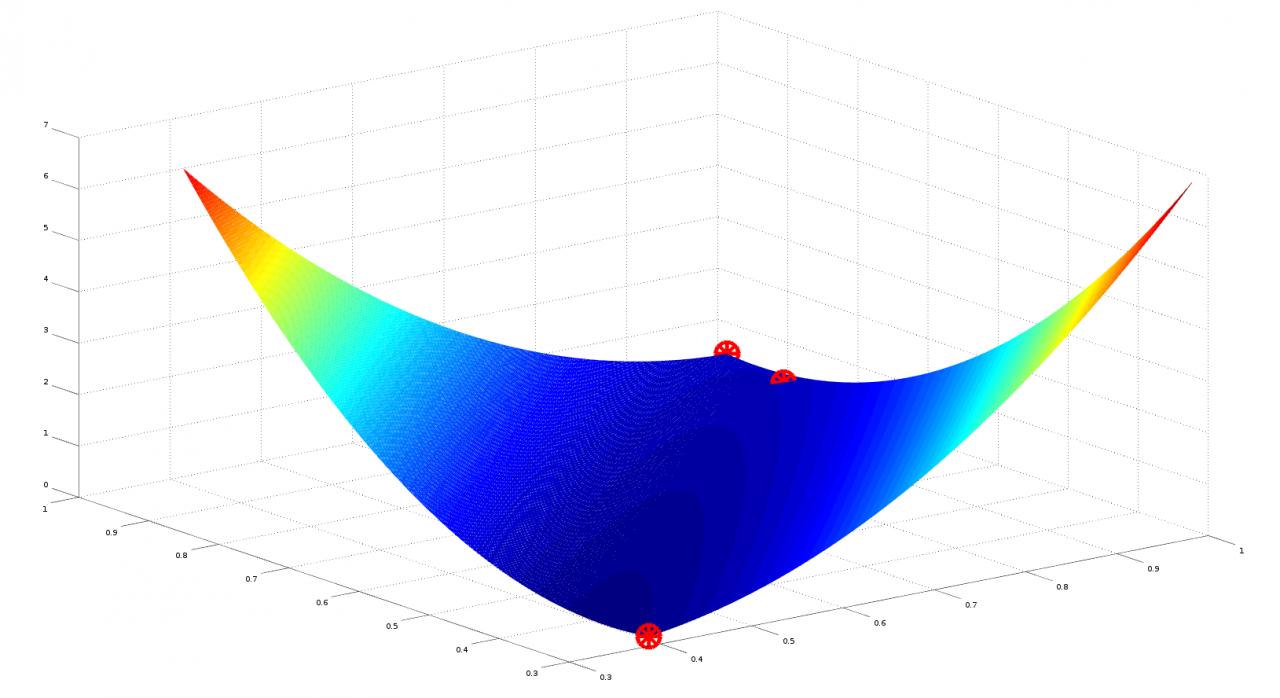
J'ai un nuage de 3 points de coordonnées P1(x1,y1,z1), P2..., P3....
Je souhaiterais à la fois interpoler et extrapoler en fonctions de ces trois points une surface qui à une tendance quadratique (surface bombée), les trois points doivent appartenir à cette surface.

En fait je fait un travail sur excel, malheureusement je ne trouve aucun moyen pour interpoler/extrapoler des points directement dans excel, je ne trouve pas d'application qu'il le permette.

Alors j'ai le choix:
Sois j'entre un algorithme à rallonge sachant que je n'ai pas calculé les "paramètres" qui dépendent des coordonnées (grandeurs physiques) des trois points; j'ai déjà essayé et j'obtiens des surfaces qui partent dans tous les sens, sauf le bon.
Sois il existe un logiciel dans excel qui permet d'inter/extrapoler en 3D; rien trouvé de ce côté là.

Avant que l'on me tape dessus, j'aimerais préciser que: je sais qu'il existe pour une même méthode d'inter/extrapolation une infinité de courbes passant par ces trois points, il me faudrait calculer des "paramètres" dont les coefficients permettent de modéliser une tendance recherchée pour une courbe. Seulement mon niveau de mathématique ne vole pas aussi haut (jamais étudié le calcul matriciel), d'autre part j'essaye de trouver un moyen qui m'évite des faire des calcul à rallonge dans mes feuilles de calculs excel.

Merci, à vous.
-----

[Resartus]

Bonjour,
Comme vous parlez d'abord de surface puis de "courbe", à trouver, je ne suis pas très sûr de comprendre la question. Je vais supposer que c'est bien une surface qu'on cherche

Ce qu'on peut dire, c'est que s'il n'y a que trois points disponibles, et à moins qu'il n'y ait d'autres contraintes à respecter, il y a effectivement des infinités de surface quadratiques possibles.
La plus simple de ces surfaces étant tout simplement le plan (unique, lui) qui passe par ces trois points.

Si vous connaissez par ailleurs des hypothèses complémentaires sur la surface, on peut faire mieux. Par exemple, si vous savez que la surface doit être un paraboloide d'axe 0z et passant par 0,0,0, (qui aura donc la forme ax2+bxy+cy2-z=0), et s'il existe une solution, elle sera unique.

Plus généralement, n'ayant que 3 points, vous ne pouvez résoudre de manière unique qu'un système à 3 inconnues, donc retrouver dans une famille de surfaces paramétrées par 3 variables (a, b, c dans le cas précédent) celle qui passe par les trois points.

[gg0]

Bonjour à tous les répondeurs.

Avant d'essayer de répondre à cette question mal posée, il est utile de lire cette discussion dans un autre forum dans laquelle plusieurs personnes ont essayé d'éclaircir le sujet et des dizaines de messages ont été échangés.
Vue l'explication finalement donnée (surface de réponse d'un dispositif industriel), la question n'a rien à voir avec une interpolation, mais Nonamehero tient absolument à reconstituer une surface complexe à partir de ses trois points. Les maths ne sont pas concernés.
Et il repose sa question comme si personne n'avait donné des pistes.

Cordialement

[invitea85d1d54]

Bonjour,
Comme vous parlez d'abord de surface puis de "courbe", à trouver, je ne suis pas très sûr de comprendre la question. Je vais supposer que c'est bien une surface qu'on cherche

Ce qu'on peut dire, c'est que s'il n'y a que trois points disponibles, et à moins qu'il n'y ait d'autres contraintes à respecter, il y a effectivement des infinités de surface quadratiques possibles.
La plus simple de ces surfaces étant tout simplement le plan (unique, lui) qui passe par ces trois points.

Si vous connaissez par ailleurs des hypothèses complémentaires sur la surface, on peut faire mieux. Par exemple, si vous savez que la surface doit être un paraboloide d'axe 0z et passant par 0,0,0, (qui aura donc la forme ax2+bxy+cy2-z=0), et s'il existe une solution, elle sera unique.

Plus généralement, n'ayant que 3 points, vous ne pouvez résoudre de manière unique qu'un système à 3 inconnues, donc retrouver dans une famille de surfaces paramétrées par 3 variables (a, b, c dans le cas précédent) celle qui passe par les trois points.

Dans mon cas les tables que j'utilise ont ne voit pas le point 0,0,0 car les grandeurs physiques ont un intervalle strictement supérieur. Cependant je pense que cette hypothèse est tout de même intéressante. Une autre hypothèse serait que le points extremum soit l'extremum de la courbe. Je veux en effet obtenir un paraboloïde, seulement inversé la surface bombé est vers le haut.
Donc en partant de cette hypothèse (0,0,0) il me suffira de calculer les paramètres a, b et c,

@ggo: votre message n'a absolument aucun sens, sans vouloir être vexant: je cherche bien un algorithme pour inter/extrapoler, je veux obtenir un algorithme qui est valable quelque soit les valeurs des coordonnée des points, comment cela n'a t-il aucun rapport avec les mathématiques??? Si excel proposerait un outil permettant de faire cela, je ne serais pas allez sur ce forum.

En effet je repose la question pour voir si on peut mieux me guider sur le sujet, car sur les-mathématiques bien que j'ai précisé que je n'ai pas le niveau de math requis, l'un me sort une boucherie de calculs incompréhensible, l'autre me sort une formule hasardeuse je ne sais pas d'où elle sort et attend que je comprennent le tout en un claquement de doigt. Sur un site fan de Excel, on m'a donné une feuille de calcul qui ne correspond pas. Bref, j'ai essayer bon nombre de site sans réellement avoir avancé sur la chose.

D'autre part ggO, ceci est une discussion sérieuse, donc arrêté de la polluer, merci.

[A voir en vidéo sur Futura]

[invitea85d1d54]

Désolé du double poste.

Si quelqu'un se débrouille bien sur Excel et qu'il sait comment je peux interpoler en 3D un nuage définis de points, n'hésitez pas, cela simplifie le problème.

[Dlzlogic]

Bonjour,
J"ai traité énormément de surfaces 3D (2.5D pour être exact).
Au risque de répéter ce qui a déjà été dit, il y a des expressions que vous employez et qui ne sont pas appropriés. Quand on parle de "nuage de points" habituellement, cela sous-entend qu'il y en a beaucoup. Quand on parle de 3 points, cela sous-entend habituellement que ces 3 points définissent un plan, et après on en fait ce qu'on veut.
Par ailleurs, par 3 points on peut faire passer une infinité de surfaces. Une seule sera plane, toutes les autres seront plus ou moins gauches. Elles ont toutes le caractère commun de passer par les 3 points.
Soit vous avez effectivement un nuage de points, c'est à dire un grand nombre, mais vous voulez, hypothèse supplémentaire, que la surface passe exactement par 3 points précis, alors on peut envisager des solutions, soit vous n'avez que trois points et toute solution n'est ni bonne ni fausse.
Enfin, tout programme informatique, Excel entre autres, est fait pour calculer rapidement et sans faute un problème qu'on lui aura appris à calculer, à distinguer de "résoudre". Apparemment, vous ne connaissez pas très bien la signification du terme "algorithme".

[invitea85d1d54]

J'ai déjà dit que je suis au courant qu'il y'a une infinité de surfaces qui passent par 3 points.........Inutile de me le réexpliquer. J'aimerais aller droit au but:

L'équation donnée par Resartus est la même équation qu'un fabricant de gestion moteur utilise pour interpoler (équation quadratique), on garde donc cette équation en tête. Maintenant: comment passer de cette équation là: ax²+bxy+cy²-z=0, à une formule générale (ce que moi j'appelle algorithme de calcul) qui permette de "modéliser" une surface dont les valeurs sur z sont calculées par cette formule même..... un algorithme quoi (je pense que c'est le bon terme). J'ai déjà essayé et j'ai obtenus une courbe qui ne correspond pas à ce que je veux, mais du moins je me rapprochais du but.
Je répète que je travail sur une table sur excel avec des variables sur x et z connues, d'ici je souhaite trouver les variables sur z (interpolées/extrapolées de manière quadratique).

Avec la formule et 3 coordonnés de points on obtiens donc un système de 3 équation à 3 inconnues, il me reste à trouver a, b et c. Dans un premier temps j'ai considéré c=1 pour simplifier le calcul à la main (je ne maîtrise pas le calcul matriciel) et de toute façon j'aimerais intégrer tout cela directement dans excel. Ensuite je continu comment??

[Dlzlogic]

Bon, si on pose la question sous la forme suivante :
On a une surface définie par l'équation ax²+bxy+cy²-z=0.
Cette surface passe par 3 points connus.
Comment déterminer les coefficients a, b, c ?

Si c'est ça la question, alors il suffit d'écrire les 3 équations, et procéder pas substitution.
Vous le faites à la main et sur papier d'abord, et vous notez bien le résultat trouvé.
Puis vous faites la même chose avec votre tableur préféré et vous comparez les résultats.
Il y a d'autres méthodes de résolution que la substitution, mais c'est tout de même la plus simple à comprendre.
Il n'y a aucune raison de considérer c=1.
Il n'y a pas non plus de calcul matriciel.

[invitea85d1d54]

J'ai trouvé les formules pour trouver les coefficient a, b et c.

Mon algorithme est le suivant: z=a(X-x1)i²+b(X-x1)(Y-y1)+c(Y-y1)²+.... idem avec les points 2 et 3
Question: Est-ce c'est comme cela qu'il faut procéder?

Cordialement

[Dlzlogic]

Bonjour,
Comme dit plus haut, on a 3 équations linéaires à 3 inconnues.
La méthode par substitution consiste à écrire a = ... . A droite du signe '=', il n'y a plus que b et c comme inconnue.
Dans les deux autres équations on remplace a par l'expression trouvée. Il reste 2 équations à 2 inconnues b et c.
Dans l'une d'elle, on écrit b= ... . A droite du signe '=' il n'y a plus que c comme inconnue.
Dans la dernière équation, on remplace b par l'expression trouvée.
Il ne reste plus qu'une équation à une inconnue.
Ce que je viens d'écrire est un algorithme, le résultat final est une formule qu'un tableur quelconque résoudra facilement.

[invitea85d1d54]

Bon j'ai essayé la méthode que j'ai cité plus haut et elle est complètement fausse, quelqu'un peut m'expliquer comment on passe de ax²+bxy+c=z pour trois points à un algorithme d'interpolation 3D??? J'ai calculé les paramètres a b et c pour l'interpolation 2D et 3D et j'obtiens un résultat trop important donc faux.

Cordialement

[Paraboloide_Hyperbolique]

Bonsoir,

Essayez la méthode donnée par Dlzlogic: résoudre le système d'équation généré par vos trois points*. Celle-ci fonctionne parfaitement.

*A savoir:
où: sont vos points.

Voici ce que j'obtiens avec trois points pris aléatoirement dans [0, 1]:

[invitea85d1d54]

Merci pour votre réponse Paraboloïde, cependant je vais répondre à mes propres questions et j'espère que cela va également aider d'autres personnes qui cherchent à savoir comment interpoler des points.
Je vais expliquer cela de la manière la plus simple possible.

Mathématiquement parlant:
Pour interpoler/extrapoler des points définis dans un espace à 3 dimensions il faut tout d'abord partir sur une formule mathématique quel qu’en soit la forme, de manière générale plus il y'a de points connus que l'on souhaite interpoler, mieux on pourra donner une "tendance" à notre surface.

Pour simplifier on va prendre celle-ci que j'ai utiliser dans mon travail sur Excel: ax²+bxy+cy²+dx+ey+f (équation quadratique)

Dans mon cas j'ai 3 points calculés de manière physique (points fixes, qui ne changent pas), que je souhaite interpoler en 3D, ce qui me donne 3 paramètres a, b et c. Maintenant pour donner une forme voulue j'ai encore le choix de paramétrer 3 autres points grâce à la formule que j'ai donné, quand je dis "paramétrer" cela veux dire que vous aller donner des valeurs à ces points pour que la surface interpolée donne une forme qui vous convienne.

En gros on aura ici un système de 6 équations à 6 inconnus, qui est donc résolvable. En gros votre formule devra avoir autant de paramètres (a, b, c, d, .....) que de points qui doivent être interpolés. Si vous avez un nuage de point (donc un très grand nombre de points bien répartis sur la surface à interpoler), il sera inutile de paramétrer "à la louche des points". Dans mon cas j'ai seulement 3 points connus, donc j'ai besoin d'autres points pour avoir une surface interpolée qui convienne.

A partir d'ici les mathématiques s'arrêtent, à moi que vous souhaitez résoudre un système de 6 équations à 6 inconnus voir plus, qui aura plus de chance de vous donner une migraine, que de bons résultats. J'ai déjà essayé avec un système à 3 équations 3 inconnus, c'est déjà pas évident.

Il faudra donc avoir un outil pour résoudre des système d'équation, et dans mon cas heureusement Excel est capable de faire cela.
Je ne vais pas expliquer cela ici, mais je vais vous donner un lien qui vous permet de voir cela:
http://www.excel-downloads.com/forum...lation-3d.html

[Dès que j'ai le temps je ferais une synthèse sur le forum du lien, pour regrouper toutes les informations en un post, je mettrais également une feuille excel pour expliquer au commun des mortels comment interpoler en 3D.]

Je tiens à préciser que tous les crédits vont vers Dranreb du forum excel-downloads. Merci à lui.

Cordialement

[ansset]

bjr,
il est absolument nécessaire que tu précises la nature de la forme que tu souhaites.
tu as juste dit "bombée" vers le haut.
que veut dire vers le haut,? si les points sont dans un plan vertical, ou très incliné.
le "haut" est il donc relatif au plan passant par les points ou pas.?
en supposant que oui.
en supposant aussi une certaine symétrie.
ou se situe le point "haut" : au centre de gravité des trois points, ailleurs.?
quelle "hauteur" ? ( paramètre h variable que l'on peut choisir ? )
ou bien on peut aussi choisir l'angle commun de la courbe aux trois points.
En choisissant l'un ou l'autre ( cela revient au même ) , on peut définir un morceau de sphère qui convient.
( sauf si la hauteur est trop grande, supérieure à la distance de G à un point )

bref, il te faut préciser ton "cahier des charges".

[Paraboloide_Hyperbolique]

Bonsoir,

J'estime que Dlzlogic a répondu à la question initiale dans ses posts #8 et #10 pour le cas d'une "surface bombée". Même pour des cas plus généraux ses messages restent valides, moyennant l'adéquation inévitable entre le nombre d'inconnues et le nombre de données* (que ce soient des points ou des contraintes).

Par ailleurs, je pense que celui-ci a fait preuve d'une grande patience pour comprendre ce que souhaite NoNameHero (et qui n'est toujours pas clair) et lui expliquer clairement comment obtenir les résultats (supposés) souhaités.

*Contrainte incontournable quand on veut faire de l'interpolation.