largeur entre 2 méridiens avec 2 disques inclinés l'un par rapport à l'autre

[fabio123]

Dans le cadre du développement d'un code, je rencontre une difficulté qui m'apparaissait simple au début mais que je n'ai toujours pas résolu.

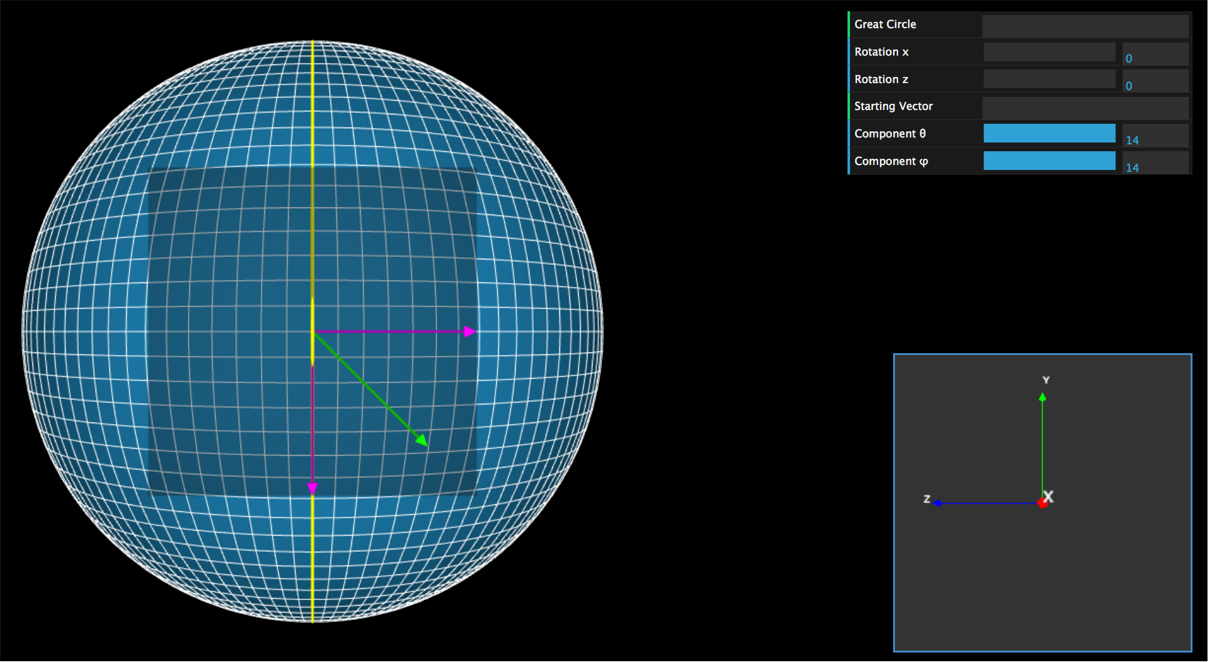
J'ai 2 disques inclinés l'un par rapport d'un angle et qui partagent la même origine et qui ont le même rayon (ils correspondent en fait à la surface de grands cercles sur une sphère). Pour faire simple, considérons le premier disque dans le plan Oxy.

Le périmètre de ce premier disque est parcouru selon l'angle .

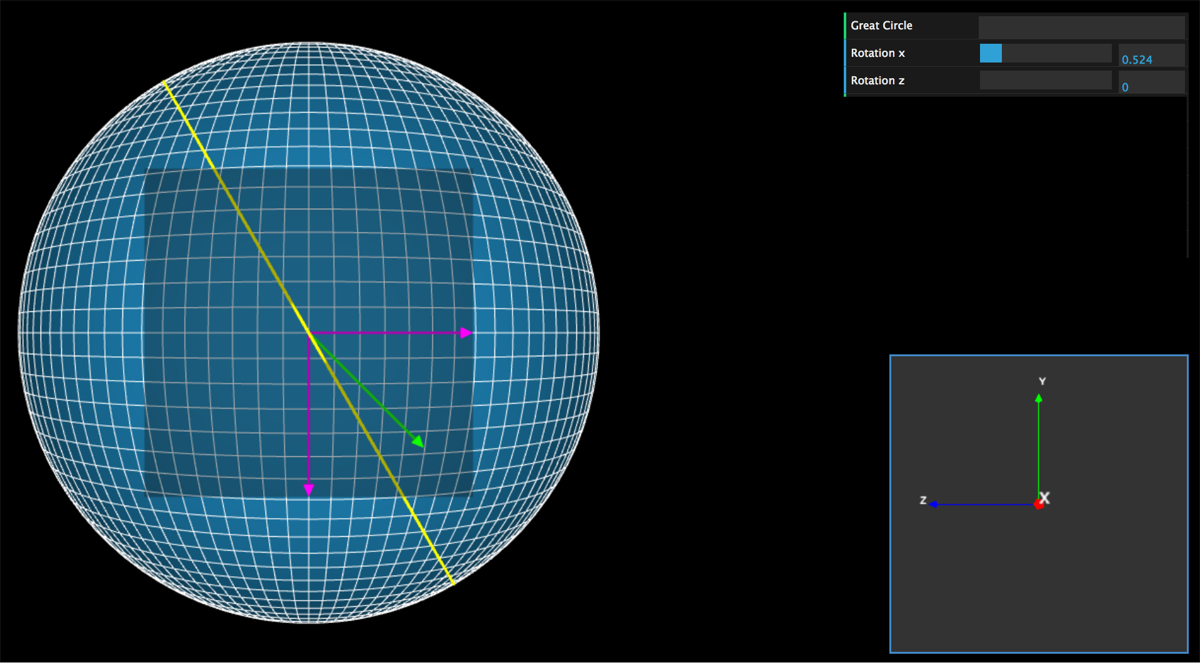
Dans le second disque qui est incliné de selon les axes (Oz) (Oz'), je parcours le périmètre selon l'angle . Je suppose que les angles et ont une origine (je veux dire une valeur égale à 0) géométrique commune.

J'ai besoin d'exprimer la relation entre la variation en fonction de la variation et de la latitude (autrement dit ) du point à partir duquel on fait cette comparaison entre et .

Il me semble aussi que cela peut dépendre de la longitude du point où l'on fait cette relation entre et .

Je pense qu'il y a un lien avec le calcul de la largeur entre 2 méridiens, c'est-à-dire la largeur intersectée entre les 2 méridiens et le premier disque (dans le plan (Oxy)) et l'autre largeur intersecté entre les 2 mêmes méridiens et le second disque incliné d'un angle .

Pour résumer, je cherche une relation qui me permette de faire la correspondance entre la variation d'angle sur le disque incliné et la variation d'angle sur le premier.

Je pensais au début que c'était simplement une relation linéaire avec un facteur mais ça ne donne pas de bons résultats.

Si quelqu'un pouvait me donner des indices ...

Merci par avance
-----

[Dlzlogic]

Bonjour,
Votre explication me parait difficile à comprendre.
Est-ce ce ne serait par tout simplement : "soit 2 points A et B sur une sphère de rayon R, de même latitude L et de différence de longitude alpha. Quelle est la longueur de l'arc AB ?".
Vous parlez de disque de delta etc. J'ai rien compris à tout ça.

[fabio123]

Dlzlogic, vous m'avez amené à utiliser la "distance du grand cercle". J'ai utilisé les 2 premières formules de la page wikipedia suivante.

Pour résumer mon problème, j'ai 1 grand cercle incliné d'un angle par rapport au plan équatorial Oxz (le vecteur e_x est en face de l'observateur).

Je voudrais calculer la correspondance entre une variation le long du périmètre du grand cercle incliné et la variation associée le long du périmètre du plan équatorial Oxz.

J'utilise les formules issues du lien wikipedia pour calculer la différence de longitude sur le plan équatorial en fonctions de la différence de latitude (. Je connais et ainsi que la distance, j'en déduis donc la différence de longitude .

Je rencontre un problème une fois que je me rapproche de la valeur . J'obtiens dans le grand cercle du plan équatorial une valeur associée à cette intervalle égale à .

Si j'ai bien compris, il n'y a pas de bijection sur les 2 , celui du plan incliné et celui du grand cercle équatorial ?

Comment faire le lien entre les 2 valeurs s'il y a bijection ?

Enfin, est-ce que les formules (les 2 premières du lien wikipedia ci-dessus) sont valables pour une différence de latitude ?

Comment modifier ces 2 formules si c'est le cas ? parce que dans mon cas, arrive à une valeur de avant que
n'y arrive.

Merci pour votre aide.

[Dlzlogic]

Bonjour,
Si vous expliquiez votre problème de façon plus précise, et sans termes mathématiques soigneusement choisis, je comprendrai mieux.
D'abord, s'agit-il de la terre ou d'une sphère la représentant ou d'une chose complètement différente ?
Vous parlez de "variation" de "bijection" etc. il y aurait donc une fonction, quelle est-elle ?
Si votre variation approche de pi, alors ce n'est plus un variation. On entend par variation une valeur très petite. Souhaitez-vous refaire les démonstrations de la théorie des projections ? Si c'est ça, j'ai un cours.

[A voir en vidéo sur Futura]

[PrRou_]

Bonjour

Précisons que la variation d'une variable est la différence entre deux de ces valeurs. Cette variation peut valoir Pi , ou tout autre nombre, petit, grand, positif, négatif,...


fabio123
je ne sais pas si j'ai bien compris, mais quand vous dites qu'il n'y a pas de bijection entre les deux delta, je dirais que c'est (peut-être) un problème de discontinuité, pas un problème de bijection.

[fabio123]

Dlzlogic, Voici une image représentant la situation :

image10.png

Le cercle en jaune représente le grand cercle qui est incliné selon l'axe Ox de PI/6 et selon l'axe Oz de Pi/4 (voir les valeurs en haut à droite).

Le plan sombre est le plan tangent au point d'origine des axes de la base locale (e_theta, e_phi) : quand je lance l'animation, je parcours le grand cercle jaune le long de
son périmètre en faisant varier un autre angle (appelons le qui est l'angle local au repère du disque imaginaire (c'est-à-dire le disque qui est le plan du grand cercle jaune et délimité par son périmètre) : à chaque fois je fais varier cet angle, je me déplace le long de ce cercle jaune et l'observateur reste toujours face au plan tangent (c'est-à-dire le carré sombre correspondant à la base locale (e_theta, e_phi).

Je cherche à calculer la variation de l'angle en fonction de la variation de l'angle équatorial de cette sphère (c'est-à-dire la longitude). Le plan local du cercle jaune peut être noté (Ox'y'z') avec z'=0.

En utilisant les 2 premières formules de Great-circle_distance, j'obtiens au début de l'animation (en partant de ) jusqu'à une valeur proche de de bons résultats.

Mais en approchant cette valeur , j'obtiens une valeur pour plus petite, ce qui est normal car comme le plan est incliné par rapport au plan équatorial de la sphère, une valeur donnée correspond à une valeur plus petite pour .

J'obtiens alors une cassure dans l'animation quand j'atteins une valeur . C'est pour cela que je ne sais pas comment gérer et rendre continue cette différence pour les 2 angles pour un angle . Il faut préciser qu'avant le démarrage de l'animation, je pars d'un angle et : mais peut être je fais une erreur sur la valeur de l'angle initial correspondant à l'angle initial local du cercle jaune

Les 2 formules utilisées chacune ont la même cassure que j'ai évoquée ci-dessus, ce n'est donc pas un problème d'erreurs pour les petits angles (qui différencie les 2 formules).

Est-ce que ces 2 formules sont valables quand ?

Merci par avance

[bdom001]

Bonjour Fabio,

je vais me permettre de reformuler votre problème comme je l'ai compris, et d'une manière (autant que possible) qui soit aisément compréhensible par quiconque n'étant pas encore en "immersion"

Tout d'abord le repère orthonormé : (0,x,y,z); On a y (ordonnées) vers le haut, z (cotes) vers la droite, et x (abscisses) sortant du plan et en direction de l'observateur. Cette base ne forme pas un trièdre directe, mais tant qu'on ne fait pas de produit vectoriel, ça ne gène pas.

Les Objets :
- Une sphère (S) de centre 0 de rayon R (à priori, notre bonne veille planète terre);
- Un cercle (C) étant l'intersection entre la sphère et un plan (P), ce dernier étant obtenu par la rotation du plan équatorial d'un angle alpha autour de l'axe (0x)

Le cercle (C) coupe le plan équatorial en 2 points dont M₀ de coordonnées cartésiennes (R,0,0) et de coordonnées géographiques définies de la manière suivante : où et sont respectivement la latitude et la longitude.

Problème : soit un point M du cercle (C) de longitude , quelle est la mesure de l'angle ?

Si c'est bien la question qui est posée, alors voici la démarche que je suivrais :

Si un point M appartient au cercle (C), ses coordonnées satisfont à la fois l'équation du plan (P) et les équations cartésiennes d'un point sur la sphère.

Un point sur la sphère (S) a pour coordonnées

L'équation du plan (P) est

Et là on se rend compte qu'on peut exprimer (latitude du point M) en fonction de (sa longitude) :
z_s est, (selon l'equation d'un point sur la sphère) égal à , qui est (selon l'équation du plan) égal à soit

et donc :

Maintenant, vous pouvez définir n'importe quel point M sur le cercle (C) en fonction de et de sa longitude , et ensuite écrire que le produit scalaire , où est l'angle que vous cherchez

(PS. Je n'ai pas fait les calculs jusqu'au bout)

[bdom001]

J'ai oublié de préciser que ma notation correspond aux de Fabio respectivement

cordialement

[fabio123]

bdom001, merci pour votre aide qui m'apporte des éclaircissements.

Une autre difficulté est que le cercle (C) est initialement incliné selon l'axe (Ox) (de PI/4 sur la figure) mais aussi selon l'axe (Oz) (de PI/6 sur la même figure).

Dans ce cas, je pense que la relation y en fonction de x n'est pas seulement de type ou plutôt "oui elle est vrai" mais dépend aussi de l'angle qui est l'angle initial d'inclinaison du cercle (C) selon l'axe (Oz).

Le point M₀ a donc les coordonnées cartésiennes suivantes : .

Pour un point M quelconque, les coordonnées cartésiennes sont celles que vous m'avez indiquées. Le calcul du produit scalaire est toujours juste (dans le référentiel du cercle (C)) mais par contre, est-ce que l'expression est toujours valable ? ?(c'est-à-dire qu'avec l'inclinaison initiale aussi selon (Oz), devrait aussi dépendre de , je me trompe ??).

Cordialement

[bdom001]

le cercle (C) est initialement incliné selon l'axe (Ox) (de PI/4 sur la figure) mais aussi selon l'axe (Oz) (de PI/6 sur la même figure).

[...] mais dépend aussi de l'angle qui est l'angle initial d'inclinaison du cercle (C) selon l'axe (Oz).

Si votre plan (on laisse tomber le cercle pour l'instant, on sait qu'il est l'intersection d'un plan et de la sphère et d'autre part on cherche l'équation d'un plan) est défini par les deux rotations successives du plan équatorial puis , il est clair que l'angle final entre le plan équatorial et le plan ainsi obtenu n'est ni ni ; mais avez vous réellement besoin l'angle ?

En tout état de cause, l'équation du plan en fonction de et devient :

À des fins simplificatrices, posons ; ; .

L'équation du plan s'écrit alors : .

En affectant au triplet (x,y,z) les coordonnées d'un point
on obtient :
Après une division à droite et à gauche par et quelques calculs de routine, on a finalement


À noter: les conventions pour les angles et
J'utilise la règle du "tire-bouchon" de la main gauche pour définir l'orientation des angles , donc attention aux signes

Pour memo, la règle du tire-bouchon consiste à tendre le pouce d'une de ses mains, d'orienter le pouce dans la direction de l'axe de rotation en le faisant pointer dans le sens des valeurs d'abcsisses croissantes de l'axe, les autres doigts (en les assimilant à des flèches) indiquent alors le sens de rotation des angles croissants.

Partie annexe (pour contrer la possibilité d'une erreur de calcul de ma part): vous pouvez vous renseignez sur la manière de déterminer l'équation d'un plan, sinon vous n'aurez qu'à me demander.

Cordialement

[bdom001]

Je n'ai pas de nouvelles et j'espère que vous vous en sortez. Si je me manifeste à nouveau spontanément, c'est qu'en relisant votre commentaire précédent,

Le point M₀ a donc les coordonnées cartésiennes suivantes : .

votre calcul de M_o ne correspond pas aux calculs que je viens de présenter, et m'inquiète d'autant plus que son ordonnée (sur l'axe (Oy)) est nulle par définition, contrairement à ce que vous écrivez (À moins qu'on ne se soit pas compris sur l'orientation des axes).

En effet M_o se détermine en calculant la longitude du point M du cercle (C) en jaune en posant que sa latitude est nulle, ce qui donne:

soit :


dont on déduit :


Le cercle (C) coupant le cercle équatorial en deux points antipodaux, on prendra par exemple
et donc :

Erratum : dans mon commentaire #10 j'ai oublié le facteur R au moment de récapituler les coordonnées d'un point , mais ce n'est pas gênant pour la suite du calcul puisque le R se factorise avant de disparaître.

Cdlt.

[fabio123]

merci pour votre aide bdom001, je viens de lire votre message et je dois avouer que cela devient un peu confus tout ça pour moi.

1er)

Tout d'abord, comment obtenez-vous l'équation du plan : avec





??

Je retrouve cette équation ci-dessous en prenant la première composante du vecteur obtenu par l'expression suivante (avec




c'est-à-dire l'expression :



Je sais que pour trouver l'équation du plan tangent d'un point sur une sphère centrée en (0,0,0), on a le produit scalaire , c'est-à-dire .

Mais comment faire le lien avec la matrice composée des 2 rotations ( et ).

De plus, il semble y avoir un problème de signe avec la première ligne de la matrice composée; je trouve qu'elle est égale à :



Remarque: dans mon repère, j'ai bien le produit vectoriel


2ème)

sur l'image ci-dessus que j'ai mis dans mes posts précedents, initialement, je peux faire varier avec la souris la latitude du point qui définit le plan tangent de la sphère, c'est-à-dire selon (Oz), je peux faire varier les coodonnées, avant de lancer l'animation, de ce point qui a a lors les composantes suivantes :



Par exemple, sur la capture d'image ci-dessus, on peut voir que :



3ème)

J'ai visiblement un problème dans le choix de la valeur de la longitude au moment de commencer l'animation. Au départ, j'ai la latitude qui est fixée (par , je pourrais donc calculer la longitude initiale correspondante mais je crois que la valeur de cette longitude est celle par rapport au point d'intersection du cercle avec le plan équatorial.

Mais dans ma simulation, je pars d'une valeur nulle pour l'angle dans le repère local du cercle jaune et la simulation consiste à incrémenter cette valeur, qui me sert pour faire tourner la caméra autour de la sphère, le long du périmètre du cercle jaune.

Je ne sais comment gérer, au départ, cette valeur nulle de l'angle dans le référentiel local R' du cercle ( en face de l'utilisateur) et la valeur initiale de la longitude dans le référentiel global R.

[fabio123]

Je dois aussi préciser que la caméra se déplace de la gauche vers la droite de la sphère, c'est-à-dire en décrémentant la valeur dans le repère du cercle jaune : j'ai donc une valeur négative "croissante" au fur et à mesure de l'animation.

Concernant la valeur initiale , je vais tenter de l'appliquer. Merci

[fabio123]

Excusez-moi, dans le produit des 2 matrices de rotation, il y a une erreur :

[bdom001]

merci pour votre aide bdom001, je viens de lire votre message et je dois avouer que cela devient un peu confus tout ça pour moi.

1er)

Tout d'abord, comment obtenez-vous l'équation du plan : avec





??

Tout d'abord, ceci n'est pas l'équation d'un plan, c'est l'équation qui me sert à exprimer la latitude en fonction de la longitude pour n'importe quel point sur le cercle jaune, qui elle même se base sur l'équation du plan qui est la suivante :

Ax+Bx+Cz=0

ensuite, attention à vos expression A, B, C, il y a des coquilles au niveau du formatage, mais vous me faites réaliser que j'avais fait une erreur pour l'expression de C. C n'est pas mais

je vous remets ça :

Je retrouve cette équation ci-dessous en prenant la première composante du vecteur obtenu par l'expression suivante (avec




c'est-à-dire l'expression :

Je trouve l'expression de votre ... bizarre ...

Je sais que pour trouver l'équation du plan tangent d'un point sur une sphère centrée en (0,0,0), on a le produit scalaire , c'est-à-dire .

Mais comment faire le lien avec la matrice composée des 2 rotations ( et ).

Cas simple, qui s'applique bien ici : le plan dont on cherche l'équation passe par l'origine O du repère.
on cherche un vecteur normal au plan de coordonnées puis on écrit que l'équation du plan est
Pour trouver les coordonnées du vecteur normal, il suffit de lui faire faire les rotations en même temps que le plan.

Lorsque le plan ne passe pas par l'origine, il vous faut connaître un point du plan de coordonnées , calculer .
Son équation est alors

De plus, il semble y avoir un problème de signe avec la première ligne de la matrice composée; je trouve qu'elle est égale à :



Remarque: dans mon repère, j'ai bien le produit vectoriel

C'est sûrement parce que vous utilisez la fonction du produit vectoriel de votre environement de developpement, Direct3D (ou peut-être OpenGL) qui reste cohérente avec le repère choisi. En tout cas cela m'informe que lorsqu'on parlera de produit vectoriel je devrai me servir de ma main gauche et non pas de la droite. Cela reste cohérent avec les orientations de et que j'avais choisies.
En revanche, pour la longitude , j'avais pris le sens direct. Il se peut donc que vous ayez besoin de poser

2ème)

sur l'image ci-dessus que j'ai mis dans mes posts précedents, initialement, je peux faire varier avec la souris la latitude du point qui définit le plan tangent de la sphère, c'est-à-dire selon (Oz), je peux faire varier les coodonnées, avant de lancer l'animation, de ce point qui a a lors les composantes suivantes :



Par exemple, sur la capture d'image ci-dessus, on peut voir que :

En fait je vous avais dit au tout début de ma première intervention : « M_o est l'une des intersections en le cercle jaune et le cercle équatorial ». Mais bon, si vous changez en cours de route, c'est pas grave, ça veut juste dire que les résultats que je vous communique ne pourront pas vous satisfaire pleinement. En tout état de cause je vous confirme les coordonnées de M_o, point commun entre le cercle jaune et le plan (xOy).

3ème)

J'ai visiblement un problème dans le choix de la valeur de la longitude au moment de commencer l'animation. Au départ, j'ai la latitude qui est fixée (par , je pourrais donc calculer la longitude initiale correspondante mais je crois que la valeur de cette longitude est celle par rapport au point d'intersection du cercle avec le plan équatorial.

Mais dans ma simulation, je pars d'une valeur nulle pour l'angle dans le repère local du cercle jaune et la simulation consiste à incrémenter cette valeur, qui me sert pour faire tourner la caméra autour de la sphère, le long du périmètre du cercle jaune.

Je ne sais comment gérer, au départ, cette valeur nulle de l'angle dans le référentiel local R' du cercle ( en face de l'utilisateur) et la valeur initiale de la longitude dans le référentiel global R.

Je vous laisse un peu avec ces nouvelles informations

Cdlt

[bdom001]

Fabio,

PS. : Je n'ai pas les mêmes matrices rotations que vous, et à fortiori pas le même produit. À noter que le produit des deux matrices rotations que j'obtiens correspond bien à l'équation du plan que je vous ai proposé (après correction du coefficient C).

[fabio123]

@bdom001, en effet, j'ai pris une mauvaise expression pour la matrice de rotation selon Ox.

Je pense que l'on doit plutôt écrire :



Est-ce que vous trouvez la même matrice finale ?

Pour reprendre vos notations, le vecteur avec le point sur la sphère (S) a pour coordonnées

je peux donc écrire :

avec et

Cas simple, qui s'applique bien ici : le plan dont on cherche l'équation passe par l'origine O du repère.
on cherche un vecteur normal au plan de coordonnées puis on écrit que l'équation du plan est
Pour trouver les coordonnées du vecteur normal, il suffit de lui faire faire les rotations en même temps que le plan.

Si je poursuis, le vecteur défini ci-dessus est le vecteur normal au plan tangent au point (x_s, y_s, z_s).

Je peux alors écrire le produit scalaire :



Mais à partir de cette équation, comment faire intervenir les angles et pour obtenir votre relation suivante :

avec





???

Excusez moi si ça parait évident pour vous.

[bdom001]

@bdom001, en effet, j'ai pris une mauvaise expression pour la matrice de rotation selon Ox.

Je pense que l'on doit plutôt écrire :



Est-ce que vous trouvez la même matrice finale ?

Non, je n'ai pas le même résultat, mais je pense que vous avez juste inversé l'ordre de multiplication des deux matrices.

Je peux alors écrire le produit scalaire :

Si un produit scalaire est nul, il ne peut pas être égal à !!!

Mais à partir de cette équation, comment faire intervenir les angles et pour obtenir votre relation suivante :

avec





???

Excusez moi si ça parait évident pour vous.

A,B,C sont les coordonnées d'un vecteur normal au plan : Je pars du plan équatorial (dont un vecteur normal est (0,1,0)), et je lui fait subir les deux rotations successives R(Ox) et R(Oz) dans l'ordre. Il s'agit juste d'un "petit" exercice de visualisation.

Bon, il y a de la confusion. En partie d'ordre mathématique de votre part, mais aussi de compréhension objective de ma part.

Alors on va essayer d'être efficace en se penchant uniquement sur le deuxième problème. Et pour cela on va oublier un peu la partie mathématique "technique" et oublier le calcul matriciel. Ce dernier est un outil puissant lorsqu'on passe de la théorie à la pratique, mais d'aucune utilité pour expliquer une démarche à suivre.

Donc : remarque à caractère général :
Vous avez sûrement conscience qu'il existe une difficulté pour le demandeur à faire comprendre le problème auquel il est confronté aux personnes qui souhaitent lui apporter de l'aide. Face à ce constat, une "bonne" méthode serait, pour l'aidant, d'expliquer avec ses termes à lui, comment il comprend le problème posé, renversant d'une manière (moindre) le rapport précédent, où c'est au demandeur de faire un effort de compréhension sur la manière dont l'aidant voit les choses, et d'apporter éventuellement les compléments d'informations nécessaires. Ce jeu de ping-pong doit se poursuivre jusqu'à ce que les tenants et les aboutissants soient parfaitement et clairement établi de part et d'autres.

C'est aussi pour ça que j'avais dés le départ naturellement changé votre notation des angles , (par rapport auxquelles je me sentais d'humeur critique), en et respectivement.

En conséquence, voilà où moi j'en suis après notre discussion :
- Pour le repère (O,x,y,z) : on en a déjà pas mal parlé. Je précise que les conventions d'orientation pour les rotations autour des axes (Ox) et (Oz), respectivement et sont conformes avec les vôtres. Pour la rotation autour de (Oy), on verra plus bas.

- Pour la sphère, j'imagine que c'est la surface terrestre. (C'est pratique pour tout un tas de notion commune, comme la latitude et la longitude)

- Le repère géographique ; je ne m'étends pas trop, sauf à préciser que la longitude a pour origine le méridien "de Greewich" passant par le point (R,0,0); le sens croissant étant le même que celui de la rotation terrestre. Autrement dit : main droite placée en O, pouce tendu vers le pôle nord, les autres doigts indiquant alors le sens de rotation des longitudes croissantes; Le fait est que mesure un angle de rotation autour de l'axe (Oy) mais n'est probablement pas conforme avec les valeurs que vous injecteriez dans vos matrice et que je note ; si mes soupçons sont confirmés alors . À vous de me confirmer : En tournant autour de la sphère en suivant l'équateur en augmentant les valeurs d'angles, si vous vous déplacez d'est en ouest ou inversement.

- Le cercle équatorial, intersection du plan équatorial (x0z) avec la sphère. À ce titre, je vous propose d'indicer à 0 tous les points qui se trouveront exclusivement sur ce cercle. Ainsi on rependra donc M_o de coordonnées (R,0,0). Si vous avez besoin d'un autre point, il y aura moyen de lui trouver un autre nom.

- Le cercle jaune, obtenu par les deux rotations puis . Ce cercle coupe le plan (xOy) en un point de coordonnées . Je vous propose d'appeler ce point M₁ et d'indicer avec 1 tous les points qui seront exclusivement sur ce cercle.

Comme ce cercle est obtenu par rotation du cercle équatorial, la rotation entraîne avec elle sa graduation longitudinale , de manière isotrope vers une graduation que j'appelle (que vous aviez initialement appelé ), et qui, tout comme , peut varier de à . Reste maintenant à déterminer l'origine que vous souhaitez pour cette graduation. Le point M₁ ? (pour lequel correspondrait à ); vous me dites.

Finalement, j'ai cru comprendre qu'un objet (point M) se déplaçait sur ce cercle jaune, et que ce déplacement était lié à la connaissance du lien entre (sa longitude, projection méridional sur l'équateur) et (mesure de l'angle ). Toute l'aide que je vous ai apporté jusque là va dans ce sens.

Si il y a des incompatibilités de fond entre votre problème et ce que je viens d'en dire, vous pouvez apporter les corrections nécessaires.

Cordialement

[bdom001]

Bonjour Fabio,
Vous vous en sortez ?

Quand vous me dites « Excusez moi si ça vous paraît évident ». Je ne suis pas sûr de comprendre ce qui vous pose problème :
On cherche l'ensemble des points qui appartiennent à la fois au plan incliné et à la sphère; c'est-à-dire qui appartiennent au cercle jaune.
J'écris simplement que les coordonnées cartésiennes d'un point sur la sphère (x_s, y_s, z_s) satisfont l'équation du plan : A.x+B.x+C.x=0;
c'est-à-dire A.x_s+B.x_s+C.x_s = 0, avec

Vous obtenez alors l'équation :

Le R se factorise (comme je vous l'avais déjà dit) :


Soit :


PS: Par ailleurs je ne comprends pas pourquoi vous voulez faire intervenir le plan tangent à la sphère au point M₁ ou M₀ (sur le cercle jaune)

Cordialement

[bdom001]

[...] les coordonnées cartésiennes d'un point sur la sphère (x_s, y_s, z_s) satisfont l'équation du plan : A.x+B.x+C.x=0;
c'est-à-dire A.x_s+B.x_s+C.x_s = 0

Erratum (coquille) : Il faut bien sûr lire : « A.x+B.y+C.z=0 » et « A.x_s+B.y_s+C.z_s = 0 »

Cdlt

[fabio123]

Bonjour bdom001,

on est d'accord sur la formule de l'équation du cercle jaune qui est de la forme : avec (xs, ys, zs) les coordonnées du point considéré et que l'on peut exprimer sous forme de coordonnées spéhriques ou plutôt avec vos notations

Par contre, je tenais à vous montrer, sur la figure suivante, le cercle jaune que j'obtiens initialement avec :



Vous pouvez voir que le cercle jaune est initialement vertical et perpendiculaire à l'axe (Oz). l'axe pointe vers l'observateur.

D'après cette figure, pour calculer A, B et C, je pense qu'il faut plutôt multiplier le produit (Mat_Rotation_z x Mat_Rotantion_x) par le vecteur et non : Ce produit (de 2 matrices par ce vecteur) permet d'exprimer les coordonnées de dans les coordonnées globales (world coordinates) et il est perpendiculaire au plan Ox'y' du cercle, ceci me donnerait alors (avec la math symbolic toolbox de Matlab) :

% Symbolic variables
syms thetax thetaz
% Rotation matrix along Ox
Rx = [1 0 0; 0 cos(thetax) -sin(thetax); 0 sin(thetax) cos(thetax)];
% Rotation matrix along Oz
Rz = [cos(thetaz) -sin(thetaz) 0; sin(thetaz) cos(thetaz) 0; 0 0 1];
% Vector normal to plane Ox'y'
x=[ 0; 0; 1];
% Transformation for vector normal
y=Rz*Rx*x

y =
sin(thetax)*sin(thetaz)
-cos(thetaz)*sin(thetax)
cos(thetax)

Qu'en pensez-vous ?

Cordialement

[fabio123]

voci une autre capture avec et :

[fabio123]

on est d'accord sur la formule de l'équation du cercle jaune qui est de la forme : avec (xs, ys, zs) les coordonnées du point considéré

Je voulais biensûr écrire :

[bdom001]

Bonjour Fabio,

* Petite précision:

on est d'accord sur la formule de l'équation du cercle jaune qui est de la forme : avec (xs, ys, zs) les coordonnées du point considéré et que l'on peut exprimer sous forme de coordonnées spéhriques ou plutôt avec vos notations

En fait j'écarte complétement la notion de système de coordonnées sphériques (sauf si vous avez une bonne raison de ne pas le faire). Donc si je récapitule, on a bien deux systèmes de coordonnées : un qui est cartésien en 3D (x,y,z) sur lequel je ne reviens pas, et un que je qualifie de géographique en 2D (latitude, longitude) et qui va (c'est comme ça que je l'ai compris) permettre de faire le lien, entre deux points placés respectivement sur deux cercles distincts sur une sphère de rayon R fixe.

S'agissant de la notation, je reprends là les mêmes notations que l'article de Wikipédia que vous aviez cité en référence dans votre commentaire #3.

Alors, maintenant, procédons calmement pas à pas pour parler le même langage, sinon on va s'enliser.

* Premier souci :
Je cite le début de mon premier commentaire (le numéro #7) :

le repère orthonormé : (0,x,y,z); On a y (ordonnées) vers le haut, z (cotes) vers la droite, et x (abscisses) sortant du plan et en direction de l'observateur. Cette base ne forme pas un trièdre directe, mais tant qu'on ne fait pas de produit vectoriel, ça ne gène pas.

et maintenant je crois comprendre avec les informations graphiques et textuelles que vous fournissez, que le vecteur unitaire pointe vers la gauche et non pas vers la droite comme je le croyais. Et effectivement, maintenant la base forme un trièdre direct, et du coup il n'y a plus d'ambiguïté pour le produit vectoriel.

Ces informations sont importantes non seulement pour localiser un point dans l'espace, mais aussi parce qu'elles ont une influence sur le sens de rotation par défaut autour de chacun des 3 axes (pour des valeurs d'angle croissantes, s'entend).
La bonne nouvelle, c'est que cette fois je pense qu'on est raccord sur ce point.

* Deuxième souci:
Vous écrivez dans votre premier commentaire (#1):

J'ai 2 disques inclinés l'un par rapport d'un angle et qui partagent la même origine et qui ont le même rayon (ils correspondent en fait à la surface de grands cercles sur une sphère). Pour faire simple, considérons le premier disque dans le plan Oxy.

puis au commentaire numéro #3:

Pour résumer mon problème, j'ai 1 grand cercle incliné d'un angle par rapport au plan équatorial Oxz (le vecteur e_x est en face de l'observateur).

Et j'avais toujours pris en compte ce dernier cas ("oubliant" le premier).
En tout état de cause, dans tout ce qui vient, je considère que le cercle de référence est bien dans le plan vertical (xOy).

Maintenant :

D'après cette figure, pour calculer A, B et C, je pense qu'il faut plutôt multiplier le produit (Mat_Rotation_z x Mat_Rotantion_x) par le vecteur et non : Ce produit (de 2 matrices par ce vecteur) permet d'exprimer les coordonnées de dans les coordonnées globales (world coordinates) et il est perpendiculaire au plan Ox'y' du cercle, ceci me donnerait alors (avec la math symbolic toolbox de Matlab) :

% Symbolic variables
syms thetax thetaz
% Rotation matrix along Ox
Rx = [1 0 0; 0 cos(thetax) -sin(thetax); 0 sin(thetax) cos(thetax)];
% Rotation matrix along Oz
Rz = [cos(thetaz) -sin(thetaz) 0; sin(thetaz) cos(thetaz) 0; 0 0 1];
% Vector normal to plane Ox'y'
x=[ 0; 0; 1];
% Transformation for vector normal
y=Rz*Rx*x

y =
sin(thetax)*sin(thetaz)
-cos(thetaz)*sin(thetax)
cos(thetax)

Qu'en pensez-vous ?

Que cela me semble correct.
Je ne suis pas particulièrement familiarisé avec l'environnement de Matlab, mais vos matrices et semblent correctes, ainsi que l'ordre de multiplication. Donc votre vecteur normal semble juste aussi.

Je vous laisse poursuivre mais n'hésitez pas à vous manifester si vous bloquez. Notez que je pourrais probablement vous faire tous les calculs, mais il y a, à mon sens encore des ambiguïtés sur la nature du problème que vous cherchez à résoudre, et notamment en ce qui concerne la nature du lien entre la mesure d'un angle sur le cercle de référence (vertical) et la mesure d'un angle sur le cercle jaune. Ce qui fait que le système de coordonnées géographiques que je proposais, pourrait ne pas être totalement pertinent.

Cordialement

[fabio123]

Bonjour,

j'ai repris le calcul fait par bdom001 dans son commentaire #3 mais avec des nouvelles valeurs pour A, B et C (déduites du calcul du vecteur normal ci-dessus). J'ai donc l'équation :



avec :

equations 1*)


J'exprime maintenant (xs, ys, zs) en fonction de la longitude(lambda) et latitude(phi) (en prenant un rayon R=1 pour simplifier) :

equations 2*)



Remarque : je ne suis pas sûr de moi pour le signe - dans l'expression de zs.

Je combine maintenant (equations 1*) et equations 2*) :



que je veux exprimer sous la forme :



J'ai pour cela :



et



J'obtiens donc :



Ensuite, j'ai besoin de définir une longitude de départ égale à 0 pour la simulation. Pour ça, je calcule la longitude correspondante à une latitude nulle, soit :



ce qui donne une longitude

J'aimerais considérer cette valeur comme un offset à retrancher ou ajouter à mon calcul de la longitude quand je me déplace le long du cercle jaune, c'est-à-dire avec l'équation (lambda est la longitude et phi la latitude courante) :



est-ce la bonne méthode ?

[bdom001]

Bonjour,

Remarque : je ne suis pas sûr de moi pour le signe - dans l'expression de zs.

Oui, vos doutes sont fondés. Rappelez-vous mon précédent commentaire, dans le cadre de mon « premier souci », j'avais rétabli la bonne orientation de l'axe (Oz).
On a donc bien :

Finalement, on a :

Je combine maintenant (equations 1*) et equations 2*) :



que je veux exprimer sous la forme :

Oui, mais je vous fais le calcul en corrigeant des erreurs :

Trouver tel que :
l'identité trigonométrique intéressante allant dans ce sens est effectivement :

donc, soit à trouver un angle et un réel tel que : .
soit :


Si un tel angle existe, alors

Calcul de :
En utilisant l'identité : , on a :

soit :


Reste à déterminer , avec :


soit finalement :


donc :


soit finalement :

est-ce la bonne méthode ?

Plutôt
, en tenant compte des corrections.

Sinon, je tenais à dire qu'il m'est difficile de répondre à cette question d'un point de vue global, dans la mesure où je n'ai toujours pas pu établir clairement où vous vouliez en venir. En effet, lors de votre premier commentaire vous vouliez établir un lien entre « et ».
Ce qui me gène, c'est que tous ces calculs sont faits selon la définition classique de la longitude et de la latitude. Lorsque je pensais que votre cercle de référence était sur le plan équatorial, était directement lié à la longitude, donc cela tombait bien.

Maintenant que le cercle de référence est vertical, je ne vois pas comment vous pouvez trouver une relation de type en passant par la longitude telle quelle a été définie. C'est d'ailleurs pour cela que je suggérais précédemment que ce système de coordonnées n'était pas forcément optimal. Par contre vous pourrez avoir : .
, longitude définie comme une graduation angulaire sur le cercle équatorial, donc horizontal (D'un autre côté, si cela s'averait nécessaire, vous pourriez toujours redéfinir mentalement ce système de coordonnées en plaçant le pôle nord en (0,0,R) pour le rendre conforme avec la nouvelle position du cercle de référence (anciennement équatorial), après quoi, les latitudes constantes se trouveraient alors, sur des cercles verticaux parallèles à (xOy) ).

Ensuite, j'ai besoin de définir une longitude de départ égale à 0 pour la simulation. Pour ça, je calcule la longitude correspondante à une latitude nulle, soit :


ce qui donne une longitude

J'aimerais considérer cette valeur comme un offset à retrancher ou ajouter à mon calcul de la longitude quand je me déplace le long du cercle jaune, c'est-à-dire avec l'équation (lambda est la longitude et phi la latitude courante) :

Vous n'avez toujours pas dit ce que c'était que cette simulation. Une caméra qui se déplace ?
Une « longitude de départ » n'est pas précis. Je comprendrais un point de départ, parfaitement défini, et éventuellement un point d'arrivée (au moins une trajectoire orientée, c'est-à-dire avec un sens de déplacement), ça me permettrait de visualiser un peu mieux.
J'aimerais aussi que vous me confirmiez, le cas échéant que vous voulez déterminer une fonction telle que ; avec mesure angulaire en O entre deux points P₀ et P₁ sur le cercle jaune telle que , et , mesure angulaire en O de deux points M₀ et M₁ sur le cercle vertical de centre O dans le plan (xOy) telle que

Vous savez, je passe pas mal de temps sur votre problème par ce que j'essaie de deviner ce que vous voulez, et je doute que qui que soit d'autre ait envie reprendre tout le fil pour comprendre où vous en êtes. Comme je vous l'ai dit, si vous me donnez toutes les infos qui me manquent (description géométrique aussi détaillée que possible, et avec le moins de mathématiques possible), je vous fais les calculs, et ce sera terminé.

Cordialement

[fabio123]

Bonjour bdom001,

je vous ai donné des informations supplémentaires en message privé.

Cordialement.