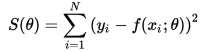fitting ploynômial pour fonction à 2 variables

[invitebb403454]

Bonjour à tous,

Désolé, je vais poser une question qui est peut-être un peu basique, mais j'ai un petit problème pratique, et comme les maths de prépa sont déjà loin, je galère.

Voilà : j'ai un échantillon de points pour une fonction à deux variables, et j'aimerais réaliser un fitting avec, disons, un polynôme de degré quatre en x et trois en y.
Premier réflexe; appeler matlab au secours. Mais suite à un problème de licence dans mon entreprise, je n'aurai pas accès à la l'Optimization Toolbox, ce qui fait que je ne peux pas utiliser les fonctions magiques comme "fit" (qui aurait été idéale)

Du coup, je me suis résigné à coder un truc moi-même. Seulement, j'ai cherché un peu mais je n'arrive pas à trouver de méthode adaptée à ce qu'il me faut... Les courbes de Béziers donne un résultat en paramétrique, dont je ne peux pas contrôler la forme (je n'aurais donc pas mon polynôme f(x,y) comme souhaité). J'ai vu quelques autres trucs du style splines, "moving least squares", etc... Mais ça ressemble plus à des méthodes d'interpolation "esthétiques" pour ainsi dire, qui servent à avoir une jolie surface reliant tous les points sans se soucier d'obtenir une équation d'une forme précise (sauf erreur de ma part).
En désespoir de cause, j'ai essayé, envers et contre tous, de faire une simple méthode des moindres carrés mais ça ne marche évidemment pas du tout (complètement instable, pour des raisons que des gens plus calés que moi en calcul numérique connaissent sans doute ^^)

Du coup, je souhaitais vous demander si vous connaissiez une méthode algorithmique pour ce genre de fitting. C'est tellement simple à faire en monovariable que j'e m'étonne d'avoir à galérer autant en 2D ^^
-----

[invite9dc7b526]

bonjour, qu'appelles-tu "fitting"? Ce n'est pas un terme reconnu en maths (même pas en anglais). Parles-tu d'interpolation ou bien de modèle statistique?

[invitebb403454]

Merci pour ta réponse,

Autant pour moi. Je ne parle pas d'interpolation stricto sensu dans la mesure où je ne souhaite pas imposer à la courbe de passer par tous les points de référence.
Du coup je ne sais pas comment appeler ça si ce n'est "fitting" ou "ajustement"
Il me semble qu'on parle bien d'ajustement par la méthode des moindres carrés, pourtant, non ? En gros j'aimerais avoir l'équivalent de ça, mais transposable à deux variables Je suis clair ?

[invite9dc7b526]

Ok donc tu veux ajuster un modèle polynômial à tes données. La méthode des moindrs carrés est la quasiment même en dimension 1 ou 2 ou k. Si tu ne peux utiliser matlab, fais le avec R (il est gratuit et la syntaxe est proche de celle de matlab).

regarde les fonction lm et poly.

[A voir en vidéo sur Futura]

[invitebb403454]

Ah, c'est vrai, l'idée des moindres carrés tient le coup à 2 variables ?

Ca doit être ma faute alors. J'ai rédigé un petit bout de code sur les moindres carrés (qui marchait très bien à une variable), mais qui donne n'importe quoi en 2 var^^

je joins le code ici :

function a_opti = fitting(x,y,val)

%definition du degre du polynome (le meme en x et y pour l'instant)

degre = 3;

%initialisation du vecteur paramètre comportant n*(n+1)/2 termes

na=degre*(degre+1)/2;
a0= 10*ones(na,1);

%definition du polynome

    function fun = f(a, x, y)
        fun = 0;
        indice = 1;
        for i=1:degre
            lim = degre-i;
            for j=1:lim
                fun = fun + a(indice)*x.^i.*y.^j ;
                indice = indice + 1;
            end
        end
    end

%definition de la fonction à minimiser (moindre carrés)

    function res = residu(a, x, y, val)
        res = sum(sum( (val-f(a,x,y)).^2));
    end

%recherche du minimum avec fminsearch

options = optimset('TolFun',1e-12,'Tolx',1e-12,'MaxIter',100000,'MaxFunEvals',100000);
[a_opti, fval, flag] = fminsearch( @(a) residu(a, x, y, val), a0, options);

%verification des résultats

subplot(1,2,2)
[posq,tempq] = meshgrid(-3:0.25:3);
flag
res = residu(a_opti, x, y, val)
surf( posq , tempq, f(a_opti, posq, tempq) )
subplot(1,2,1)
surf( x, y, val)
end

(Je précise que les x et y arrivent au format "meshgrid" et sont donc des matrices, et pas de simples vecteurs)

[invitebb403454]

Oups ! dans la boucle for qui définit le polynôme, comprendre :

function fun = f(a, x, y)
fun = 0;
indice = 1;
for i=1:degre+1
lim = degre-i+1;
for j=1:lim
fun = fun + a(indice)*x.^i.*y.^j ;
indice = indice + 1;
end
end
end


(j'avais fait une modification malheureuse avant de poster. Mais le résultat est toujours pourri ^^)

[invite9dc7b526]

pourquoi utiliser une méthode de minimisation numérique alors qu'on a une solution explicite? je crois qu'il faut que tu révises tes cours de stats...

[invitebb403454]

Je ne saisis pas... Je croyais que l'idée des moindres carrés était de minimiser le résidu suivant [en 1D ici] :


où les xi sont les abscisses des points de référence, les yi leurs ordonnées et theta le set de paramètres

C'est dans cette optique là que j'utilise une fonction de minimisation. Ca me paraît logique mais je rate peut-être quelque chose ?

[invite9dc7b526]

l'idée des moindres carrés est bien celle que tu penses mais on sait depuis Gauss qu'il y a une solution unique et on sait en écrire l'expression. Dans le cas de plusieurs variables explicatives cette expression implique des calculs matriciels qui en principe sont finis (il n'y a pas besoin de méthode itérative donnant une solution approchée). Regarde la page "régression linéaire multiple" de wikipedia pour les formules. Un modèle polynômial est en fait un modèle linéaire (la linéarité concerne les coefficients). Tu peux programmer la régression avec matlab (il s'agit simplement d'inverser une matrice) mais il y a déjà une foultitude de programmes de régression linéaire qui de plus te donneront des éléments de diagnostic et des représentations graphiques.

[invitebb403454]

Edit :
En fait le programme marche sans problème !
J'ai réussi à avoir accès à l'optimisation toolbox juste le temps d'un test et mon programme donne le même résultat que la fonction built-in de matlab...
C'est juste que le résultat en question est.... assez peu convaincant visuellement.

Pour le test j'utilisais un set de points généré par la la fonction peaks(X,Y), qui génère un ensemble discret de points ressemblant à ça (tracé avec "surf")
peaks.jpg

Et l'ajustement polynomial bicubique donne ceci (pour l'algo officiel et le fait maison) :
fit.jpg

Le R2 me paraît absolument minable (=0.3699), mais c'est vrai que je n'ai que des références à une variable (où on va vite chercher du 0.99), et que ça change peut-être à 2 variables

Le résultat approximé par une surface polynomiale n'a rien à voir avec l'original !! C'est vrai que la surface originale gigote beaucoup, mais quand même... Il n'y a vraiment pas moyen d'obtenir un truc plus propre que cette horreur ?

@minushabens : si vous me dites qu'il existe des solutions exactes, je n'en doute pas. Seulement je ne le savais pas et je faisais avec les moyens à la hauteur de mes connaissances... qui sont a priori suffisants en pratique pour obtenir la résultat que les fonctions officielles de matlab obtiennent. Je vais continuer a priori avec cette fonction de minimisation pour ne pas perdre plus de temps en recherches. Sauf si vous me dîtes que le résultat final médiocre peut être amélioré en utilisant la solution exacte

[invite9dc7b526]

Le résultat approximé par une surface polynomiale n'a rien à voir avec l'original !! C'est vrai que la surface originale gigote beaucoup, mais quand même... Il n'y a vraiment pas moyen d'obtenir un truc plus propre que cette horreur ?

il ne faut pas ajuster une surface polynômiale sans avoir auparavant au moins centré les variables. Tu devrais te renseigner sur les polynômes orthogonaux.

Je vais continuer a priori avec cette fonction de minimisation pour ne pas perdre plus de temps en recherches.

tu cherches à réinventer la roue... ce n'est pas une attitude très professionnelle.