bonjour à tous;
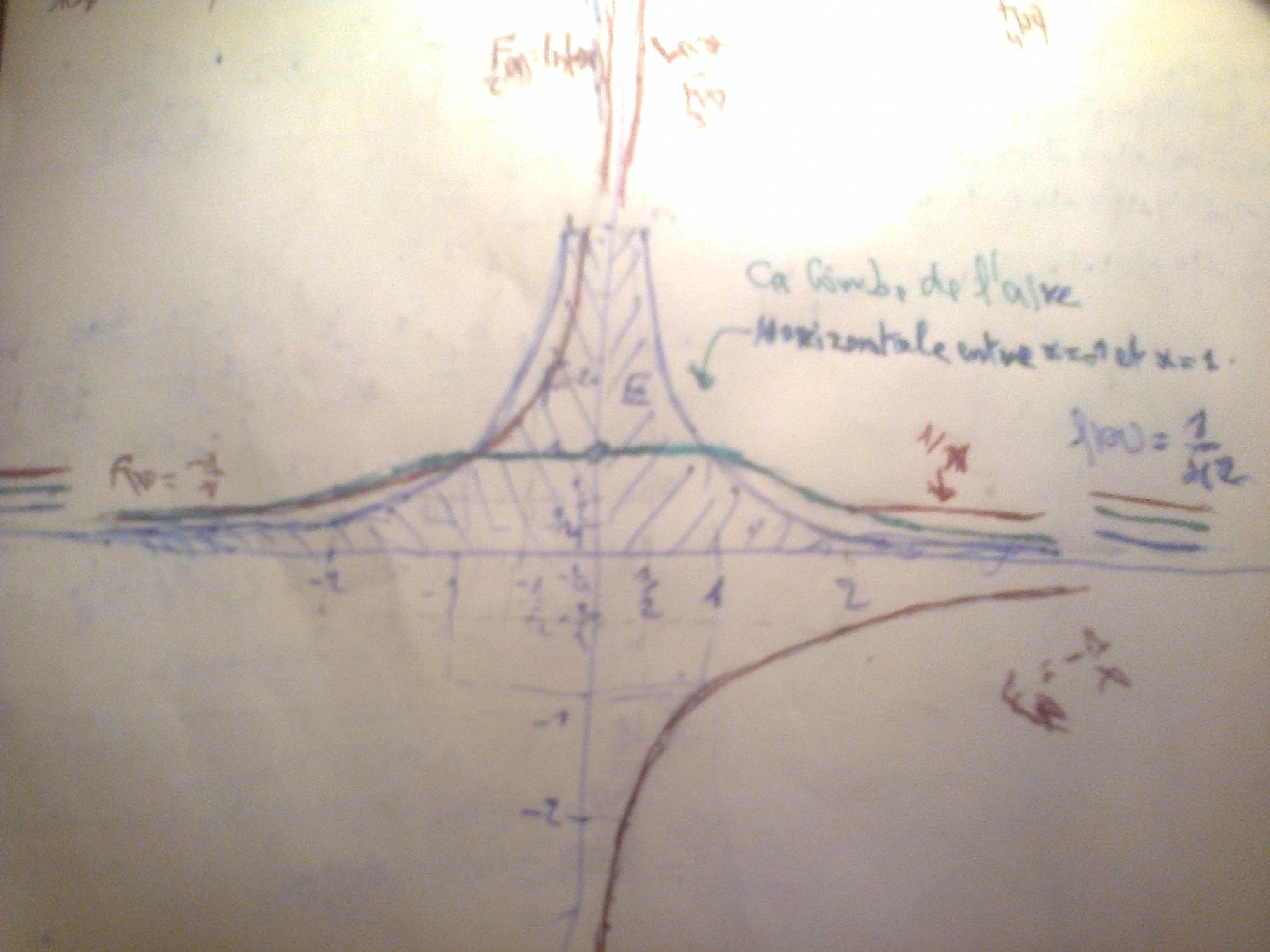
la fonction f(x)=1/x est définie sur R*. si j'appelle F son aire algébrique négatif sur R- (x<0): et E son aire algébrique positif sur R+ (x>0). a quoi ressemble la courbe de ces aires? pouvez-vous s'il vous plait me faire un graphique à main levée sans règle ni mesures précises juste un croquis pour avoir une idée globale sur sa forme et son évolution sur R* ? merci à tous.
Bonjour.
Ta phrase "si j'appelle F son aire algébrique négatif sur R-" ne dit pas quelle aire est considérée. Si c'est l'aire entre la courbe de f et les axes, elle est infinie. Donc parler de "la courbe de ces aires" n'a pas de sens. Je vais supposer que tu veux l'aire entre la courbe de f, l'axe des x et les droites d'équations x=-1 et x=t (pour x<0, t<0) et x=1 et x=t (pour x>0, t>0).
C'est du très classique : La première est la courbe de t--> -ln(-t), la deuxième celle de t--> ln(t).
Tu aurais trouvé ça tout seul si tu avais appris les maths, niveau terminale.
Je ne te ferai pas un graphique, ces courbes sont élémentaires. Et il y a deux courbes, puisqu'il s'agit de questions tout à fait distinctes.
Cordialement.
NB : Vu les absurdités que tu as écrites sur un autre forum, je crains que ma réponse ne te satisfasses pas et que ce fil soit rapidement fermé (Futura ne laisse pas continuer quelqu'un qui raconte n'importe quoi)
[ATTACH=CONFIG]351812bonjour,
bonjour,
est-ce un crime de réfléchir différemment: si oui ca sera de la discrimination envers qui il pense autrement. j'ai le droit de m'exprimer comme tout le monde ici. je suis un adulte , et je viens ici pour l'amour des maths et des sciences. que je deviens un con, une risée un cancre; pas grave, que mon sujet soit répertorier inutile pas grave, tant que j'aurai les mêmes droits que tous. si j'ai tord contre tout le monde cela ne fera pas de mal, mais si j'ai raison, pour l'amour du progrès de la science ca se sera du bien.
j'ai des démonstrations pour corriger une erreur des maths au sujet de la primitive F(x) de la fonction f(x)=1/x.
-1 démonstration:
la famille des fonction fn(x) des fonctions inverses de x définies comme fn(x)= 1/ $x^n$ se divise en deux sous-familles l'une des paires: fn(x)= 1/ $x^2n$ et l'autre des impaires: fn(x)= 1/ $x^2n+1$. étudiant la deuxième:
fn(x)= 1/ $x^2n+1$ ont pour primitive Fn(x)= -1/ 2n $x^2n$ <0.
les primitive Fn(x) sont toujours négatives et impaires. f(-x)=f(x) sur R*.
quand x<0 : la primitive croise la fonction en x / : Fn(x) = Fn(x) <=> (2n+x) $x^2n$ =0 <=> x=-2n (x est différent de 0).
quans n=0 , fo(x) = 1/x . fo(x) est la première fonction de cette sous-famille impaire, donc a aussi une primitive Fo(x) négative et impaire sur R* et ne pas ln(x) : ( ln(x) est ln de la valeur absolue de x, je ne sais pas l'écrire). Fo(x) est donc composée sous forme de 4 fonctions chaque une par intervalle :
quand x<-1: 1/ Fo(x)= - ln(-x).
quand -1<x<0: 2/ Fo(x)= ln(-x) .
les primitives 1 et 2 se joignent en x=-1.
quand 0<x<1: Fo(x)= lnx.
quand 1<x : Fo(x)= - lnx.
les primitives se joignent en x=1.
2 démonstration:
l'aire de f(x)=1/x avec l'axe de x est une aire positive décroissante comme f(x). quand x --> +oo , f(x) -->0 : elle a la droite y=0 comme asymptote horizontale. et la limite de l'aire --> za=0. le zéro aire quand l'aire s'annule. la primitive F(x) s'annule en x=1. x=1 est le maximum de F(x) toujours négative et aussi y=f(x)=1 est le maximum de l'aire algébrique positive E sur l'ensemble R+. comme x=-1 est le maximum de F(x) et y=f(x)=-1 est le minimum de l'aire algébrique négative F sur R-.
avec une suite arithmétique (kn) définie comme telle: kn= n : k1 =1 et r=1. A1 est l'aire de 1/x quand k1=1 <x< k2= 2.
A1 = F(K1) - F(K2) = ln2 - ln1=0,69
A2 quand K2=2 <x< K3=3 :
A2 = F(K2) - F(K3) = ln3 - ln2 = 0,40
A3 = F(K3) - F(K4) = ln4 - ln3 = 0,28
A4 = F(K4) - F(K5) = ln5 - ln4 = 0,22
A5 = F(K5) - F(K6) = ln6 - ln5 = 0,18
Ai = F(Ki) - F(Ki+1) = ln(i+1) - ln(i) quand Ki <x< K(i+1)
A(n-1) = F(K(n-1)) - F(Kn) = ln(n) - ln(n-1) = ln(n/n-1) quand K(n-1) <x< Kn.
en en déduit que l'aire E est décroissant et sa limite tend vers son zéro aire za quand x--> +oo limE = za=0. pareil pour F, sa limite tend vers son za quand x tend vers -oo : limF = za=0.
-3/ démonstration :
alors puisque l'aire E est positive et décroissante sur R*+ (comme sa fonction f(x)=1/x est décroissante) et E tend vers son zéro aire za= lim(aire)=0 quand x tend vers +oo , que représente e=2,718281828 calculé par Euler ?
e^i limite une somme Si de la somme Sn de la suite d'aire réelle A(n-1) telle que Si = ln(i+1) =i quand $e^i-1$ <x< $e^i$. avec une suite géométrique Un= $e^n$ : Uo= 1 et q=e . entre chaque deux valeurs de Un telles que $e^i-1$ et $e^i$ on limite une partie Si=A1 +A2+A3+...+Ai de la somme Sn de la suite d'aire A(n-1) telle que Si=i , i entier naturel il est 1 ou deux ou 3 .... si i=0 x sera entre 1 et e, quand i=1 x sera entre e et $e^2$ etc donc l'aire de 1/x semble constant égale à 1 mais ne représente pas l'aire réelle de 1/x. se sont des sommes toutes égales à 1. e d'Euler nous donne les extremums de l'aire réelle F et E. les droites horizontales y=-1 et l'axe des x limitent l'aire F . les droites horizontales y=1 et l'axe des x limite l'aire E. la courbe en verts sur le graphique donne la courbe des aires F et E avec un trou à l'origine car 0 est éxclut. de 1/x en bleu, et F(x)<0 en rouge .
conclusion: les aires F et E peuvent être représentées par une courbe même si elles sont infinies. la seule différence c'est que le monde entier se trompe sur la primitive de 1/x.
.[/ATTACH]
C'est bien ce que je disais.
"est-ce un crime de réfléchir différemment" Non. Mais de prétendre que la réflexion des autres est fausse parce qu'on ne sait pas ce qu'ils font, oui. Enfin, ce n'est pas un crime, c'est seulement de la prétention et de la bêtise.
Quant à "l'amour des maths et des sciences", la première caractéristique de l'amour, c'est le respect de l'objet de cet amour. Donc tu fais du baratin !
Je ne vais pas rentrer dans le détail de ce que tu écris, d'autres l'ont fait (*), mais tu ne les lis pas et tu prétends parler de maths sans en connaître les règles. Je pense que ce fil mérite d'être fermé.
Ciao !
(*) sur le forum que je citais, par exemple
je suis désolé je ne te cite pas en personne, je parlais en général. puis en maths il n'y a pas de chichi . c'est la raison qui juge. et si on dit a quelqu'un qu'il se trompe se n'est pas une insulte ou manque de respect.
je veux parler de la fonction f(x)=1/ x^2 . sa primitive est f(x)= -1/x. es aire F et E de f(x) sont positives car comme leur fonction. une particularité dans la courbe des aires F et E qu'elle est horizontale à y=1 entre x=-1 et x=1, avec un trou en point M(0,1), car f(x) est définie sur R* et 0 est exclu. le reste de la courbe semble comme pour 1/x : l'horizontale y=0 (l'axe des x) est une asymptote aussi à la courbe des aires F et E. lim(F) = za= 0 quand x--> -oo. lim(E) = za=0 quand x---> +oo. lim(F)=lim(E)= 1 quand x--->0. la courbe est en vert sur le graphique.Pièce jointe 351815
Pièce jointe 351817
désolé erreur du graphique
Salut !
Désolé, j'ai supprimé les pièces jointes, elles étaient illisibles...
Merci de retenter en faisant le point, si tu as utilisé ton téléphone.
Pour la modération
ah non, pas le monde entier. Il y a au moins sirepico123 qui est dans la lumière. Sachons le reconnaître et prosternons-nous.Envoyé par sirepico123
bonjour,
l'étude de la fonction de f(x)=1/x. depuis son tableau de variation a l'analyse graphique de la courbe de 1/x on vois bien que y=0 est une asymptote horizontale. on voit que quand x-->(+,-)oo la lim(f(x))=0. donc la courbe est collée à l'axe des x en (+,-). donc elle ne fait aucune aire avec l'axe des x. l'aire F et E tendent vers leur zéro, que j'appelle le zéro aire. les aires F et E sont décroissant comme leur fonction 1/x.
maintenant le dilemme:
F(x) est bien logarithmique on ai d'accord. la différence de deux valeurs des primitives de x égale à l'aire de la courbe entre ces valeurs de x. mais si F(x)=lnx quand x>1; l'aire devient logarithmique croissant quand x tend vers +. dont il va croître et lim(E)=+oo. qui est contradictoire. pour y remédier il faut utiliser - lnx comme primitive. F(x)= - lnx r'amène l'aire E de rester décroissant et se tendre vers son za à +oo.
pareil pour F(x) quand x<-1. si F(x)=ln(-x) comme dit la théorie en prenant ln de la valeur absolue de x comme primitive de 1/x. donc la limite de l'aire F logarithmique négative va vers -oo. qui est contradictoire puisqu'il va vers le za . pour y remédier il utiliser -ln(-x).
il reste les deux intervalle :
-1<x<0 : F(x)=ln(-x) : et 0<x<1 : F(x)= lnx. au totale F(x) sera composée de 4 fonctions logarithmiques différentes négatives . comme vérification toutes les fonctions inverses impaires de x ; fn(x)= 1/ x^2n+1 ; ont des primitives paires et négatives Fn(x)=-1/ 2n*x^2n. quand n=0 on trouve la première : Fo=1/x. sa primitive Fo est aussi négative et paire sur R*.
c'est faux.
tu peux prendre un a > 0, aussi grand que tu le veux, l'airecar
autre exemple avec 1/x², qui est aussi "collé à l'axe des x". Pour un a > 0, aussi grand que tu le veux tu as :
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
s'il n'y avait que cela de faux
l'avantage avec les maths, c'est qu'il est très facile de le montrer.
ou bien serepico 123 le comprend ( c-a-d qu'il comprend pourquoi ses calculs et formulations sont faux ) et c'est la fin de l'histoire.
ou bien, il ne le comprend pas, en arguant du "penser différemment", ce qui induit qu'il ne comprend pas les maths ( cette partie ) et il n'a plus qu'à retourner à ses cours.
dans ce second cas, c'est aussi la fin de l'histoire.
Cdt
ok merci. si j'ai compris ce que tu veux dire c'est que malgré que la limite de 1/x ou de 1/x^2 ou toute la famille des fonctions inverse de x quand x --> +oo égale à zéro, ces fonctions au voisinage de leurs asymptote y=0 ont une aire très vaste à +oo ??!! et ben si c'est ça je n'arrivais pas a le comprendre. merci beaucoup. j'ai cru que l'aire ne vas pas croître au voisinage de +oo mais décroître pour s'annuler.
pour ton 2ième calcul pour 1/x^2, tu disais un a tellement grand ; alors est ce que 1/a même si il n'est pas égal à 0 , n'est t'il pas tellement petit 1/a=0.00000000...001 = epsilon ou (0+) ?
dernière question s'il te plait, tu as utiliser lnx comme primitive pour 1/x ? si on utilise F(x)= - lnx quand x>1. est ce que la limite avec -lnx quand x tend vers +oo ne deviendrais pas zéro ou (0+) ? parce que je vois que tu viens de démontrer ce que je disait et pas le contraire.
que 0<x<=1 ou que x>1 une primitive de 1/x est tj ln(x) +cte , jamais -ln(x) dont la dérivée vaut -1/x .
oui je le sais merci. le but de ma démonstration est de prouver que cette donnée est erronée. que la primitive de 1/x est toujours NEGATIVE et PAIRE.
BONJOUR,
j'espère que ce graphique de la courbe de 1/ x^2 sera plus net que le précédent.
* la courbe de E de 1/x^2 sur R*+ est confondue avec la courbe de 1/x dans l'intervalle (1,2). (1<= x <= 2), puis elle continue entre les courbes de 1/x et 1/x^2.
* la courbe de F sur R*- est confondue a la courbe de sa primitive -1/x entre -1 et -2, puis continue entre les courbes de -1/x et 1/x^2.
*les courbes de F et de E forment un segment horizontal y=1 muni d'un trou à son centre M(0,1) (car x=0 est exclu) entre x=-1 et x=1.
* quand x<-1 ou x>1 les courbes de F et E 1/x^2 ont la même forme que celles de 1/x sauf dans l'intervalle (-1,0) U (0,1) la courbe de l'aire de 1/x passe par l'origine O(i,j) ( x=0 exclu).
m'enfin, comment peux tu dire une énormité pareille ?
c'est comme si j'affirmais moi, et ce avec force persistance que la fonction e(x) était négative sur R.
de plus elle serait éventuellement paire ou impaire si elle était définie pour x<0 , ce qui n'est pas le cas.
je ne sais pas si on peut parler de "théorie personnelle" pour les maths, mais il s'agit à minima d'une énorme c......e !
ou d'un pétage de plomb, ou de l'abus de substances.
enfin, je pense que ce fil va tourner court, parce que cela suffit.
oubliez ça, du à l'agacement, j'avais lu ln(x) et non primitive de 1/x.
désolé.
Effectivement, l'aire d'une fonction positive (1/x ou 1/x², aire comptée à partir de x = 1 pour fixer les idées) est forcément une fonction croissante. Croissante car on ajoute des quantitiés positives à mesure qu'on calcule l'aire vers des x de plus en plus grands. Le fait que la fonction elle même (1/x ou 1/x²) soit décroissante sur cet intervalle ne change rien à l'affaire : l'aire est une fonction croissante.
Question valeur limite de cette aire, on peut avoir des aires divergentes (valeur infinie) comme avec l'aire de 1/x entre [1,+infini] , et des aires qui tendent vers une limite comme l'aire de 1/x² entre [1,+infini] qui tend vers 1.
Ne pas confondre allure et limite d'une aire et allure et limite de la fonction dont on calcule l'aire.
En ce qui concerne tes messages ultérieurs, c'est à nouveau le même type de confusion. Quand tu écris une énormité comme celle de dire que la primitive de 1/x doit être négative, tu mélanges courbe et pente d'une courbe. Revois ces notions, tu ne les maîtrises pas.
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
Bonjour à tous,
soient f une fonction continue et dérivable dans son Df et E son aire limitée par celle-ci et l'axe des x. on ai tous d'accord sur la propriété suivante: E est engendrée ou créée par sa fonction f. E ne peut jamais agir seule ou à l'opposée de f: (croître, décroître, s'annulée, rester constante...) sans l'intervention de f. E est une conséquence de l'action de f. que f soit positive ou négative si f est croissante, décroissante ou nulle à sa racine xo pour changer de signe, E suit son action: croît, décroît ou s'annule à xo = za pour changer de signe.
la démonstration par absurde est simple: on suppose qu'une donnée est juste, puis on l'utilise. si on abouti à un résultat logique et correcte notre donnée est prise pour juste pour de bon, si non elle est fausse.
on a f(x)=1/x définie sur R*. posons que sa primitive F(x)=lnx sur R*+. Jacknicklaus a démontré que quand x-->+oo , lim(E)=+oo. ce qui veut dire que E croît et diverge vers +oo quand f voisine zéro: quand X-->+oo : lim(fx)=0+ , (asymptote horizontale à y=0). ce résultat n'est ni logique ni juste car il est en contradiction avec la propriété citée plus haut. donc la donnée F(x)=lnx supposée juste se confirme fausse. et refait la même démonstration avec F(x)= -lnx. on aura lim(E) = 1 , quand lim(f(x)=0+. résultat logique et juste. conclusion la donnée supposée juste l'ai vraiment. la primitive de 1/x est -lnx non pas lnx. F est toujours NEGATIVE sur son Df R*.
Bonjour,
Cela part très mal !
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
s'il te plais prenant les exemple faciles : une droite y=ax+b qui s'annule à -b/a ou une parabole ax^2 + bx + c qui a au moins une racine xo. l'aire s'annul aussi à za= -b/a pour la droite et change de signe en passant de l'autre coté de l'axe des x comme sa droite. ou l'aire de la parabole s'annule aussi à la même racine za= xo et change de signe exactement comme sa parabole. l'aire évolue suivant le tableau de variation de sa fonction de la même manière.
malgré la difficulté à comprendre précisément tes alignement de mots.
il y a à la base ( semble t il ) une confusion abrabra.....tesque entre primitive/intégrale et dérivée d'une fonction.
pour ton polynôme ax²+bx+c, c'est sa dérivée qui s'annule en en x0=-b/2a !!!!!!
je comprends mieux d'où te viennent peut être tes autres confusions.
posant une suite arithmétique (Kn) telle que Kn=n : K1 =1 et r=1. l'aire réelle de 1/x est la suite A(n-1) / A1 = ln(2/1) limité quant K1<x<K2 , A2= ln(3/2),
A3 = ln(4/3). A4 = ln(5/4) ....Ai = ln(i+1/i)...A(n-1) = ln(n/n-1). la suite A(n-1) donne les valeurs directes de l'aire de 1/x à chaque intervalle. cette suite est décroissante .
la somme Sn de A(n-1) qui ne donne pas les valeurs de l'aire a chaque intervalle mais des valeurs de Si de Sn. Sn=ln(n). la somme Sn est logarithmique croissante. mais Sn ne représente pas la valeur de l'aire réélle de 1/x. c'est la suite A(n-1) qui le fait. A(n-1) est décroissante.
désolé tu confond la suite A(n-1) et sa somme Sn ; tu utilise des sommes du même aire pour calculer les valeurs de cette aire, et non pas les aires elles même. en plus si on utilise la suite géométrique Un=e^n: Uo =1 et q=e. on fragmente l'aire de 1/x suivant la suite C(n-1) / C1= C2 =c3+...=Ci =...=C(n-1) =1=Si=A1 +A2 = A3 + A4 +A5+A6+A7=...=1 la suite C(n-1) est constante =1. c'est la méthode d'Euler pour trouver e. les termes de C(n-1) sont des sommes Si successives de Sn. en plus le dernier terme C(n-1) c'est le limite de E de ta démonstration en utilisant le b qui a pour lim +oo à +oo: si F(x)= -lnx, quand x--->+oo, lim(E)=lim(ln(a/b)) = 1= C(n-1) quand x=b et x=+oo. tandis que lim(E)=za+=0+ comme lim(1/x)=0+ au voisinage de +oo.
Totalement faux, des a-aprioris qu'un simple dessin contredirait immédiatement (courbe de 2-x, par exemple).soient f une fonction continue et dérivable dans son Df et E son aire limitée par celle-ci et l'axe des x. on ai tous d'accord sur la propriété suivante: E est engendrée ou créée par sa fonction f. E ne peut jamais agir seule ou à l'opposée de f: (croître, décroître, s'annulée, rester constante...) sans l'intervention de f. E est une conséquence de l'action de f. que f soit positive ou négative si f est croissante, décroissante ou nulle à sa racine xo pour changer de signe, E suit son action: croît, décroît ou s'annule à xo = za pour changer de signe.
Mais quand on a une idée fixe, impossible de regarder la réalité !!
parlant d'une façon très simple: assimilons 1/x pour un caillou , et ses aires E sur R*+ et F sur R*- pour ses ombres. F est l'image de E sont isométriques car 1/x est impaire. pour vous au voisinage de +oo et -oo le caillou a une ombre d'une montagne.
Pourquoi ne pas parler maths ?
Ce fil dérive (dans les interventions de Sirepico) vers le grand guignol ! je l'avais prédit !
Bonjour,
On a atteint le fond : on ferme !
Médiat
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
Bonjour,
Tentative de réouverture, ce fil reste cependant sous haute surveillance.
Médiat
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
merci jacknicklaus de ton aide. oui j'avoue que j'ai été dans le flou à tenter le diable lui-même pour avoir une analyse logique sans contradiction. je met les pendules à l'heure. l'aire croît et égale à la somme Sn. dans mes graphiques s'étaient la suite A(n-1) qui décroît (les valeurs de l'aires dans chaque intervalle. finalement j'ai trouvé l'équation de l'aire A de 1/x en fonction de x, A=f(x) sera:
quand x<-1 : A= F(x)= ln(-x).
-1<x<0 : A= -F(x)= -ln(-x).
0<x<1 : A= -F(x)= -lnx.
x>1 : A= F(x)= lnx.
A s'annule en deux za: za1 =-1 et za2= 1 malgré que 1/x ne s'annule jamais. les fonctions inverses de x agissent différemment. en -1 et 1 nous avons deux origines d'aire. et au voisinage de -oo, 0-, 0+ et +oo lim(A)=+oo.
Bon, on y est presque !
Il te reste à bien formaliser l'intervalle sur lequel tu calcules l'aire. Une aire sous la courbe dépend d'une abcisse de départ et d'une abcisse d'arrivée, qu'il faut préciser.
Dire "l'équation de l'aire A de 1/x en fonction de x, A=f(x)", c'est trop vague. Il faut dire par exemple "l'aire A de 1/X entre 1 et x, avec x > 0".
Note aussi qu'on utilise une variable différente pour parler de la courbe (: f(X) = 1/X ) et pour parler de l'aire (: entre 1 et x).
Tu viens en fait de re-découvrir la formule générale de la primitive de 1/x qui est ln(|x|). (log de valeur absolue).
1) pour x <= -1, aire de la courbe entre -1 et x
ou encore, ce qui est la même chose sur un intervalle croissant, de sens opposé, donc changement de signe de l'aire
2) pour -1 <=x < 0
3) pour 0 < x <= 1
ou encore, ce qui est la même chose sur un intervalle croissant, de sens opposé, donc changement de signe de l'aire
4) pour x >= 1
Dernière modification par jacknicklaus ; 20/10/2017 à 16h47.
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
