Bonjour à tous,
Je suis actuellement en train d'étudier la théorie des groupes et j'ai quelques difficultés avec le théorème de factorisation
Soient G, G′ deux groupes et H un sous-groupe distingué de G. Soit f : G → G′ un morphisme de groupes tel que f(H) =eG′. Il existe alors un unique morphisme de groupes g : G/H → G′ tel que le diagramme suivant est commutatif (on pose g = f_barre) :
́Démonstration. — Soit x ∈ G/H. Il existe a ∈ G tel que x = cl(a). Si b ∈ G est un autre représentant de x, alors ab-1 ∈ H et f(a) = f(b).
Si on pose g(x) = f(a), on obtient donc une application lui définie de G/H dans G′.
Soit y=cl(c). Alors g(xy) = g(cl(a)cl(c)) = g(cl(ac)) = f(ac) = f(a)f(c) = g(x)g(y). g est donc un homomorphisme.
Supposons qu’il existe ψ ∈ Hom(G/H,G′) tel que ψ ◦ cl = f ◦ cl. Alors, pour tout x = cl(a), f(x) = ψ ◦ cl(a) = ψ(x). D'où l’unicité.
Questions :
1) Quel est ce i ? Il n'est pas clairement explicité comme s'il coulait de source mais je ne le comprends pas.
2) Dans la démonstration, j'entends bien ab-1 ∈ H. En effet il est question de la relation d'équivalence (xRy ⇔ Hx = Hy ⇔ yx-1∈H). En revanche l'assertion f(a) = f(b) est moins claire. Pourquoi deux éléments de même classe donnerait la même image pour f : G → G′. J'ai vu que l'on peut définir une relation d'équivalence "associée à f" mais ceci n'est pas clairement explicité. Pourquoi ?
3) N'hésitez pas à développer tout point qui vous semble pertinent ou qui permettrait de clarifier les autres démonstrations, notamment celles des théorèmes d'isomorphisme.
Merci beaucoup pour votre aide
-----



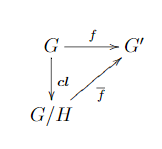
 . C'est tout.
. C'est tout.