probleme primitive

[sciencetape]

f et g deux fonctions dérivables sur ]-1;1 ( dont une est la primitive de l'autre . laquelle ? justifier

-----

[albanxiii]

Bonjour à vous aussi !

Réponse : évident !

[gg0]

Rappel : f est une primitive de g si g est la dérivée de f.

[sciencetape]

comment ca evident ?

[A voir en vidéo sur Futura]

[sciencetape]

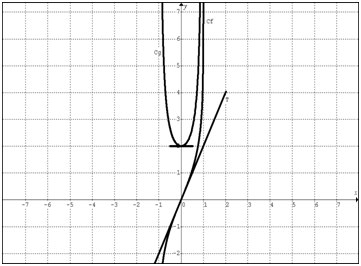
si on pose g la primitive ( la parabole ) son sens de variation est conforme au signe de la fonction f , et pareille si on pose f la primitive , le signe de la parabole est postive et conforme aux variations de f

[Médiat]

Bonjour

f et g deux fonctions dérivables sur ]-1;1 ( dont une est la primitive de l'autre . laquelle ?

Aucune !

[albanxiii]

Aucune !

Vous nous manquez

[ansset]

Aucune !

Pour ne pas semer la confusion chez scientape.
l'énoncé dit textuellement

f et g deux fonctions dérivables sur ]-1;1 ( dont une est la primitive de l'autre . laquelle ? justifier

Il n'existe aucune primitive unique , une phrase correcte aurait été :
...( dont une est une primitive de l'autre ),
ou bien de poser une autre question : laquelle est la dérivée de l'autre.

mais il se peut que ce soit une erreur d'écriture du prof et non de sciencetape

[ansset]

ps: la remarque n'est pas que de forme, mais pourrait induire une erreur de raisonnement de fond.
si f correspond à la parabole et g la fonction qui s'annule en 0 ( pour visualiser )
alors f(x)+C ( constante ) serait aussi une primitive de g(x).

[Médiat]

l'énoncé dit textuellement

Il n'existe aucune primitive unique , une phrase correcte aurait été :
...( dont une est une primitive de l'autre ),
ou bien de poser une autre question : laquelle est la dérivée de l'autre.

C'est bien vous avez compris, mais si sciencetape avait été intrigué par mon intervention au point d'essayer de comprendre par lui-même, cela lui aurait été bien plus profitable.

[minushabens]

En bon français on peut dire de l'une des fonctions qu'elle est la primitive de l'autre, de même que l'une de mes filles peut dire : "je suis la fille de minushabens" nonobstant l'existence de sa soeur.

[ansset]

C'est bien vous avez compris, mais si sciencetape avait été intrigué par mon intervention au point d'essayer de comprendre par lui-même, cela lui aurait été bien plus profitable.

vous avez raison, j'ai d'ailleurs hésité à poster, mais certains ( les nouveaux ) ont parfois tendance à quitter le site en pensant qu'on va les faire tourner en bourrique.
j'ai donc attendu un peu pour voir s'il répondait, ne serait ce que par une interrogation....

ptéte eu tort ?
Cdt

[ansset]

En bon français on peut dire de l'une des fonctions qu'elle est la primitive de l'autre, de même que l'une de mes filles peut dire : "je suis la fille de minushabens" nonobstant l'existence de sa soeur.

mais toi tu es spécial : tu as en fait plusieurs "dérivées" ( tout comme moi )

[Resartus]

Bonjour,
J'ai du mal à comprendre vos réponses.
L'image est petite, mais pour moi, la droite n'est pas une des fonctions cherchées, mais simplement la tangente en zero de l'une des deux courbes,
(qui au passage ne sont pas une parabole et une cubique : on a plutôt l'impression qu'il y a deux asymptotes en -1 et 1)
Et c'est la courbe qui passe par zero, et qui a une pente 2 à l'origine, qui est une primitive de l'autre courbe qui passe par 2 en zero

[Médiat]

Bonjour,

qui est une primitive de l'autre courbe qui passe par 2 en zero

Qui est la primitive

de l'autre courbe qui passe par 2 en zéro (je ne corrige que la syntaxe)

[ansset]

Bonjour,
J'ai du mal à comprendre vos réponses.
L'image est petite, mais pour moi, la droite n'est pas une des fonctions cherchées, mais simplement la tangente en zero de l'une des deux courbes,
(qui au passage ne sont pas une parabole et une cubique : on a plutôt l'impression qu'il y a deux asymptotes en -1 et 1)
Et c'est la courbe qui passe par zero, et qui a une pente 2 à l'origine, qui est une primitive de l'autre courbe qui passe par 2 en zero

tu as raison, j'ai repris aussi moi-même l'appellation parabole innapropriée.
à la vue des courbes je pense que la courbe asymptotique a pour équation
f(x)=1-1/(x^2-1)
on a bien
f(0)=2 ; f'(0)=0 ; f"(0)=2 (*) et elle est asymptotique en -1 et +1, tout comme sa dérivée
(*) d'où la tangente de la dérivée en 0 qui est aussi dessinée sur le schéma.

[ansset]

Donc pour moi ta dernière phrase est fausse.

[ansset]

je corrige, ( désolé Resartus ) on peut aussi trouver un couple ou c'est l'inverse.(*)
comme (4/pi)tan(x*pi/2) ( la fonction strict croissante )
qui s'annule en 0 dont la dérivée vaut bien 2 en ce point.
et qui bien sur ( tout comme sa dérivée présente les bonnes asymptotes )

d'ailleurs si la tangente est figurée , c'est probablement pour induire que la dérivée de la fct strict croissante vaut 2 en x=0.
mais du coup, je ne vois plus comment "prouver" que c'est forcement un cas et pas l'autre.

(*) la fct que j'avais proposée en première intention n'est pas totalement rigoureuse car mes courbes se croisent, mais cela n'induit pas qu'il n'y a pas de solution de ce type.

[ansset]

d'abord désolé de ces posts successifs.
il y a une claire ambiguïté du fait des données du schéma peu lisible. ( à part certaines valeurs qui laissent justement une dualité possible )
il se peut ( s'il est un peu pervers ou malin ) que le prof attende la réponse : les deux solutions sont possibles.
car sans plus d'info, et au niveau lycée, je ne sais conclure autrement.

[Médiat]

Que pensez vous de f(x) = e^x + e^-x et g(x) = e^x - e^-x

[ansset]

bravo, simple et efficace.

mais rien n'interdit une solution potentielle "dans l'autre sens" , si ?
j'en ai fait une approche assez similaire avec une solution de type tan. ( assez proche dans les valeurs )
c'est pourquoi je ne sais conclure sur qui "devrait être une primitive de l'autre".!?
mais peut être avez vous une idée sur le sujet.

[ansset]

correction : tes fonctions ne sont pas asymptotiques en -1 et +1 !
copie à revoir :

[Médiat]

mais rien n'interdit une solution potentielle "dans l'autre sens" , si ?

Je ne vois pas à quoi vous pensez.

c'est pourquoi je ne sais conclure sur qui "devrait être une primitive de l'autre".!?

l'une est la dérivée de l'autre, et vice-versa

[ansset]

l'une est la dérivée de l'autre, et vice-versa

ce qui est demandé, c'est laquelle est la dérivée ( ou une primitive ) de l'autre ( il n'y a pas de vice-versa dans l'énoncé ).
de surcroit les deux fonctions et dérivées présentent des asymptotes en +/- 1 donc votre solution ne correspond pas à l'exercice.