Soufflet pour horloge " coucou "

[sh42]

Bonjour,

J'ai ouvert une horloge " coucou " et à l'intérieur j'ai vu 2 soufflets en papier qui généraient le cri " coucou " si caractéristique. Les soufflets étaient en papier et se pliaient et se dépliaient sans problème, le papier semblant composer des surfaces rigides.

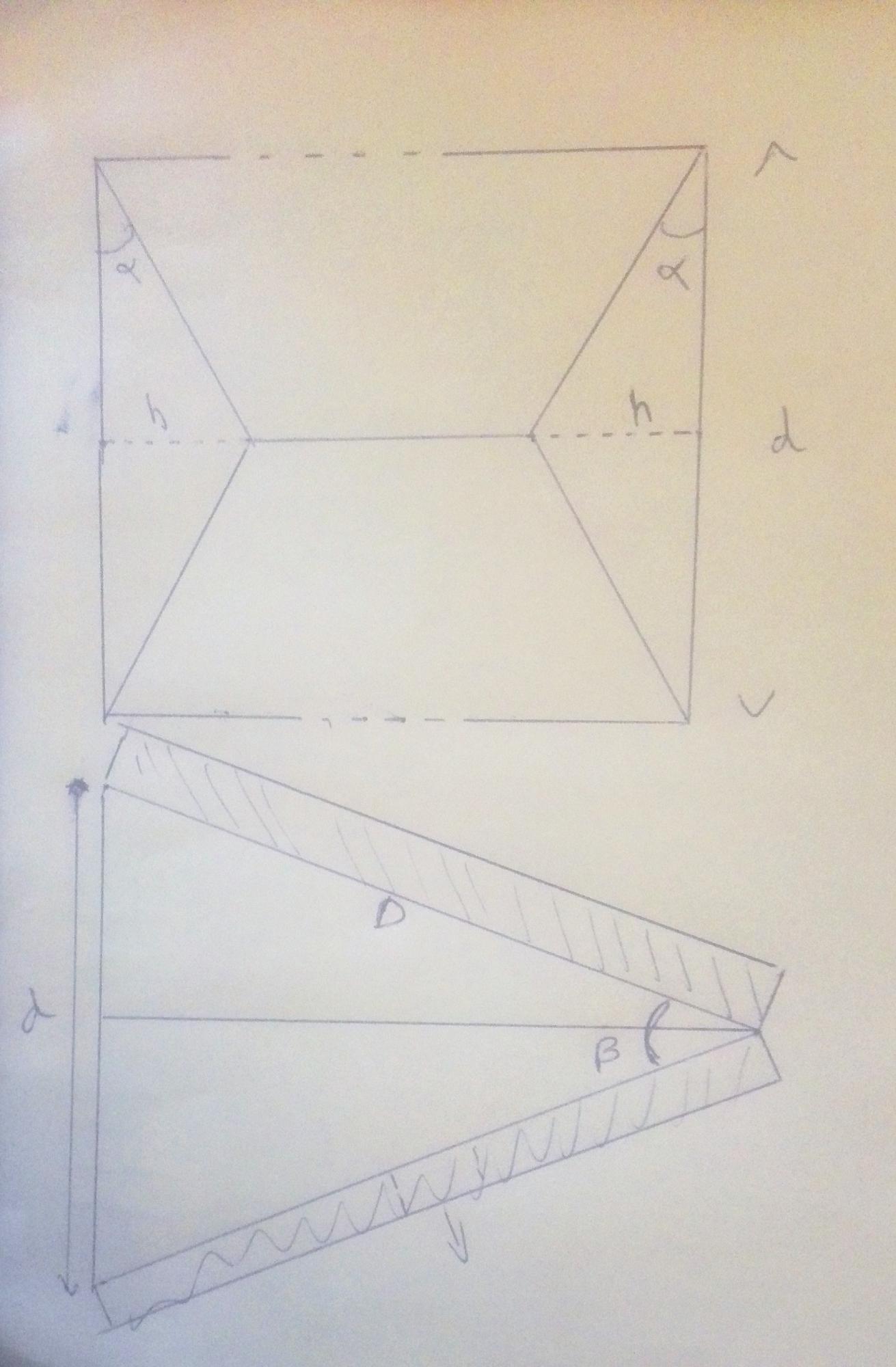
Intéressé, j'ai voulu construire un soufflet plus important. Ayant pris les cotes au pied-à-coulisse, j'ai fait un soufflet plus grand que le vrai, mais au pliage, cela ne s'est plié sans problèmes. Les traits noirs sur la vue de face auraient dû être les lignes de pliage. Or il n'en est rien.

En conséquence, je voudrais connaître, si c'est possible les relations mathématiques qui relient les points A, A1, B, B1, C, C1, D, D1, pour faire en sorte que cela se plie et se déplie sans encombre.
Ces relations mathématiques sont-elles liées à la longueur du soufflet ?
Il y a-t-il une hauteur maximale de dépliage ?


Merci par avance pour toutes vos réponses.
-----

[sh42]

Bonsoir,

Le sujet n'ayant pas l'air d'intéresser les mathématiciens puisqu'il n'y a pas de réponses, ni de questions, je laisse le choix aux modérateurs du forum de transférer vers la technologie ou autre rubriques qui seraient susceptibles d'apporter des réponses.

[SULREN]

Bonjour,

Le sujet n'ayant pas l'air d'intéresser les mathématiciens puisqu'il n'y a pas de réponses, ni de questions, je laisse le choix aux modérateurs du forum de transférer vers la technologie ou autre rubriques qui seraient susceptibles d'apporter des réponses.

Je suis amateur en horlogerie depuis 60 ans. Il m’est arrivé de refaire des soufflets de coucou il y a fort longtemps, mais je ne me souviens pas d'avoir dû faire appel aux mathématiques. C’était du pliage, en respectant bien sûr des relations géométriques, mais cela faisait juste appel au bon sens.

Il y a plein de cas en horlogerie où j’ai dû faire des calculs :
- périodes, réserve de marche,....
- variations de marche en fonction de l’amplitude des oscillations, de la température,
- détermination des profils épicycloïdaux des dents,
- calculs par les fractions continues pour trouver des trains d’engrenages qui réalisent un rapport d’engrenages extrêmement précis (pour la réalisation des complications astronomiques : phases de lune, périodes orbitales, ….)
- etc.

Mais pas pour les soufflets de coucous.

[sh42]

Bonsoir et merci pour la réponse.

en respectant bien sûr des relations géométriques

Ce sont ces relations géométriques qui m'intéressent car la règle de trois avec les erreurs des côtes relevées, cela ne m'a pas donné le résultat escompté.

Et je me dis, qu'avec la puissance de calcul des machines actuelles, la géométrie descriptive est un peu dépassée.

[A voir en vidéo sur Futura]

[SULREN]

Bonjour,
Je ne sais pas s’il est possible de réaliser un soufflet de coucou qu’avec des faces rigides, à arrêtes jointives, articulées par des membranes.
A l’occasion, comme exercice intellectuel j’essaierai d’en analyser la faisabilité par les mathématiques…. assistées de méthodes numériques de résolution .

Ce qui est sûr, c’est que cela n’est jamais envisagé sur les forums d’horlogerie, tant la difficulté serait grande à déterminer ces faces. Si une solution de ce type existait, elle aurait donc été décrite dans les ouvrages d’horlogerie pour la mettre à disposition non seulement des amateurs, mais aussi des horlogers, afin de leur éviter de buter sur "le mur des maths".

Voici le genre de commentaire que vous trouverez sur les forums horlogers :

« Ne te prends pas la tête sur le pliage, il se fait naturellement, tout seul, pendant le montage, regardes plutôt ce tuto : »
https://www.youtube.com/watch?v=H6ArCY9q-nc
« Je m'en suis servi pour refaire mes coucous et c'est le plus simple que j'ai trouvé ».

« Le papier utilisé est: Tyvek 0,14 mm. ou même Ripstop 1/10 mm.
Cela explique aussi très bien: »
https://www.youtube.com/watch?v=a_K6eqiIcX4

On peut remplacer le papier par du cuir spécial pour soufflets, ici par exemple :
http://www.mp-france.com/mfr/parts/coucou-soufflets.htm

Vous trouverez bien sûr des tas d’autres informations sur Internet.

[sh42]

Bonsoir,

Je te remercie pour tes réponses. Les soufflets de coucou que j'ai vu avais des pliures franches qui semblaient se plier naturellement, pas comme celles des sacs plastiques.
Le carton que j'ai plié pour faire les photos, le pliage ne s'est pas fait " naturellement ", bien loin des pliures que l'on fait pour un avion en papier.
Les " jointures " ne ressemblaient pas à celles du soufflet pour cheminée ou de forge pour lesquelles on voit que les pliures se font sur plusieurs millimètres, visibles par les craquelures du cuir.

Je vais regarder les liens que tu as mis, bien que pour youtube, j'ai toujours une appréhension, cela semble tellement facile.

[Resartus]

Bonjour,
Problème amusant : le pliage va en effet dépendre de de la hauteur de la partie arrière en papier (le rectangle qui va se plier en trapèze), mais aussi de la longueur des deux parties rectangulaires en bois du soufflet. Par contre cela ne dépend pas de la largeur de la partie arrière (qui est aussi la largeur des bois)*.

Faute d’outils pour faire de jolis dessins. Je vais essayer d’expliquer en texte.
Appelons D la longueur des deux bois, d la hauteur de la partie arrière et alpha l’angle que font les plis en diagonale avec le rebord (cet angle sera inférieur à 45°).
Alors
1) Les points de pliure se trouvent à h=d/2*tg(alpha) du milieu des bords
2) Une fois plié, le milieu du bord va se déplacer latéralement de a=h(1+cos(2*alpha)) et vers l’intérieur de b=d/2-h*sin(2*alpha).

Ensuite, pour que les deux triangles de chaque coté du soufflet se replient bien, il faudra que la distance entre ce point milieu du bord et l’avant du soufflet (où se rejoignent les deux bois) reste constante quand on plie :
Cette distance vaut L=racine(D²-d²/4) avant pliage et (L-b)²+a² après pliage. Il faut que ces deux valeurs soient égales.
Connaissant D et d, cela donne une équation en alpha, qui est sans doute simplifiable en exprimant les cos(2alpha) et sin(2alpha) en fonction de tg(alpha), ce que je n’ai pas le courage de faire.
Mais si vous avez excel ou un équivalent, le plus pratique est d’écrire ces formules comme fonctions de alpha, et d’utiliser le solver pour trouver la valeur qui rend égales les deux distances…


*du moins, tant que celle ci est supérieure à 2*h

[SULREN]

Bonjour,

-a) Il est vrai que les pliures se font très nettement quand on manoeuvre un soufflet de coucou, pas en se déformant en rouleau par exemple. Ceci laisse supposer que la géométrie de ces facettes a été judicieusement étudiée.
-b) Il est vrai aussi que je n’ai jamais entendu parler de cette géométrie particulière sur les forums d’horlogerie.

Mais les deux affirmations ne sont pas contradictoires.
- Sur ces forums on ne s’intéresse pas trop aux coucous, classés dans l’horlogerie peu reluisante.
- Les questions qui sont posées portent sur la façon de refaire la membrane des soufflets, pas de concevoir des soufflets. En restauration on récupère les pièces en bois de ces soufflets ou on les refait à l’identique.
- C’est de l’horlogerie Forêt Noire, pas française comme les comtoises, les normandes, les mouvements de Paris. Le savoir faire (données géométriques) sur la construction de soufflets qui se plient bien est peut-être restée en Forêt Noire.

Je poserais la question sur le forum Horlogerie Suisse dont je suis membre depuis 2005. Un des membres se souviendra peut-être d’avoir vu quelque chose sur le sujet.

Les équations données par Resartus sont faciles à résoudre en numérique sans avoir à les simplifier. Je ne les ai pas encore comprises, faute de dessin (et peut-être de parenthèses incertaines dans les dénominateurs) mais ce n’est que partie remise.
J’avais dit aussi, dès mon premier post, que cet exercice était intéressant.

[sh42]

Bonjour,

Merci pour vos réponses.

J'ai également du mal à comprendre les équations de Resartus. J'ai essayé de faire le fond du soufflet en prenant la largeur = 2 * h, en pliant, je trouve la pliure d'un fond de sac, bien loin de celle du coucou, où le fond est presque carré.

Les jolis dessins, je m'en moque, je préfère un bon croquis, même avec des lignes courbes car je fais parti de la génération où la géométrie était l'art de raisonner juste sur des figures fausses. Un croquis avec des repères A, B, C,....., une photo et vogue la galère.

Effectivement, le coucou que j'ai eu entre les mains venait de Forêt Noire.

Les coucous, pour de l'horlogerie peu reluisante, je ne partage pas cet avis, car avec les 2 soufflets qu'il faut actionner au bon moment, l'ouverture de la porte, la sortie du coucou, cela fait quelques mouvement en plus que celui du dong des heures et demi-heures.

[Resartus]

Bonjour,
La nuit portant conseil, voici quelques compléments et simplifications :

On peut d'abord remarquer que l'angle alpha de pliage optimal de la partie arrière ne dépend que de l'angle que font les deux bois quand le soufflet est ouvert (appelons-le beta). Cet angle beta est deux fois l'arcsinus de d/2D (où d est la hauteur de la partie arrière ouverte, et D la longueur des bois)

On peut tracer une abaque donnant alpha en fonction de beta. Voici quelques valeurs :

Beta alpha (angles en degré)
5 44,37
10 43,75
15 43,11
20 42,47
25 41,82
30 41,15
35 40,46
40 39,75
45 39,02
50 38,25
55 37,45
60 36,6


Petite question aux experts pour ma compréhension du fonctionnement : comment s'assure t'on que le pliage quand on ferme va bien se faire vers l'intérieur et selon les plis déjà préparés? Le soufflet sans doute déjà un peu fermé en position de repos?

[SULREN]

Bonjour,
J’ai posé la question de la géométrie des soufflets sur un forum horloger.
En attendant de me trouver des informations éventuelles sur le calcul de ces soufflets, l’un d’eux m’a indiqué ce lien sur la façon d’en confectionner.
Ceux-ci ne sont pas destinés à faire « coucou » mais à mettre les glissières des machines-outil à commande numérique à l’abri des copeaux.

http://cncloisirs.com/Construction/P...esGlissi%E8res

Les coucous, pour de l'horlogerie peu reluisante, je ne partage pas cet avis, car avec les 2 soufflets qu'il faut actionner au bon moment, l'ouverture de la porte, la sortie du coucou, cela fait quelques mouvement en plus que celui du dong des heures et demi-heures.

Je comprends la position des horlogers (même si j’aime bien les coucous et que j'en ai deux, y compris avec jeu musical et danseurs):
- Il y a beaucoup de biellettes en fil de fer dans un coucou et de pièces en mouvement, mais toutes actionnées simultanément par une seule came, pas par exemple comme dans un carillon qui sonne les quarts et encore moins comme dans une pendule à sonnerie dite « grande sonnerie ».
- La fabrication des mécanismes de coucou n’a rien à voir avec les techniques de la tradition horlogère. C’est de la tôle emboutie, du fil de fer, etc.
- Le mécanisme chronométrique (ancre, roue d’échappement) est aussi bien moins précis que celui d’une horloge ou pendule de facture horlogère.
- etc.

Mais nous sommes là dans le domaine du goût, du subjectif, avec des discussions qui tournent souvent au dialogue de sourds, pas comme en mathématique.

[Resartus]

Voici un schéma avec les angles et les dimensions que j'ai utilisés dans mes messages.


(Désolé, pas très doué avec mon appareil photo mobile)

[sh42]

Merci pour vos réponses.

@ Resartus, dans le coucou que j'ai vu, la face arrière de pliage n'était pas un rectangle mais un assemblage de 2 trapèzes isocèles identiques, reliés entre-eux par leurs petites bases. Cela se voit bien sur la deuxième photo. De ce fait le pliage ne peut se faire que vers l'intérieure.

[Resartus]

Ah OK, je n'avais pas bien regardé le relief des photos et me suis basé sur le premier exemple video donné par Sulren qui est droit

Le problème mathématique doit être un poil plus complexe (plus de paramètres)…
Je m'y colle...

[SULREN]

Bonjour,
Ces photos montrent la façon qu’a le soufflet de se fermer :

https://www.google.fr/search?q=photo...39UftRunosw5M:

https://www.google.fr/search?q=blase...w=1366&bih=626

[sh42]

@ Resartus, la deuxième solution pour que le soufflet se ferme dans le bon sens est qu'en fonctionnement sa levée soit inférieure à d. Les deux triangles latéraux ne sont pas dans un même plan, donc au pliage, il n'y a pas le choix.

J'ai regardé les vidéos du post 5, dans la première, lorsque les triangles latéraux sont collés, le fabricant appuie légèrement sur le papier de façon à ce que le papier latéral ne soit pas tendu. Dans la deuxième vidéo, le réalisateur mentionne que la base fait 30 mm et la hauteur 31 mm, mais là le tyvek utilisé permet peut-être plus de souplesse que le papier.

[SULREN]

Bonjour,

En ce qui me concerne, je dois reconnaître que je ne suis pas parvenu à trouver un mode de pliage qui ne déformerait aucune des faces pendant l’ouverture du soufflet (ce qui reviendrait à dire que toutes les faces pourraient être rigides, indéformables, simplement articulées entre elles).

J’ai juste trouvé comment modifier légèrement les formes pour réduire la déformation au minimum. Je me doutais un peu de ce résultat, mais il fallait essayer.

On le voit sur l’exemple de soufflet ci-dessous. Je suis navré d’être mauvais en photographie, et d’avoir laissé apparaître des ombres qui faussent la perspective.
En fait ce sont les lettres X et Y qui se rapprochent le long de la flèche bleue lorsqu’on plie le soufflet.
On se retrouve alors dans le cas de la photo 2 en fin de post.



ABCD et FBCE sont les deux pièces en bois du soufflet.

La face OAD se rabat sur la OFE , la OAX se rabat sur la OFX, la ODY sur la OEY.
Et de chaque côté du soufflet les deux facettes se rabattent l’une sur l’autre, par exemple XBA sur XBF.

Pendant le pliage/dépliage :
- Pour la partie frontale du soufflet, il n’y a aucune déformation des facettes sur les plis OA, OD, OY, OE, OF, OX.
- Pour les parties latérales du soufflet, il n’y a aucune déformation sur les plis BX et CY.
- Mais il y en a une petite sur les lignes rouges, les plis AX et FX et de l’autre côté sur les plis DY et EY.
Voilà pourquoi j’ai désigné le même point par X et X’ avec X est sur la face latérale et X’ sur la face frontale. Idem pour Y et Y’.

Soufflet fermé on est sur les plis de ces lignes, qui sont ceux faits lors du formage du soufflet. Quand le soufflet est ouvert, on est de nouveau sur le pli de ces lignes.
Mais pendant la manœuvre, la membrane se déplace un peu transitoirement de la partie frontale vers les parties latérales (d’environ 2 où 3 mm). Sur un soufflet en papier ou en cuir on ne remarque rien, mais sur des facettes rigides cela bloquerait.

On calcule très bien, par un peu de trigonométrie, l’amplitude maximale du déplacement.
On peut donc la réduire, en faisant en sorte qu’elle soit nulle en position médiane d’ouverture et qu’elle soit répartie un peu dans un sens, quand on est ouvert, et un peu dans l’autre sens quand on est fermé.
Il suffit de modifier légèrement :
- la forme de la face frontale : déplacer un peu : X et Y vers l’intérieur lorsque le soufflet est fermé
- la forme des faces latérales : avoir un angle BOX qui n’est plus tout à fait un angle droit.

[sh42]

Bonsoir,

Merci SULREN pour cette réalisation. Elle démontre qu'il y a une multitude de manières de réaliser un soufflet et en fonction des dimensions, il y a des résultats différents.

Dans ton cas, il y a un point central et ce sont les points X, X', Y, Y' qui bougent au pliage.
Dans mon cas, il n'y a pas de point central, mais un segment de droite, et les points qui se déplacent se situent au niveau du point O de ton soufflet.

Cela démontre qu'il n'y a pas que les positions ouverte et pliée à prendre en considération, mais également les positions intermédiaires.

Je vais refaire un soufflet avec du carton neuf pour mieux voir ce qu'il se passe.

[SULREN]

Bonsoir,

Je problème dans le soufflet que j’ai montré réside dans le fait que sa partie frontale et ses parties latérales n’ont pas le même rayon de développement.
C'est illustré sur le dessin ci-dessous.
On part d’un point A (ex : soufflet fermé) où les deux rayons arrivent au même point (ou bien les deux arrêtes des faces sont bien bord à bord).
On arrive à un point B (ex : soufflet ouvert) où la situation est la même.

Mais pendant la transition de A à B les deux extrémités des flèches ne peuvent pas être confondues : les deux arrêtes des faces ont tendance à se séparer. Il y a donc blocage si les faces sont très rigides avec des arrêtes maintenues jointives.
Dans le cas de soufflets en papier ou en cuir cela se traduit par un glissement momentané de la membrane d’une face sur l’autre et cela ne se perçoit pas. Il y a cependant une déformation qui fatigue le matériau. Mais si on utilise celui prévu pour cet usage on peut être tranquille pendant des années.

Tu dois avoir un soufflet comme celui ci-dessous (peut-être du type "soufflet d'orgue").

[sh42]

Bonjour,

Non, j'ai un soufflet comme celui de ton post 17.

Mais grâce à tes points X et Y, qui bougeaient, j'ai peut-être trouvé la solution au problème.

Dans nos raisonnements, nous partions du principe que les points X et O se déplaçaient dans plans sur des cercles. Or, dans la réalité et puisque nous sommes en 3D :
* le point X se déplace sur une sphère de rayon FX et une autre de rayon BX,
* un peu pareil, le point O se déplace dans un plan perpendiculaire à la droite FE et également sur la sphère de rayon FO mais on s'en moque un peu de cette sphère car elle est concentrique à celle de FX.
L'intersection de 2 sphères est un cercle.
Dans la résolution pour ne pas avoir de souci, il faut trouver les rayons BX et FX pour que leurs points d'intersection soient situés à une distance OX du plan perpendiculaire à FE.

Si l'on fait un repère orthonormé au point F, tous les points du dit cercle auront une valeur de x ou de y qui seront identiques, d'ou la détermination de BX ou FX suivant que l'un ou l'autre soit déterminé par hypothèse.

[SULREN]

Bonjour,
@SH42: Bonjour et merci du message.

Oh "mille o dioux" , comme on dit par chez moi.
J'ai fait une erreur de raisonnement gravissime, de quoi se faire virer du forum, si les modérateurs ne faisaient pas preuve de mansuétude pour les "vieux" comme moi.

C'est très bien qu'il y ait encore peut-être une possibilité, je tenais vraiment à trouver une forme de soufflet à plaques rigides, jointives, pas pour des raisons pratiques (les soufflets à l'ancienne me suffisent), mais juste comme exercice intellectuel.
Je m'y remet, en écrivant les équations de tout cela en 3D (.....en essayant d'écrire les équations...).
Nous sommes dans le bon forum pour trouver de l'aide.
Quant à la résolution du système d'équations, Mme Méthode Numérique y pourvoira.

[SULREN]

Re,

Quand j’ai écrit dans mon post, #17 :
« Il suffit de modifier légèrement :
- la forme de la face frontale : déplacer un peu : X et Y vers l’intérieur lorsque le soufflet est fermé
- la forme des faces latérales : avoir un angle BOX qui n’est plus tout à fait un angle droit ».


Je pensais à la ligne en rouge sur la photo ci-dessous, mais constituée de deux segments de droite.
Je n’ai pas envisagé une ligne courbe (arc de cercle ou plus complexe). C'est cette courbe qu'il faut trouver.

[sh42]

Bonjour,

Je ne suis pas certain que ce soit une courbe si les dimensions du soufflet sont bien choisies. Sur le coucou que j'ai eu, tout ressemblait à des droites.

Le point O se déplace également sur un cercle dans le plan perpendiculaire à FE.

Dans tout cela, nous avons 2 points remarquables : celui où le soufflet est ouvert et celui où il est refermé car dans les 2 cas les points F, X, O, et le milieu de FE sont dans le même plan.
En partant de la photo du poste 22, je vais essayer de calculer une ou des valeurs de OX qui remplissent les 2 conditions précédentes.

[sh42]

Bonsoir,

@ Sulren, si l'on compte les nombres de carreaux pour BX, BF, OX, XF, FE, il est logique que les points X et Y aient tendance à bouger durant le pliage, car du fait que FX et XO aient la même dimension 9 * 5 = 45 mm, lors du pliage le point X veut venir sur la droite FE et en particulier en son milieu.
Appelons M, le milieu de FE.
Si le triangle BXF est rectangulaire en X, BF^2 = (155^2) + (45^2) soit BF = 161,4 mm
Or, si l'on compte les carreaux nous avons approximativement FX = 45 mm, BX = (31 * 5 ) = 155 mm et BM^2 = (161,4 ^2) + (45^2) soit BM = 167,5 mm. Il manque donc environ 6 mm à BX pour que le pliage se passe bien. Si on diminue la cote OX, on augmente la distance BX et celle de FX.

[SULREN]

Bonjour,
@sh42 :
Bonjour. Je suis désolé de ne pas avoir pu travailler sur ce sujet hier (étant pris par un problème «trivialement matériel » : le remise en état d’une grosse tronçonneuse à bois, datant de 1973 et n’ayant plus tourné depuis 12 ans).
Je voulais calculer dans un repère trois axes la position de X et X’ pendant la variation de l’ouverture du soufflet (X est le point situé sur la face latérale du soufflet et X’ est son vis à vis sur la face frontale du soufflet).
Le comptage des carreaux peut conduire à des calculs trop imprécis pour pouvoir en tirer des conclusions.

J’ai la chance d’avoir le soufflet sous la main et d’observer ce qui se passe
-1) Le pliage du soufflet se fait très bien, il n’y a aucune contrainte qui provoquerait un effet de ressort : voir photo n° 2 de mon post #17.
Dans cette position X et X’ sont confondus, et Y et Y’ aussi, et tous les 4 sont sur le même « segment épais » que A, F, D, E.

-2) Quand le soufflet est presque ouvert en grand (c à d que les deux triangles de chaque face latérale du soufflet sont quasiment dans le même plan) on a de nouveau X et X’ confondus.

-3) Mais en position intermédiaire d’ouverture du soufflet on a BX’ plus long que BX, et CY’ plus long que CY.
L’écart maximum semble atteint vers les 2/3 d’ouverture du soufflet (l'ouverture étant l’angle ABF).

QUESTION: est-il possible d'avoir X et X' toujours confondus pendant l'ouverture du soufflet, en leur donnant une position initiale différente de celle de mes photos actuelles?

Si tu es d'accord prenons comme repère trois axes :
Axe X passant par le milieu de BC et le milieu de FE orienté + de BC vers FE
Axe Y passant par B et C, orienté + de B vers C
Axe Z orthogonal aux deux autres, orienté + vers le haut (sur la photo).

[sh42]

Bonjour,

Merci pour ta réponse.

Pour la mesure par les carreaux, c'est certes imprécis, mais ce n'était que ce que je voyais et avec une différence de 6 mm, un carreau, c'est visible.
Pour le repère 3 axes prendre le milieu de segments comme origine de repère, personnellement, cela me gène car il y a toujours des nombres à " traîner " avec les x, y, z.
Personnellement j'ai pris F comme origine avec FE axe des x, FB axe des y et z vers le plafond. Le soufflet est symétrique par rapport au plan qui passe par le point O et qui est perpendiculaire à FE, AD, et BC.

J'ai la conviction que pour que le pliage se passe bien, les cotes BF, FE, OX, sont liées entre-elles, mais il faut trouver les relations mathématiques.

[sh42]

Bonsoir,

Par pure hasard dans le repère orthonormé d'origine F avec Fx // à FE, Fy // à FB, et Fz perpendiculaire à Fx et Fy, en prenant une valeur de XO = 40 mm, en considérant que X et O se déplaçaient pour O sur un cercle de centre M ( 45, 0, 0 ), avec OM = 45 mm, et pour X sur un cercle de centre I ( 0, 5, 0 ) et pour rayon IX = 45 mm et XO = 40 mm, la longueur FX, soufflet grand ouvert ou fermé est égale à 45,28 mm.

La méthodologie a été la suivante déterminer l'équation du cercle O, déterminer l'équation générale du cercle X, admettre que soufflet ouvert la droite XO était // à Fx, ce qui engendrait que les valeurs Xy, Xz, Oy, Oz étaient identiques 2 à 2, ce qui permettaient de déterminer Xz = Oz = 44,72 mm, avec Xy = Oy = 5 mm.

La longueur BF semble indépendante et être quelconque.

Le point X du soufflet confectionner par Sulren ne peut convenir car FX et BX, lors de la rotation autour de l'axe FB forment 2 cônes et X se déplace sur un cercle perpendiculaire à FB et, soufflet ouvert, du fait de la projection de X sur le plan BFE, X ne peut venir se rabattre sur le point milieu de FE.