Spirales

[Emmanuel Laude]

Bonjour,

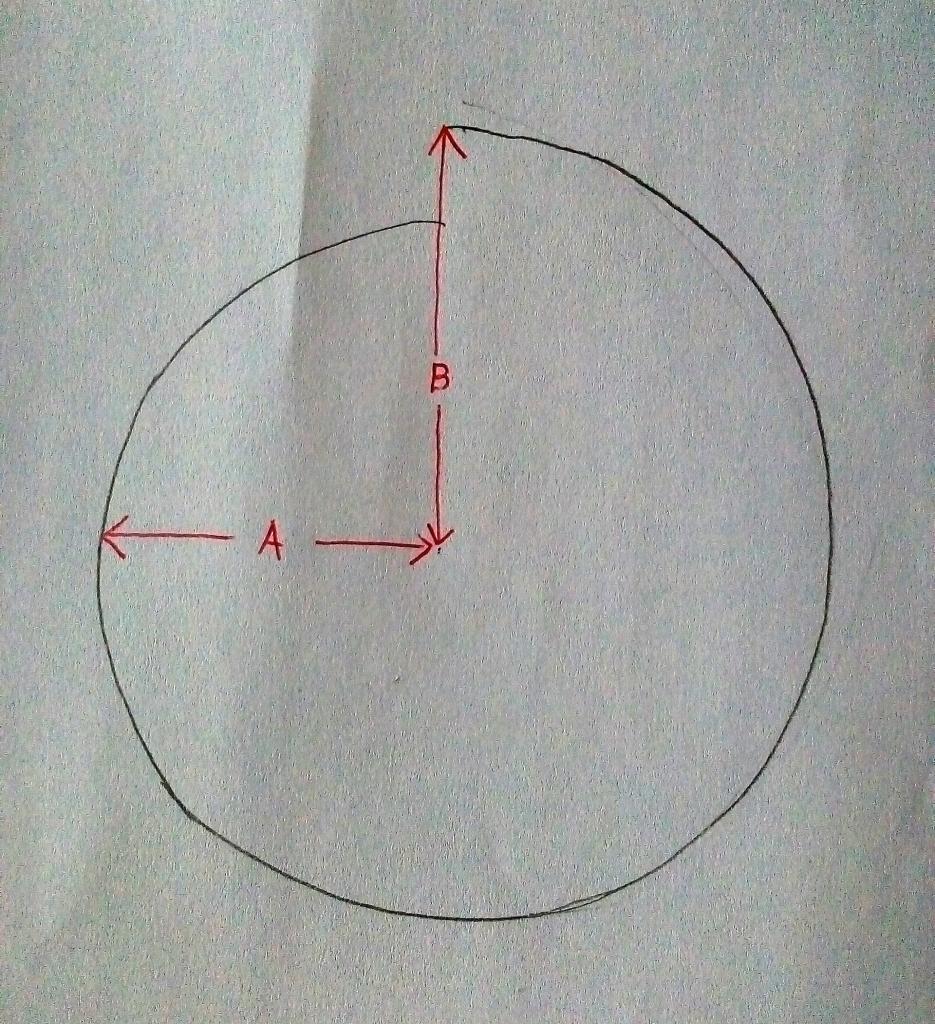
Ne maitrisant pas les termes j’ai fais ce petit dessin. En plus de la réponse à aux trois questions, j’aimerais, si vous l’acceptez, que vous me donniez la bonne terminologie.
Quand A = B nous sommes en présence d’un rond.
Pour qu’il y est spirale il faut que :

1) B = A + x
ou
2) B = A * x

• Quand A/B=1 nous somme en présence d’un rond. Dit-on que la courbure du rond est de 1 ?
• Quelle doit-être la valeur minimum de x pour pouvoir dessiner indéfiniment la spirale de l’extérieur vers l’intérieur sans jamais qu’elle ne se croise elle-même. (pour la façon de calculer 1 et pour la façon de calculer 2) ?
• Quelle est cette valeur pour la spirale de Fibonacci ?

N’hésitez pas à remanier ma façon, probablement exotique, de manipuler ces concepts, en gardant le langage le plus simple et en faisant le moins de référence possible s’il vous plait.

Cordialement,


-----

[Emmanuel Laude]

Je crois avoir compris que je commets une erreur de croire que x doit être supérieur à un minimum pour ne pas que la spirale se croise elle-même. C'est la vision de spirales à centres multiples qui m'a donné cette fausse intuition. N'est-ce pas?

https://fr.wikipedia.org/wiki/Spiral...tres_multiples

[Emmanuel Laude]

Enfin, seulement dans le cas où B = A * x.

[ansset]

re:
il n'y a pas que deux types de spirale, mais une infinité.
les plus connues:
https://fr.wikipedia.org/wiki/Spiral...eux_dimensions
et en général on l'exprime sous la forme d'une ou est l'angle.
on réserve aussi le terme spirale à une fonction croissante de
donc toute fonction croissante convient ( d'où l'infinité )

ici.
-tu compares B à A, cela ne décrit rien à priori sur ce qu'il se passe entre A et B.
-tu n'as que 3/4 de tour entre A et B ce qui rend l'expression peu propre.

cas "B=x+A"
si A était dans l'axe OB, alors une écriture simple serait

r(0)=0 et on rajoute un x à chaque tour.

[A voir en vidéo sur Futura]

[ansset]

ps : "OB=xOA" ne peut démarrer en (0;0) ....
car la multiplication d'un rayon nul reste nul.
en supposant que la spirale commence en (0;1) une solution est
, avec x>1
ainsi si A est le point de départ.



etc, ....

[Emmanuel Laude]

Ah oui, suis-je bête, mon schéma n'est pas bien logique. J'avais fait ça pour avoir quelque part une courbe dans un repair orthonormé mais ce n'était évidement pas une bonne idée. J'ai un peu de mal à comprendre à la fin mais ça ne tiens pas à toi. On va m'aider à interpréter ça.
Merci beaucoup.
Manu

[Emmanuel Laude]

Une de mes questions reste sans réponse.
J'ai supposé que la courbure du rond est égale à un et que celle d'une spirale est supérieure à un mais j'ai du me tromper car j'ai lu que, par convention, une courbure est "forcément positive" pas forcément supérieur à un.

[gg0]

La plupart des spirales ont des courbures variables en fonction du point où on la mesure.
On ne sait toujours pas de quoi tu parles, le mot spirale désignant des courbes très différentes, y compris polygonales, ou constituées d'arcs de cercles.

Cordialement.

[Emmanuel Laude]

La plupart des spirales ont des courbures variables en fonction du point où on la mesure.
On ne sait toujours pas de quoi tu parles, le mot spirale désignant des courbes très différentes, y compris polygonales, ou constituées d'arcs de cercles.

Cordialement.

Ah... Une spirale s'exprime par une fonction alors que la courbure par une valeur... OK

[albanxiii]

Bonjour,

J'ai supposé que la courbure du rond est égale à un et que celle d'une spirale est supérieure à un mais j'ai du me tromper car j'ai lu que, par convention, une courbure est "forcément positive" pas forcément supérieur à un.

Aucune de ces affirmation n'est juste. Où avez-vous appris ou lu tout ça ? Il faut brûler ce livre très vite.

[stefjm]

Brûler un livre, quel qu'il soit est un acte barbare.

[albanxiii]

Outre le fait qu'on pourrait vous donner quelques titres sans lesquels l'humanité se serait mieux portée, oui, je suis un barbare !

[stefjm]

Pour pouvoir combattre une idée, il faut pouvoir la citer.
Brûler le livre ou le mettre à l'index ou le censurer n'est pas une bonne solution.
L'histoire montre bien que cela ne marche pas.

[ansset]

d'autant qu'il ne s'agit pas forcement de son livre:

J'ai supposé que la courbure du rond est égale à un et que celle d'une spirale est supérieure à un mais j'ai du me tromper car j'ai lu que, par convention, une courbure est "forcément positive" pas forcément supérieur à un.

plutôt un pb de compréhension sur la notion de "courbure" , je suppose. ?

[gg0]

Emmanuel Laude,

faire un vrai apprentissage de la géométrie analytique, et donc de la notion de courbe, de tangente, de normale, de rayon de courbure et de courbure ne serait pas de trop si tu veux arrêter de dire n'importe quoi ici. Pour une courbe donnée, suffisamment lisse, et un point précis de cette courbe, le rayon de courbure en ce point est un nombre (ou +oo pour une courbe qui est droite au voisinage de ce point);la courbure en ce point est l'inverse du rayon de courbure (donc 0 pour un segment de droite). Les courbes de courbure constante sont les droites (courbure 0) et les cercles (courbure pour un cercle de rayon ). Les autres courbes ont des courbures variables.

Mais on ne va pas te faire un cours sur la question, prends des bouquins et étudie la question. Sinon, on va de plus en plus se moquer de toi.

Cordialement.