Similitude entre deux lois normales issue de mesures

[invite06be6b3c]

Bonjour à tous.

Déjà merci de me lire et j'espère être dans la bonne section du forum. Voici mon problème : j’aimerai calculer le degré de similitude entre deux lois normales, chacune avec une moyenne et un écart type. Sachant que mes lois sont issue d’observation, je suis donc en mathématique appliquée, avec un problème réel. En clair mes deux lois sont réellement issues de mesures.

Mon but est de déterminer si des échantillons qui proviennent d’un même lot et d’un même fournisseur peuvent être considérer comme homogènes entre eux, selon un critère d’évaluation. En d’autres termes, peuvent-ils être considérés comme tous identiques avec un faible risque d’erreur ou doit-on les analyser un par un ?

Pour cela j’ai effectué 12 mesures par échantillons en différents points de mesure avec un appareil sur un petit lot de 30 échantillons. J’obtiens donc une moyenne globale pour ma population (30), mais surtout une moyenne et un écart type pour chacun échantillons, issus de mes 12 mesures. Sauf erreur de ma part, j’ai donc à la fois mon potentiel de variabilité entre chaque échantillon additionné avec mon erreur de mesure, lié à l’appareil. Comment déterminer si mes échantillons sont tous identiques (l’écart observé ne provient que de l’appareil, sachant que je n’ai que 12 mesures) ou ils présentent bien des écarts entre eux, et c’est ce qui est mis en évidence par mes mesures ?

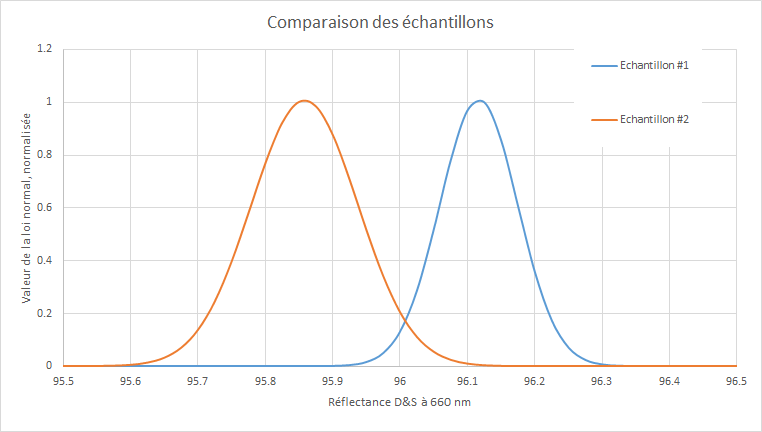
Personnellement, j’ai sélectionné les deux extrêmes : celui avec la plus haute moyenne et celui avec la plus base. Mon but est de prouvé qu'ils ne sont pas identique, afin d'invalidé l'hypothèse que tout mes échantillons le sont. Donc avec leurs moyenne et écarts types, j’ai pu tracer leurs lois normales respectives. Elle se croise à leurs extrémités. Je vous mets le graphique.

Et après je sèche. J’aurais tendance à conclure que les deux échantillons sont bien différents, mais j’aimerais le quantifier. Quelqu’un aurait une méthode ?

Merci !!

-----

[gg0]

Bonjour.

Si on suppose que l'instrument de mesure donne des valeurs avec une éventuelle erreur gaussienne et que chaque échantillon a des mesures "vraies" réparties suivant la loi Normale, on peut utiliser les tests classiques (Student, dit aussi t-test) de comparaison de moyennes. Comme il s'agit de méthodes très connues, mais qu'un forum n'est pas fait pour présenter un cours de statistiques inférentielles, je t'invite à lire un ouvrage de statistiques où ces notions sont exposées (il vaut mieux avoir étudié, même seul, la théorie des tests d'hypothèse avant d'en pratiquer).
A vue de nez, aux risques habituels, tes deux échantillons sont significativement différents.

Cordialement.

[invite06be6b3c]

Merci de votre réponse !
Impec, avec votre aide j'ai les mots clefs nécessaires et je sais maintenant quoi chercher.
Je me lance donc dans les cours nécessaires.

Pour information et éventuellement laissé une trace pour les suivants j'ai fait le test suivant :
Si mes échantillons sont homogènes alors toutes les valeurs mesurées (12 par échantillons, 360 au total) sont normalement indépendantes de l’échantillon. Donc quand je mesure un échantillon avec une moyenne très éloignée de la moyenne de la population sur 12 mesures cela voudrait dire que j’ai eu 12 fois ‘pas de chance’ et que c’est mon appareil qui m’a donné à chaque fois un signal presque en dehors de sa plage de mesure. J’ai donc fait un petit code qui tire au hasard 12 mesures parmi les 360 disponibles et qui recalcule moyenne et écart type pour chaque échantillon ‘artificiel’. En étudiant le résultat d’un grand nombre de lancers (> 1000) j’ai comparé la répartition des résultats obtenue ‘artificiellement’ avec celle que j’obtenais réellement.
La loi normale est beaucoup plus serrée. Si on élimine les cas avec une probabilité très faible (inférieur à 1 sur 10^6) elle n’intègre plus les mesures réelles de plusieurs de mes 30 échantillons. En conclusion, si mes échantillons sont homogènes, je n’avais presque aucune chance d’obtenir ces résultats. J’en conclus donc qu’ils ne le sont pas.