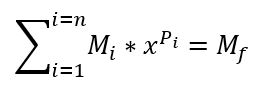Calcul intérêt sur placement

[a3jeu04]

Mise en situation

Il y a 5 ans, j'ai mis 2000$ dans un placement dont je ne connais pas l'intérêt, que nous allons nommer x.

Il y a 3 ans, j'ai remis 3000$ dans ce même placement à taux x.

Il y a 1 an, j'ai remis 1000$ dans ce placement.

Aujourd'hui, la somme de tous mes placements valent 8000$. Je cherche à savoir quel était le taux d'intéret annuel.

Démarche

Je peux établir l'équation 2000*x⁵ + 3000*x³ + 1000*x¹=8000

ou

M₁*x^P₁ + M₂*x^P₂ + M₃*x^P₃ = M_F

ou




avec :

x : Le montant de l'intéret qu'on cherche;

M_i : Les montants d'argent investis

M_F : La valeur du placement en date d'aujourd'hui

P_i : La durée à laquelle le montant a été appliqué au taux d'intéret X.

Je n'arrive pas à résoudre cette équation. Quelqu'un peut m'aider ?

Merci
-----

[ansset]

A priori, il n'y a pas de solution analytique ( équation du 5 ème degré ).
Néanmoins ce que tu nommes x est en fait 1+t ( ou t est le taux)
ce qui revient à
2(1+t)⁵+3(1+t)³+(1+t)=8
si on suppose t<<1 en première intention, on peut faire l'approximation (1+t)ⁿ equiv 1+nt.
l'équation devient après simplification
20t=2 soit t=0,1
on sait donc que ce n'est qu'un résultat approximatif car t n'est pas négligeable devant 1.

pour avoir une solution plus précise , on peut recourir à la méthode de Newton.
( qui revient à itérer le croisement de la tangente à la courbe avec l'axe des abcisses )
soit pour simplifier :
prendre une valeur proche du résultat, soit x₀
puis la suite x_n+1=x_n-f(x_n)/f'(x_n)

ici , on peut revenir au x recherché ( x=1+t)
f(x)=2x⁵+3x³+x-8=0
f'(x)=10x⁴+9x²+1
avec x₀=1+t₀=1+0,1=1,1
au bout de 3 itérations on trouve
x=1,08796649

[jacknicklaus]

on peut aussi faire un développement à l'ordre 2 ce qui donne 29t² + 20t - 2 = 0 soit t = 0.0088.
Naturellement, c'est moins précis que par NEwton.

[ansset]

En fait, je trouve ça même mieux, j'aurai du le mentionner, mais maintenant c'est fait

[A voir en vidéo sur Futura]

[ansset]

En fait, je trouve ça même mieux

mieux, parce qu'on sait que t est de l'ordre de 0,1, donc t² est de l'ordre de 10^(-2) et peut être lui considéré comme négligeable devant 1.
d'ailleurs le résultat obtenu avec un DL à l'ordre 2 le confirme. ( à part la petite faute de frappe 0,088 )

[pm42]

A priori, il n'y a pas de solution analytique ( équation du 5 ème degré ).

En effet, c'est le calcul du TRI, taux de rendement/rentabilité interne et Newton est une bonne solution.

C'est aussi disponible en Excel : https://support.office.com/fr-fr/art...0-3ad0c163c1bc
J'ai vu des cas où cela ne fonctionnait pas toutefois.

Et c'est la fonction IRR des calculatrices financières comme les HP-12C.