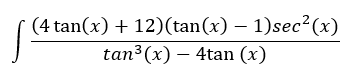Bonjour les gens,
J'ai quelques difficultés avec ce numéro:
J'ai essayé d'établir u=tan(x), du=ln(sec(x)), mais cela ne rentre pas dans la fonction.
J'ai essayé d'établir u=sec*2(x), du=tan(x), mais je ne sais pas comment l'utiliser dans la fonction (Est-ce que tout les tan(x) seraient supprimé? ou seulement celui présent au dénominateur (lors de la factorisation)?)
J'ai même essayer de factoriser et « défactoriser » la fonction mais je suis toujours bloqué.
Merci de votre aide
Bonjour.
Tu peux facilement exprimer ta fonction à l'aide uniquement de tan(x), et faire le changement de variable u=tan(x).
Cordialement.
NB : "u=tan(x), du=ln(sec(x))," ???? très bizarre !!
NBB : "intégrale" est du féminin.
Dernière modification par gg0 ; 21/04/2020 à 08h40.
Wolfram en deux secondes plus les cinq minutes nécessaires pour entrer l'intégrale sans erreurssss
https://www.wolframalpha.com/input/?...3%28x%29%29+dx
Formules en t = a/2 ??? et beaucoup de calme, de patience et de persévérence des fois que ça ne marcherait pas
Sejam
Salut,
Sont marrants ces exercices de math ! Si comme moi tu as eu peur de la sec², c'est que tu as oublié la dérivée de la tgEnvoyé par gg0
Il y a du sadisme dans ces énoncés
Biname
Ah, effectivement,
mais je n'ai jamais utilisé sec et cosec, qui ne font que rajouter des noms. On n'en avait même pas besoin pour les calculs avec les tables de logarithmes. La cotangente est en train de disparaître dans l'enseignement, pour les mêmes raisons.
Cordialement.
Donc on pose u=tan(x), du=sec²(x)? On remplace tous les tan(x)? même ceux au dénominateur?
ben forcement !
sinon c'est du=sec²(x)dx.
Plus précisément :
u=tan(x), sec²(x) dx = du
et on applique la méthode de changement de variables dans les intégrales.
On se retrouve face à une intégrale de fraction rationnelle qu'on traite par la méthode habituelle (factoriser le dénominateur, décomposer en éléments simples).
Cordialement.
Est-ce normal que cela me donne une réponse hyper longue?
Ça me donne: 2 ln(tan²(x)-4) +4ln(tan²(x)-4) + 3ln(tan(x)) - 3/2 ln(tan²(x)-4) + C
re-
tes termes en ln(tan²(x)-4) se regroupent.
mais même si..... ce n'est pas le bon résultat
si tu détailles tes calculs , on y verra l'erreur, qui ne doit pas être énorme.
en fait tu as du voir qu'on est ramené à "intégrer" ( à un facteur 4 près ):
(x+3)(x-1)/(x^3-4x) à décomposer
ps : je ne l'ai pas fait moi même , je déteste les calculs dès qu'ils un peu lourds.... faignant avec l'age
Salut,
Wolfram donne un résultat prochedu tien ? Qui se trompe et où ?
après u = tg(x) et du= sec²(x) dx et dx = 1/sec²x (quelle chance on a!)
sauf erreur de ma part, il reste : integ (4u²+8u-12)/(u³-4u) du
Wolfram apart (4u²+8u-12)/(u³-4u) = 5/(2 (-2 + u)) + 3/u - 3/(2 (2 + u))
Wolfram integ (5/(2 (-2 + u)) + 3/u - 3/(2 (2 + u)))du = 4 log(2 - u) + 3 log(u) - 3/2 log(4 - u^2) + Cste
Wolfram 4 log(2 - u) + 3 log(u) - 3/2 log(4 - u^2) + Cste and u=tg(x)
donne 4 log(2 - tan(x)) + 3 log(tan(x)) - 3/2 log(4 - tan^2(x))
Biname
ben juste que wolfram donne un résultat différent du tien, pas du mien.Wolfram donne un résultat proche
ps : j'ai le confinement faignant je t'ai dit.
Biname,
4-u²=(2-u)(2+u)
ce qui fait que tu as à prendre u=tan(x) dans 3 ln(u)+5/2ln(2-u)-3/2ln(2+u)
C'est bien gentil d'utiliser les services d'un calculateur formel, encore faut-il savoir quoi faire du résultat, qui peut s'écrire de différentes façons. Et tout ça ne règle pas le problème de Lilponey, qui doit apprendre à trouver sans calculateur formel. Et pour l'instant s'est trompé.
Cordialement.
Salut,
On ne va pas sortir du sujet ! Il n'était pas loin de la solution Lilponey.
Biname 65 ans
En maths, "pas loin" s'appelle faux.
Et Lilponey n'est pas revenu (peut-être est-il content de copier le résultat juste sans être capable de le trouver).
Enfin je te rappelle (voir https://forums.futura-sciences.com/m...ces-forum.html) que la règle sur ce forum n'est pas de donner des solutions ou des corrigés, mais d'aider les gens qui ont des exercices à faire à les faire eux-mêmes.
Cordialement.
