Fibonacci, Padovan, Binet

[plaplat]

Bonjour,

J'ai trouvé ce document qui m'a donné un fonction qui a pour solution la suite de Fibonacci.

Connaissez-vous une fonction qui fait la même chose pour la suite de Padovan ?


PS : J'ai bêtement remplacé φ(nombre d'or) par Ψ(nombre plastique) mais la courbe ne s'annule pas suivant la suite de Padovan.
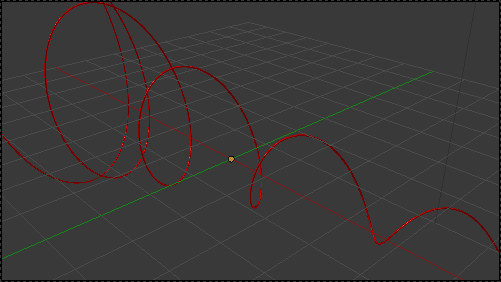
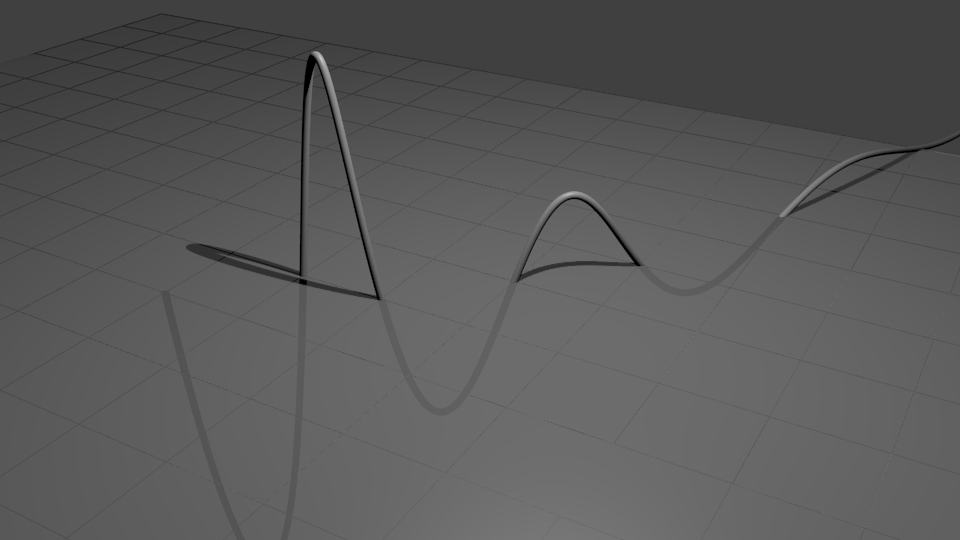
La courbe coupe le plan en suivant la suite de Fibonacci

-----

[Médiat]

Bonjour,

Votre réponse se trouve dans l'article de wikipedia https://fr.wikipedia.org/wiki/Suite_de_Padovan, il suffit de remplacer n par x dans l'expression de Pn (mais avec des calculs dans les complexes)

[plaplat]

Merci pour la rapide réponde.

Peut-être ais-je mal compris. Pouvez-vous me confirmer que la fonction P(n) pour n entier me donne la suite de Padovan ?

Avec ton aide et l'article nombre plastique
J'obtiens :
avec
où,






où,








J'ai programmé la fonction en python sur Blender3D mais je ne retrouve pas la suite de Padovan sur le plan cartésien. Voyez-vous mon erreur ?
Mon programme me donne les valeurs numérique:



Et ,

Une visualisation 3D:

Le script python3

import math
from math import sqrt
import cmath 

class Padovan:
    class Polynomial:
        def roots():
            a = pow(27/2-3*sqrt(69)/2, 1/3)/3
            b = pow(1/2*(9+sqrt(69)), 1/3)/pow(3, 2/3)
            z1=complex(1, -sqrt(3))
            z2=complex(1, sqrt(3))
            r1 = a + b
            r2 = -z1*a/2 - z2*b/2
            r3 = -z2*a/2 - z1*b/2
            return (r1, r2, r3)

r1, r2, r3 = Padovan.Polynomial.roots()
for n in range(0, 5):
    a = (1-r2)*(1-r3) / (r1-r2)*(r1-r3) * pow(r1, n)
    b = (1-r3)*(1-r1) / (r2-r3)*(r2-r1) * pow(r2, n)
    c = (1-r1)*(1-r2) / (r3-r1)*(r3-r2) * pow(r3, n)
    p = a + b + c
    print(p.real)

output :

2.4999999999999996
3.9999999999999982
3.9999999999999987
6.4999999999999964
7.999999999999995

Or, je m'attendais à :

1
1
1
2
2

[plaplat]

Il manquait des parenthèses...
a = (1-r2)*(1-r3) / ((r1-r2)*(r1-r3)) * pow(r1, n)

[A voir en vidéo sur Futura]

[plaplat]

Il semblerai qu'avec la fonction P(n) de wikipedia la partie imaginaire s'annule.

Du coup j'obtiens un courbe plate et pas en 3D comme je l'aurai souhaité.

Pour Fibonacci, dans un espace 3D, j'avai :
t € R
F(t) = (pow(phi, t) - pow(-1, t)*pow(phi, -t))/math.sqrt(5)

x(t)=t
y(t)=Re(F(t))
z(t) = Im(F(t))

Si vous avez d'autre info au sujet de Padovano je suis preneur

PS: Merci encore Médiat pour votre aide précieuse. Je n'avais pas du tout pensé que la fonction que vous m'avez indiqué puisse faire d'aussi belle chose( Petit bonus, j'ai eu une belle surprise en me trompant dans les parenthèse)

[Médiat]

Il semblerai qu'avec la fonction P(n) de wikipedia la partie imaginaire s'annule.

Pour le entier, oui, c'est l'idée, mais pour tout x, je serait surpris

[plaplat]

Merci vraiment pour l’intérêt que vous portez a ma question et le temps que vous me consacrez, et l'aide que vous me prodigué

J'ai refait les calculs à la main. je m'aperçoit que si on écrit:
P(n) = z1 * r1^n + z2 * r2^n + z3 * r3^n
Alors z1 est un réel, et z2 est le conjuguer de z3

Si on écrit :
P(n) = Za + Zb + Zc
Alors Za est un réel pure, et Zb est le conjuguer de Zc. Je me l'explique en disant que r2 est le complexe conjuguer de r3 et l'élevé a la puissance n ne change rien a l'affaire.

Lorsque l'on somme Zb + Zc la partie imaginaire s'annule.

Ce qui me fascine c'est que si r2 et r3 ne sont pas des complexe conjuguer alors j'obtiens de belle courbe spirale elliptique en 3D

[jacknicklaus]

r2 est le complexe conjuguer de r3 et l'élevé a la puissance n ne change rien a l'affaire

Attention, c'est tout l'inverse

r2 est le complexe conjugué de r3 et l'élever a la puissance n ne change rien a l'affaire

[Médiat]

j'obtiens de belle courbe spirale elliptique en 3D

Si elles sont jolies, postez-les ...

[plaplat]

Ici r3 est le complexe conjugué de r2
padovan-0.png

Ici j'ai augmenté r2 avec i0.5
padovan-r2-0_5.png

Ici j'ai augmenté r2 avec i1.0
padovan-r2-1_0.png


Ici j'ai augmenté r2 avec i1.5
padovan-r2-1_5.png

Ici j'ai augmenté r3 avec i0.5
padovan-0_5.png

PS: jacknicklaus promis je vais faire attention à mon orthographe dorénavant

[jacknicklaus]

très joli. le padovan-0_5.png est superbe.

tu peux partager un de tes scripts ? Ca me donne envie de tester Blender.

[plaplat]

Okay promis je partagerai. Le script est en chantier complet.... laisse moi un peu de temps pour faire le ménage et apporter un peu de consistance.


Pour assouvir ta curiosité, voici ce que j'ai "trouvé" (?) sur une feuille de vigne :
vigne-nervure.png les premières nervure suivent la suite de Fibonacci, et la nervure principe suit la suite de Padovan. J'ai trouver encore d'autre concordance mais ca reste spéculatif...
10618731-feuille-de-vigne-isol%u0025C3%A9.jpg

 Cliquez pour afficher

script pour Fibonacci. Pour executer le script taper Alt+p

import math

# TODO create mesh instead of data array
# see: https://docs.blender.org/api/current...ypes.Mesh.html
# Fibonacci.Triangle.create_mesh()

class Fibonacci:
    GOLDEN_RATIO=1.6180339887
    def __init__(self):
        foo = 0
    # __iter__, __next__
    # use iterator: for FFn in Fibonacci(0, 10):
    class Sequence:
        class Inner:
            def foo(self):
                return 1
        def __recursive(self, n):
            if n < 0:
                return pow(-1, n+1) * self.__recursive(-n)
            elif n == 0:
                return 0
            elif n == 1:
                return 1
            else:
                return(self.__recursive(n-1) + self.__recursive(n-2))
        def __memoize(self, f):
            memo = {}
            def helper(x):
                if x not in memo:            
                    memo[x] = f(x)
                return memo[x]
            return helper
        def F(self, n):
            if type(n) != int:
                raise TypeError("n must be an integer")
            #if n < 0:
            #    raise TypeError("n must be positive")
            #return self.__recursive(n)
            helper = self.__memoize(self.__recursive)
            return helper(n)
    class Polynomial:
        def f(x):
            return x**2 - x - 1
        def roots():
            r = (1 - sqrt(5)) / 2
            return r
    class Curve:
        def cFs(x):
            return 0
        def sFs(x):
            return 0
        def FF(x):
            return 0
    #triangular golden spiral
    #class Triangle:
    #class Rectangle:
    #class Spiral:
    #class Shofar:
    # register...
    # bpy.ops.mesh.primitive_cube_add()
    # register...
    # bmesh.ops.create_cube(bm, size=1.0)
    #def create_plane(location=(x,y,z),size=1, repeat=2)
    #def create_cube(location=(x,y,z),size=1, repeat=2)
    #class Spiral:
    class Triangle:
        def create_plane():
            a = Fibonacci.GOLDEN_RATIO/2.0
            c = 1.0
            b = math.sqrt(1.0 - a*a)
            verts = [
                (-a, 0.0, 0.0),
                ( a, 0.0, 0.0),
                ( 0.0, b, 0.0)
            ]
            edges = [
                (0, 1),
                (1, 2),
                (2, 0)
            ]
            faces = [
                (0, 1, 2)
            ]
            return [verts, edges, faces]
    class Rectangle:
        def create_plane():
            a = 1.0
            b = 2.0/Fibonacci.GOLDEN_RATIO + 1.0
            verts = [
                (-1.0, 1.0, 0.0),
                ( b, 1.0, 0.0),
                ( b, -1.0, 0.0),
                ( -1.0, -1.0, 0.0)
            ]
            edges = [
                (0, 1),
                (1, 2),
                (2, 3),
                (3, 0)
            ]
            faces = [
                (0, 1, 2, 3)
            ]
            return [verts, edges, faces]



"""
fib = Fibonacci.Sequence()
print(fib.F(-1)) => 1
print(fib.F(0))  => 0
print(fib.F(1))  => 1
print(fib.F(2))  => 1
print(fib.F(3))  => 2
print(fib.F(4))  => 3
print(fib.F(5))  => 5
"""



"""
#OK
def binet(min, max, step):
    delta = (max-min)/step
    verts=[]
    edges=[]
    faces=[]
    for n in range(0, step):
        t = min+n*delta
        w=(1+math.sqrt(5))/2.0
        
        x=t
        y = (pow(w, t) - pow(-1, t)*pow(w, -t))/math.sqrt(5)
        z = 0.0
        crd = (x, y.real, z)
        verts.append(crd)
        if n > 0:
            edges.append( (n-1, n) )
    return (verts, edges, faces)

data = binet(-10, 10, 128)
verts = data[0]
edges = data[1]
faces = data[2]
"""

"""
# OK golden shofar function
def quasi_sine_Fibonacci(min, max, step):
    delta = (max-min)/step
    verts=[]
    edges=[]
    faces=[]
    for n in range(0, step):
        t = min+n*delta
        w=(1+math.sqrt(5))/2.0
        
        x=t
        y = (pow(w, t) - pow(-1, t)*pow(w, -t))/math.sqrt(5)
        z = y.imag
        crd = (x, y.real, z)
        verts.append(crd)
        if n > 0:
            edges.append( (n-1, n) )
    return (verts, edges, faces)

data = quasi_sine_Fibonacci(-10, 10, 128)
verts = data[0]
edges = data[1]
faces = data[2]
"""


"""
#OK
def hyperbolic_sin(min, max, step):
    delta = (max-min)/step
    verts=[]
    edges=[]
    faces=[]
    for n in range(0, step):
        t = min+n*delta
        w=(1+math.sqrt(5))/2.0
        
        x=t
        y = (pow(w, t) - pow(w, -t))/math.sqrt(5)
        z = 0.0
        crd = (x, y.real, z)
        verts.append(crd)
        if n > 0:
            edges.append( (n-1, n) )
    return (verts, edges, faces)

data = hyperbolic_sin(-7, 7, 32)
verts = data[0]
edges = data[1]
faces = data[2]
"""



"""
#OK
def hyperbolic_cos(min, max, step):
    delta = (max-min)/step
    verts=[]
    edges=[]
    faces=[]
    for n in range(0, step):
        t = min+n*delta
        w=(1+math.sqrt(5))/2.0
        
        x=t
        y = (pow(w, t) + pow(w, -t))/math.sqrt(5)
        z = 0.0
        crd = (x, y.real, z)
        verts.append(crd)
        if n > 0:
            edges.append( (n-1, n) )
    return (verts, edges, faces)

data = hyperbolic_cos(-7, 7, 32)
verts = data[0]
edges = data[1]
faces = data[2]
"""


"""
def binet(min, max, step):
    delta = (max-min)/step
    verts=[]
    edges=[]
    faces=[]
    for n in range(0, step):
        t = min+n*delta
        w=(1+math.sqrt(5))/2.0
        
        x=t
        y = (pow(w, t) - pow(-1, t)*pow(w, -t))/math.sqrt(5)
        z = 0.0
        crd = (x, y.real, z)
        verts.append(crd)
        if n > 0:
            edges.append( (n-1, n) )
    return (verts, edges, faces)


import bpy

def main():
    data = binet(-10, 10, 128)
    verts = data[0]
    edges = data[1]
    faces = data[2]
    mesh_data = bpy.data.meshes.new("segment_mesh_data")
    mesh_data.from_pydata(verts, edges, faces)
    mesh_data.update()
    obj = bpy.data.objects.new("My_Object", mesh_data)
    scene = bpy.context.scene
    scene.objects.link(obj)
    scene.objects.active = obj
    obj.select = True
"""

"""
def quasi_sine_Fibonacci(min, max, step):
    delta = (max-min)/step
    verts=[]
    edges=[]
    faces=[]
    for n in range(0, step):
        t = min+n*delta
        w=(1+math.sqrt(5))/2.0
        
        x=t
        y = (pow(w, t) - pow(-1, t)*pow(w, -t))/math.sqrt(5)
        z = y.imag
        crd = (x, y.real, z)
        verts.append(crd)
        if n > 0:
            edges.append( (n-1, n) )
    return (verts, edges, faces)

import bpy

def main():
    data = quasi_sine_Fibonacci(-10, 10, 1024)
    verts = data[0]
    edges = data[1]
    faces = data[2]
    mesh_data = bpy.data.meshes.new("segment_mesh_data")
    mesh_data.from_pydata(verts, edges, faces)
    mesh_data.update()
    obj = bpy.data.objects.new("My_Object", mesh_data)
    scene = bpy.context.scene
    scene.objects.link(obj)
    scene.objects.active = obj
    obj.select = True
    


if __name__ == '__main__':
    main()
"""


from math import cos, sin, pi

def FibonacciSpiral3D(min, max, step):
    delta = (max-min)/step
    verts=[]
    edges=[]
    faces=[]
    phi = 1.6180339887 # Fibonacci.GOLDEN_RATIO
    for n in range(0, step):
        t = min+n*delta
        x=t
        y = (pow(phi, t) - cos(math.pi*t)*pow(phi, -t)) / math.sqrt(5)
        z = (sin(math.pi*t)*pow(phi, -t)) / math.sqrt(5)
        crd = (x, y, z)
        verts.append(crd)
        if n > 0:
            edges.append( (n-1, n) )
    return (verts, edges, faces)

import bpy

def main():
    data = FibonacciSpiral3D(-10, 10, 1024)
    verts = data[0]
    edges = data[1]
    faces = data[2]
    mesh_data = bpy.data.meshes.new("segment_mesh_data")
    mesh_data.from_pydata(verts, edges, faces)
    mesh_data.update()
    obj = bpy.data.objects.new("My_Object", mesh_data)
    scene = bpy.context.scene
    scene.objects.link(obj)
    scene.objects.active = obj
    obj.select = True
    


if __name__ == '__main__':
    main()