Courbe à rayon progressif ou ellipse...
Discussions similaires
-
Par invited6b2ac16 dans le forum Chimie
Réponses: 3
Dernier message: 23/05/2014, 20h10
-
Par inviteb0547c5a dans le forum Mathématiques du supérieur
Réponses: 2
Dernier message: 04/10/2011, 08h58
-
Par invitefb730b1b dans le forum Mathématiques du collège et du lycée
Réponses: 3
Dernier message: 20/11/2008, 00h24
-
Par Bleyblue dans le forum Mathématiques du supérieur
Réponses: 20
Dernier message: 20/05/2005, 21h29
-
Par Bleyblue dans le forum Mathématiques du supérieur
Réponses: 10
Dernier message: 24/11/2004, 01h21
[ATTACH




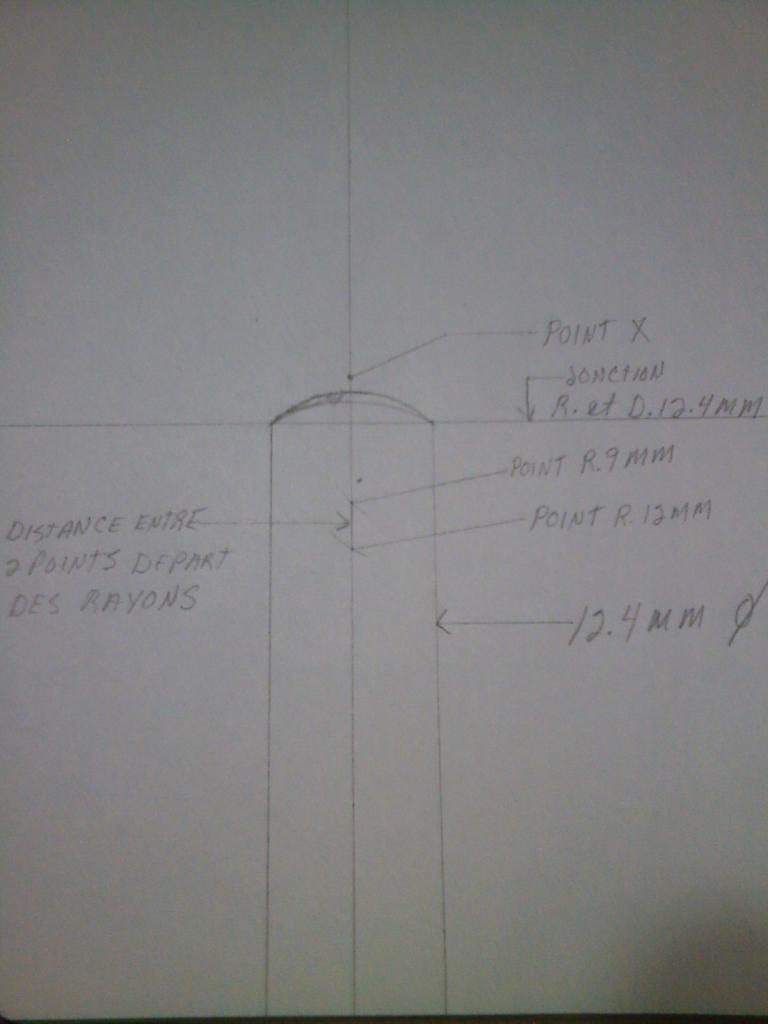

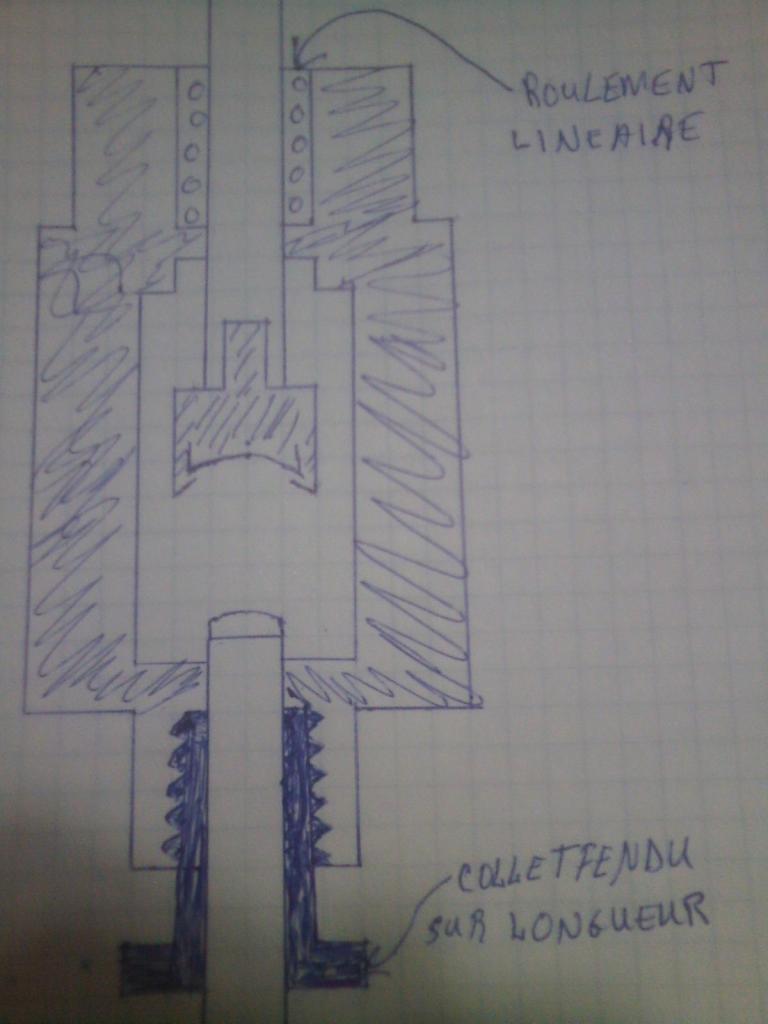
 Merci!
Merci!