Transformation de Fourier

[Mina mia]

Salut
J'ai cet intégrale à calculer et j'ai trouvé un problème dans la dernière partie
Merci d'avance.

-----

[gg0]

Bonjour.

Je n'ai pas compris pourquoi tu fais un changement de variable au début, alors que tu peux directement écrire comme un produit de convolution. Et tu oublies les bornes dans le changement de variables, puis miraculeusement tu oublies le - ensuite ce qui rectifie l'erreur.

Ensuite, je ne comprends pas bien comment tu procèdes, même si je comprends ton intension. Et à la fin, tu as un résultat qui est effectivement bizarre, mais c'est normal : nulle part tu n'as utilisé la vraie valeur de h. Par exemple, deuxième page, troisième ligne, tu n'utilises pas h mais apparemment g.

Cordialement.

[Mina mia]

Merci beaucoup.
J'ai vraiment mélangé les choses
En fait j'ai utilisé g au lieu de h (c'est faute de déconcentration)
https://image.noelshack.com/fichiers...003-190409.jpg
Et pour f est ce que je dois faire un changement de variable ou je calcule directement (dans cas je trouve la même résultat que g mais avec 5 pi au lieu de 6 pi)??
Merci une deuxième fois.

[gg0]

Heu ... tu devrais déjà regarder ce qu'est f(x) (ou f(u), voire f(u)) pour pouvoir traiter le produit de convolution de f par g (il n'y a plus de u). Et oui, c'est presque déjà fait !

[A voir en vidéo sur Futura]

[Mina mia]

On a f (t-u)=(sin (5 (t-u)))/(t-u)
J'ai pas compris ce que vous avez dit sur f ??

[gg0]

f:= x --> f(x) =

Tu fais de la convolution, du Fourier, et tu ne fais pas encore la différence entre la fonction f et le nombre f(t-u) ?

J'ai fait une erreur de touches, c'est "ce qu'est f(x) (ou f(t), voire f(u))"

[Mina mia]

Comma ça??

[gg0]

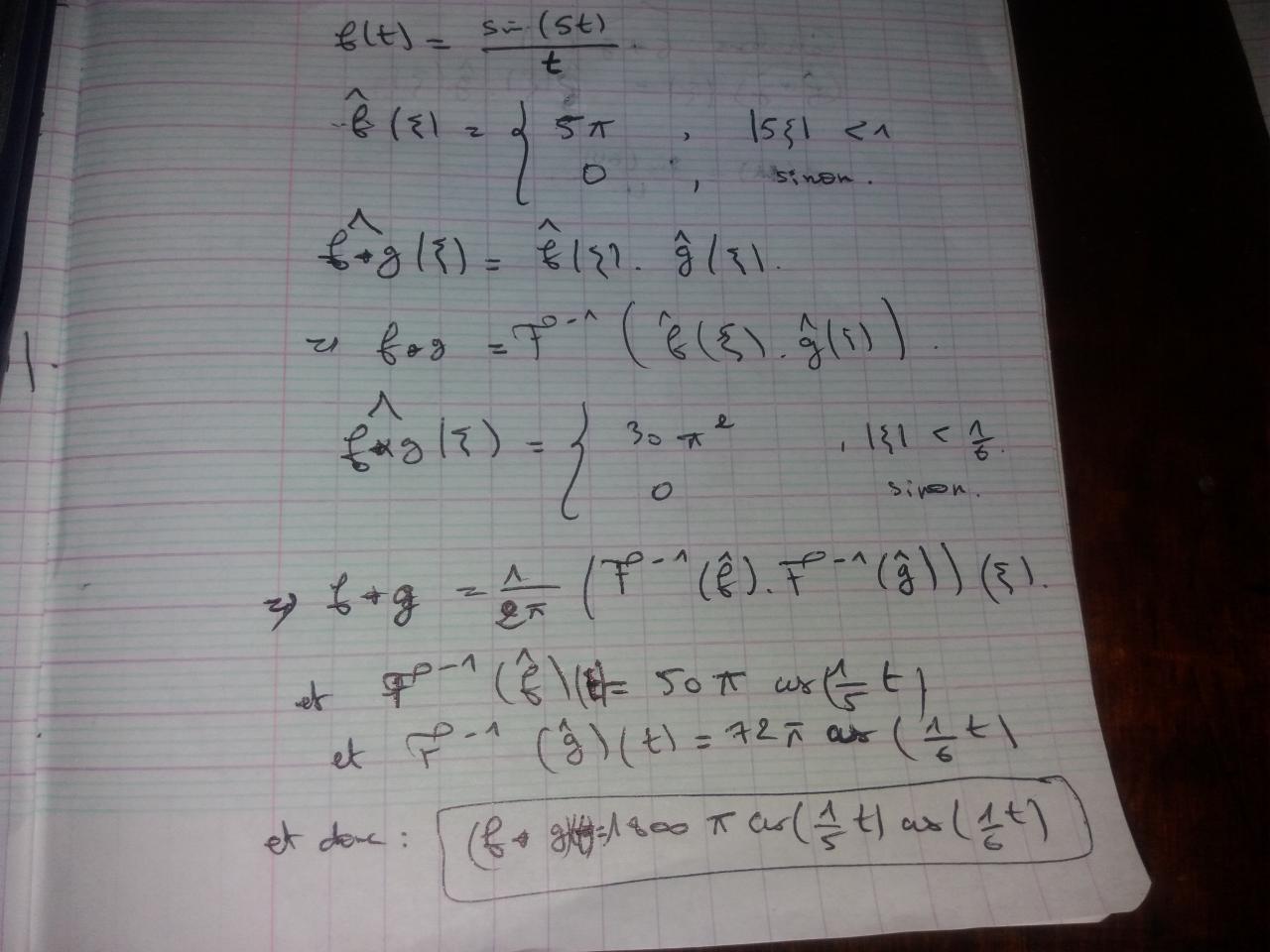
Je ne comprends pas les 4 dernières lignes, on dirait que tu tournes en rond.
Tu as trouvé la TF de f*g, et c'est une fonction élémentaire dont tu peux facilement trouver l'antécédent par Fourier (tu as déjà fait ça dans l'autre sens deux fois). Pourquoi réutilises-tu la formule qui t'a fait arriver ici et de travers en plus ? Tu crois vraiment que f*g est proportionnel à f.g ??? En fait, à la première de ces 4 lignes, c'est un produit de convolution, et c'est ce que tu dis depuis le début !!

[Mina mia]

Vous avez raison ,je l'ai réctifié .
Merci beaucoup pour votre aide.