Oscillateur harmonique

[tin123tin]

Bonjour, je vais intégrer à la rentrée une classe de MPSI, j'ai donc décider de m'avancer un peu sur le programme car j'ai vu qu'en physique nous commencions avec l'oscilateur harmonique.
J'ai donc consulter un cours sur internet mais il me semble qu'il y a une erreur ou alors je n'ai pas compris (voir pièce ci-jointe).


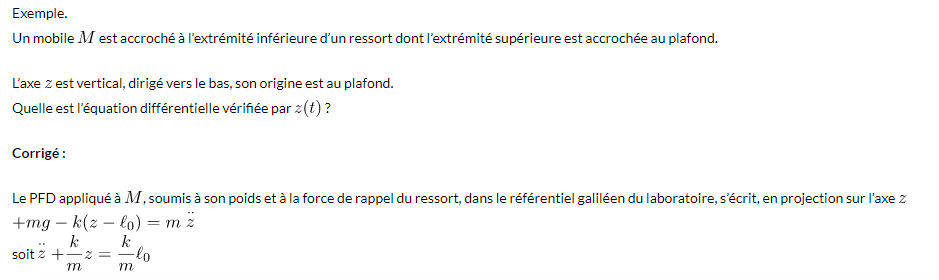
Vu qu'on est sur un axe vertical orienté vers le bas nous avons bien : mg-k(z-l0)=m (z̈)

donc: mg-kz+kl0=m (z̈)
: g-kz/m+kl0/m= (z̈)
: ( z̈) +kz/m=kl0/m+g
Ai-je fait une erreur ?
-----

[invite18230371]

Bonjour,

Non, c'est d'ailleurs la même chose que le corrigé...

(...)dans le référenciel supposé galiléen du laboratoire,(...)

[gg0]

Non,

il manque bien le g dans le corrigé.

Cordialement.

[tin123tin]

Merci de vos réponses mais si je comprend bien vos réponses, d'apres StrangQuark étant donné que nous sommes dans le référentiel supposé galiléens le "g" est négligeable dans l'équation.
D'apres g00 il manque le "g".
Dois-je comprendre que le "g" est négligeable car nous sommes dans le référentiel galiléens mais que par un souci de rigueur il est préférable de l'intégrer à l'équation ?

(Je manque de rigueur je dois améliorer cela avant de rentrer en sup ma question est peut être stupide)
Cordialement.

[A voir en vidéo sur Futura]

[gg0]

J'ai répondu sans voir la réponse de StrangeQuark; que je ne comprends d'ailleurs pas (en quoi le fait que le référentiel soit galiléen changerait la valeur de g. D'ailleurs la partie "le référentiel galiléen du laboratoire" signifie seulement qu'on néglige de tenir compte du mouvement du laboratoire entrainé par la rotation de la Terre, par la rotation de la Terre autour du soleil, du mouvement du soleil dans la Galaxie, etc.
Maintenant, il ne faut pas confondre la rigueur mathématique et les calculs en physique. Cependant, le physicien compétent précise ses hypothèses physiques, et explicite ce qu'il néglige. Ici, il n'est pas dit que g est négligé.

Ici, faute de connaître la signification de et de je ne sais pas quelle équation est correcte, seulement que la deuxième ne se déduit pas de la précédente.

Cordialement

[tin123tin]

z est l'axe vertical qui nous permet d'étudier la position de M, donc dans les équations z est définit comme la position de M par raport à l'origine c'est à dire la longueur du ressort de son point d'accroche au plafond jusqu'à M.

L0 est la tension à vide du ressort.

[gg0]

Heu ... n'est pas plutôt la valeur de z à l'équilibre ? Dans ce cas, c'est la première équation qui est fausse. Elle est d'ailleurs écrite bizarrement avec ce +mg au début, qui devrait s'éliminer avec la tension à l'équilibre du ressort.

[invite18230371]

Comme écrit le l0 est plutot la longueur à vide du ressort.
Sinon oui je n'ai pas vu que g disparaissait dans l'équation du corrigé. Bien vu.

Mon commentaire sur le "supposé" galiléen c'est simplement pour se rappeler qu'il ne l'est pas en toute rigueur. (pendule de foucault, ect...)
Mais que dans le cadre d'une description de cette expérience, on va le considèrer ainsi.

Ma prof insisté beaucoup pour qu'on écrive à chaque fois cette petite phrase avant d'appliquer le PFD.

[gg0]

Je ne pense pas que ce soit la longueur à vide, dans l'équation finale, c'est bien la position d'équilibre (la valeur de z s'il n'y a pas d'oscillation) du ressort avec la masse m suspendue.

[invite18230371]

mg-k(z-l0)=m (z̈)

On y reconnait le poids +mg
Et la force de rappel du ressort -k.(z-l0)

la longueur à l'équilibre est donc:
mg = k.(le-l0)
le = mg/k+lo

[gg0]

Effectivement.

mais comme les deux équations sont contradictoires, on peut y trouver ce qu'on veut. On dirait que l'auteur a pris deux bouquins différents, qui traitent le problème avec des hypothèses différentes, et copié une équation dans l'un et l'autre dans l'autre ...

Cordialement.

[albanxiii]

Bonjour,

Dois-je comprendre que le "g" est négligeable car nous sommes dans le référentiel galiléens mais que par un souci de rigueur il est préférable de l'intégrer à l'équation ?

Non, absolument pas.
Et quand on néglige un terme dans une équation, on doit le justifier explicitement.

Vous vous rendrez compte dans quelques mois que tout ce que vous faites ici est plutôt inutile, car cela ne vous avancera pas plus une fois l'année scolaire commencée. Je vous conseille de plutôt profiter des derniers jours qui vous restent avant la rentrée pour faire des activités qui vous plaisent, hors champ scolaire.