suite

[adnane045]

bonjour
est ce que une suite peut avoir seulement un element ?
merci
-----

[gg0]

Une suite finie, oui. mais ça n'a pas trop d'intérêt.
A moins que tu veuilles dire que les termes d'une suite (donc infinie) soient tous les mêmes. Dans ce cas on parle de suite constante.

Codialement.

[adnane045]

merci beaucoup pour votre reponse
mais dans ce cas pourquoi ceci est vrai tel que l intresection peut avoir au moins seulement un element ?
si xn est une suite peut avoir 2 elements donc ceci ne sera pas vrai ?

cordinalement

[adnane045]

bonjour

pourquoi ceci est vrai tel que l intresection peut avoir au moins seulement un element ?
si xn est une suite peut avoir 2 elements donc ceci ne sera pas vrai ?
Screenshot 2022-01-07 213641.png
cordinalement ,

Screenshot d01-07 221437.png

[A voir en vidéo sur Futura]

[amineyasmine]

bonjour
est ce que une suite peut avoir seulement un element ?
merci

Oui
Soit l’ensemble des suites suivantes :
On prend un triangle quelconque T1 comme premier élément d’une suite.
On prend le plus petit côté et on extrait de T1 le triangle isocèle associé à ce petit coté et on obtient un nouveau triangle T2

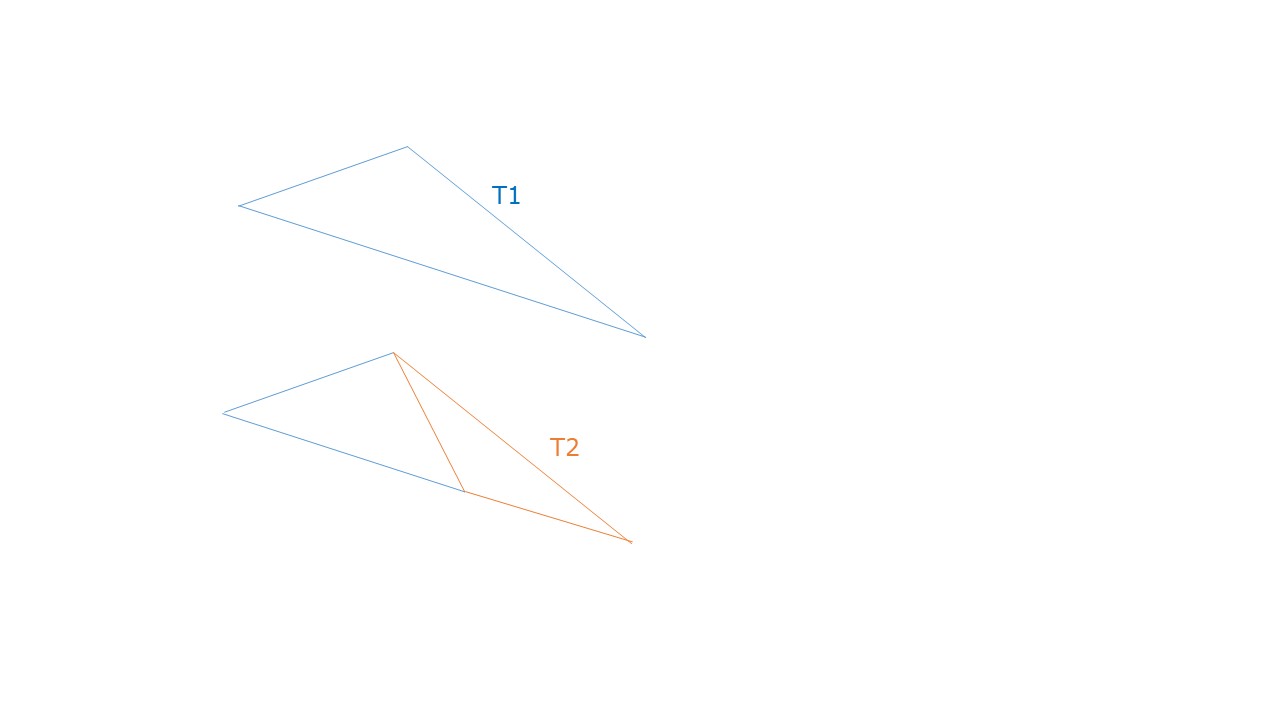
Et on continue ainsi de suite
Si T1 est un triangle équilatéral, il sera le seul élément de la suite, tu peux le vérifier

[adnane045]

mercii
tu peux m expliquer pourquoi on a choisi qu il existe une suite apparient a l'intersection et pas seulement un element ?

[jacknicklaus]

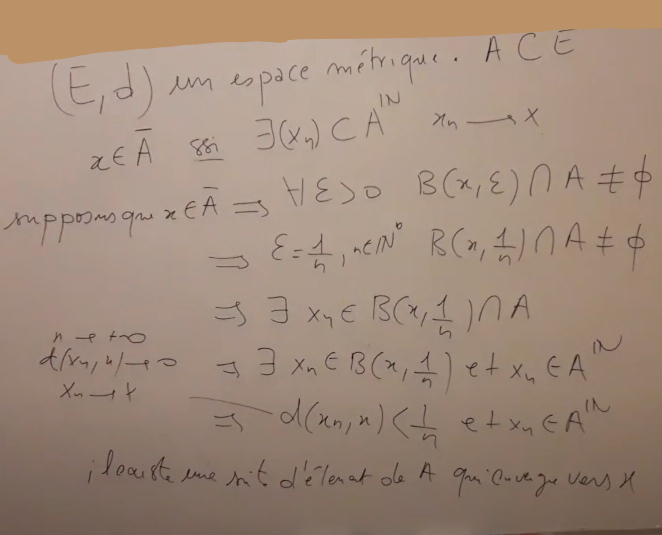
Bonjour

mais dans ce cas pourquoi ceci est vrai tel que l intresection peut avoir au moins seulement un element ?
si xn est une suite peut avoir 2 elements donc ceci ne sera pas vrai ?
cordinalement

On ne sait pas qui est A alors difficile de répondre. Mais à ce qu'on voit, il n'y a aucune raison de penser que xn soit unique. Tout ce qui est écrit, c'est que pour tout entier n, il existe (au moins) un élément nommé xn, à la fois dans A et dans la boule B(x,1/n).

Pourquoi parles tu de suite ? Existe t-il d'autres éléments de contexte que tu n'as pas communiqué ?

EDIT
ceci est une réponse au message #3

[gg0]

Bonjour.

Tu aurais dû ne faire qu'une seule discussion, puisque c'est le même problème que ta discussion suites. Les éléments d'une suite n'ont à priori aucune raison d'être différents. Dans ce sens, une suite peut "n'avoir qu'un seul élément" (on dit plutôt "une seule valeur").
C'est le cas de ta preuve pour l'espace ultramétrique défini sur un ensemble E non vide (*) défini par la distance :
* si , alors d(x,y) =0
* si , alors d(x,y)=1
Je te laisse prouver que d est bien une distance (un exercice de base sur les métriques) et que pour , la boule ouverte de centre x et de rayon r est {x}. En appliquant la preuve avec A={x} où x est un élément de E, tu obtiens la suite (x,x,x,x, ...) suite constante, de seule valeur x, et qui évidemment converge vers ... x.

Cordialement.

(*) j'ai besoin qu'il soit non vide pour ma démonstration

[gg0]

Ce message doublonne avec suite.
Adnane045, les doublons sont interdits !!

[gg0]

Adnane45,

tu devrais revoir ce que signifie le mot "suite". Tu te crée des problèmes inutiles avec une notion simple !! 1,1,1,1,1,1,1,.... est une suite composée avec un élément de R.

[JPL]

J’ai fusionné les deux discussions, mais je laisse un modérateur plus qualifié décider du ménage à faire éventuellement dans ce sujet.

[MOHAMED_AIT_LH]

@ Adnane45: Ta seconde question est en relation avec l'axiome du choix(juste pour information, sinon, tu n'as pas besoin d'approfondir les choses là dessus, il suffit de comprendre ce qui ce passe): Pour tout entier naturel non nul , on a

donc l'ensemble

contient au moins un élément; il peut en contenir plus qu'un mais puisqu'il est non vide, on se permet d'en choisir un qu'on note. Avec le changement de , l'élément peut changer ou pas, mais cela ne pose pas de problème car de toute façon on dispose de , pour tout et qui vérifie la condition

ce qui donne naissance à la suite tel que la condition est réalisée, laquelle favorise, en particulier, la convergence de la suite vers .