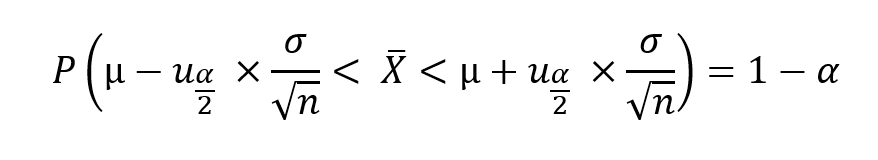Statistique : bornes intervalle

[leroisinge]

Bonjour à tous,

J'ai du mal avec cette question de mon exercice. Elle s'appuie sur les TD, mais je crois que nous n'en sommes pas encore arrivés là en TD encore.

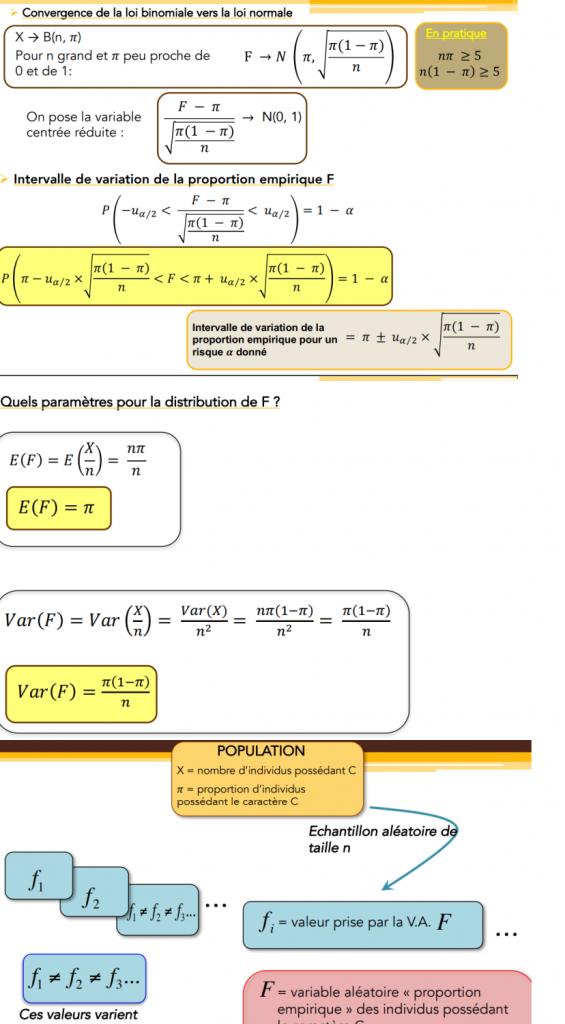
En TD, jusqu'à maintenant, nous avons appris à calculer des probas avec la loi normale. Concernant les intervalles, devions calculer des bornes intervalles de fluctuations avec un risque alpha donné.

Aussi, c'est la question et la ... "mise en page" qui me perturbe. Au début de l'énoncé indique qu'à chaque fois qu’un risque alpha devra être pris en compte, celui-ci prendra la valeur de 5%.
(à la première question, nous calculons les probabilités de vitesse de croissance de l'algue grâce à une loi normale)

Pouvez vous me donner un coup de pouce s'il vous plait ?
Merci !

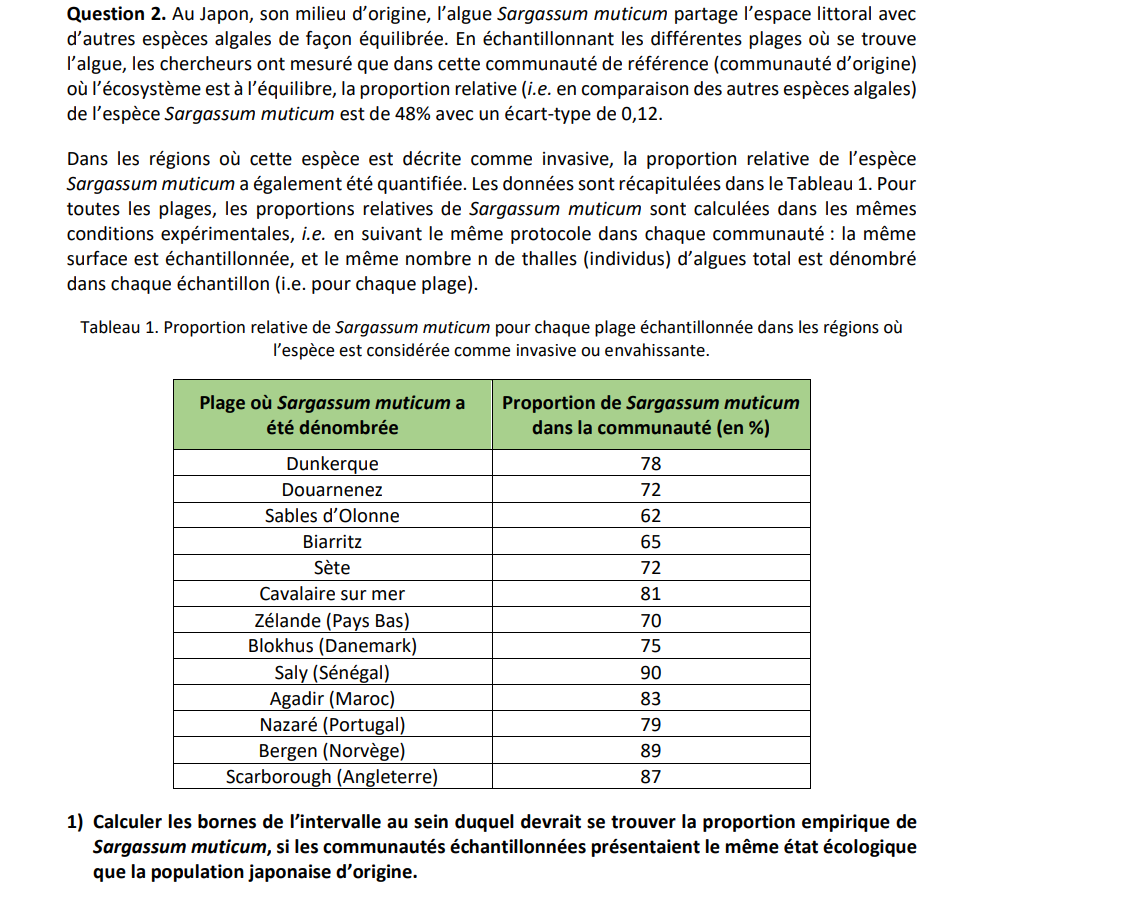
1 PJ :

-----

[gg0]

Bonjour.

Difficile de t'aider sans savoir ce que tu as vu en cours sur les intervalles de fluctuation pour des pourcentages. S'il n'y a rien, tu peux appliquer la méthode habituelle avec la loi Normale, c'est un peu limite, mais pas incohérent.

Cordialement.

[leroisinge]

Bonjour,
Merci de votre réponse gg0.

Pouvons nous reformuler la question de l'énoncé s'il vous plait ?

On m'a conseillé de me baser sur les diapos en PJ, mais je ne comprends pas pourquoi...enfin, c'est la première fois que j'applique ces formules.

1 PJ :

[gg0]

Ces diapos, c'est ton cours ?

N'importe comment, pour le modèle (communauté de référence), tu n'as pas l'effectif d'un tirage dans la population (n), et il est même possible que les 48% et 0,12=12% soient des résultats consolidés de nombreuses enquêtes. Donc la méthode d'estimation à partir d'un échantillon représentatif ne sert à rien ici.

Encore une fois, qu'y a-t-il dans ton cours de stats ?

[A voir en vidéo sur Futura]

[leroisinge]

N'importe comment, pour le modèle (communauté de référence), tu n'as pas l'effectif d'un tirage dans la population (n), et il est même possible que les 48% et 0,12=12% soient des résultats consolidés de nombreuses enquêtes. Donc la méthode d'estimation à partir d'un échantillon représentatif ne sert à rien ici.

Ah ! je me disais bien que c'était bizarre, et que ca ne collait pas à l'énoncé !
Oui c'est mes diapos de cours

Encore une fois, qu'y a-t-il dans ton cours de stats ?

- Tout le chapitre 1 porte sur la loi Normale : loi normale centrée réduite, calcul de proba, approximation de la loi binomiale par la loi normale...
- Le chapitre 2 porte sur l'échantillonnage et estimation : théorème central limite, notion de population et d'échantillon, l'intervalle de variation (fluctuation) d'une moyenne empirique pour un risque alpha donné, intervalle de
variation d’une proportion, théorie de l'estimation, estimation par intervalle de confiance de µe estimation par intervalle de confiance d’une proportion π, intervalle de confiance
- Le chapitre 3 porte sur les tests d'hypothèses
- Le chapitre 4 porte sur les tests de Chi²

Je vous joins le diaporama du cours 2 en message privé si jamais vous souhaitiez y jeter un coup d'oeil.

(je dois avouer que nous avons quelques difficultés à partir du chapitre 2, car c'est assez nouveau, et car aussi les étudiants bavardent beaucoup ce qui gène la compréhension du cours.

[gg0]

OK.

Tu as le cours classique, donc rien sur les intervalles de dispersion d'une proportion.Il arrive que ça pose des problèmes d'utiliser le modèle gaussien sur une proportion, mais ici, on voit que l'intervalle de 4sigma autour de la moyenne va de 0 à 96%, et il contient quasiment tous les cas de valeurs d'une loi Normale (je soupçonne que le 0,12 a été choisi pour ça). Donc utiliser la modélisation par une loi Normale est très raisonnable, et tu retombes sur la méthode déjà utilisée.

Si tu as des problèmes de compréhension (*), n'hésite pas à poser tes questions dans la suite du fil de discussion.

Cordialement.

(*) il peut y en avoir beaucoup, car décider de ce qui est aléatoire et ce qui ne l'est pas est délicat.

[leroisinge]

Si tu as des problèmes de compréhension (*), n'hésite pas à poser tes questions dans la suite du fil de discussion.

Merci beaucoup !

Comment dois je procéder avec une loi normale ? Je ne vois pas quelle "procédure" je pourrais suivre.
Après avoir relu l'énoncé plusieurs fois, j'aurais tendance à vouloir calculer les bornes de intervalle avec un risque alpha. Est ce que c'est cela ?
Comme je l'ai dit plus haut, le risque alpha à prendre en compte est de 5%

J'ai l'impression que c'est la seule question qui nécessite de prendre en compte un risque alpha, et que les autres questions portent sur les tests d'hypothèses. Je peux vous joindre les exercices ou les questions en message privé si nécessaire.
C'est difficile de se projeter car nous n'avons pas fait tous les TD encore...

Cordialement

[gg0]

Effectivement, tu vas calculer un intervalle de dispersion à 95% de la moyenne, ce qui nécessite la taille des échantillons. Il y a ici un réel problème, cette taille n n'est pas donnée !! Ce qui fait qu'à priori, on ne peut pas répondre à la question.
On est donc ramené au modèle gaussien, pour lequel il y a 95% de chances qu'une moyenne soit entre 0,48-1,96*0,12 et 0,48-1,96*0,12.
C'est peut-être à ça que pensait l'auteur du sujet.

Cordialement.

NB : A priori, je traite les questions sur le forum. D'autres aussi y répondent.

[leroisinge]

Pardon de ma réponse tardive !

Je pense que nous sommes sur la bonne piste. J'ai parlé à ma professeure avant de lire votre réponse. Elle m'a expliqué que cet exercice faisait appel au TD 1 (lois normales etc...) et le TD 2 (qui se base sur le chapitre 2 : calcul d'intervalle de confiance, de fluctuation etc...)

Oui, je suis surpris de voir que je n'ai pas la taille des échantillons, comment procéder ?

On est donc ramené au modèle gaussien, pour lequel il y a 95% de chances qu'une moyenne soit entre 0,48-1,96*0,12 et 0,48-1,96*0,12.

Je fais essayer de poser le calcul, et voir si je trouve cela. Je vous tiens au courant !

(vouliez vous dire "0,48-1,96*0,12 et 0,48-1,96*0,12" ?

NB : A priori, je traite les questions sur le forum. D'autres aussi y répondent.

Oui ! je sais, il faut que ce soit profitable aux autres également.

[leroisinge]

Je voudrais compléter mon précédent message ci dessus : comment procédez vous sans connaitre n ?

[gg0]

n n'intervient pas, puisqu'on demande un intervalle de dispersion (fluctuation) sur une seule variable gaussienne (la proportion empirique attendue si ..). Et tu as tout ce qu'il te faut sur cette variable gaussienne.

Cordialement.

[leroisinge]

Je ne sais pas si je fais une confusion : en classe, nous avons vu cette formule pour calculer l'intervalle de fluctuation de la moyenne empirique.
Nous avons aussi vu l'intervalle de confiance de la variable aléatoire.

Pour calculer l'intervalle de fluctuation d'une VA gaussienne, est ce que cela se base sur la même méthode que ce que je viens d'évoquer ?

[gg0]

Ça c'est pour une moyenne, mais ça se base sur l'intervalle centré pour une variable gaussienne. Tu es capable de déterminer un intervalle à 95% pour une variable Normale, l'intervalle centré tel que 95% des réalisations sont dedans.
Revois ton premier chapitre, les modélisations par des lois Normales sont à la base de nombreuses questions.

Cordialement.

[leroisinge]

Oh ouiiiii ca me dit quelque chose !
Oui !
J'ai compris là où vous voulez en venir !

Merci beaucoup ! Je retenterai ca dès ce soir, je vous tiens au courant !

Cordialement

[leroisinge]

Bonjour gg0

Voici mon travail !
Je pense que la première partie de démonstration n'est pas nécessaire. Cependant, la professeure nous avait dit de ne pas retenir la formule, mais qu'on pourrait la retrouver si besoin.
Je suis assez content d'avoir réussi...mais je ne sais pas si j'ai bien justifié : l'énoncé de cette question ne mentionne pas que la variable aléatoire suit une loi normale.

Qu'en pensez vous ?

Cordialement

1PJ :

[gg0]

Pourquoi n'as-tu pas écrit l'intervalle ? Tu sais faire des additions et soustractions. Et tu en auras besoin pour la suite.
D'ailleurs, le 0,48 étant probablement un arrondi, le 0,2352 est trop précis; par précaution on prendra (en le disant, plutôt 0,24, qui ne réduit pas l'intervalle.
Enfin tout ce calcul aboutit à un classique de la loi Normale : Un intervalle de dispersion à 95% est [m-1,96 s;m+1,96 s] où m est la moyenne, et s l'écart type. En pratique, on remplace souvent 1,96 par 2, et on parle de 4 sigma (intervalle de 4 écarts types).

Cordialement.

[leroisinge]

Pourquoi n'as-tu pas écrit l'intervalle ?

Oh ! J'avais imité la rédaction notre façon de faire en TD.
Je vais changer ma rédaction alors : pour un risque alpa = 5%, X appartient à l'intervalle [0.24; 0,7] (en arrondissant le 0.2352 à 0.24)

Oh, je ne savais pas pour le 4 sigma, merci ! Je note !

Et tu en auras besoin pour la suite

Puis je solliciter votre aide s'il vous plait pour la question suivante, sur ce même énoncé ?

Il m'est demandé "Quelle(s) conclusion(s) pouvez-vous formuler quant aux populations de Sargassum muticum échantillonnées en-dehors du Japon ?"
A quoi dois je m'intéresser ?
Dois je dire si ces populations font, ou non, parti de l'intervalle de fluctuation à 95% ?

[leroisinge]

(J'avais imité la rédaction de notre TD) *

petite faute de frappe dans mon précédent message !

[gg0]

Regarde les valeurs dans le tableau et conclus toi-même. Bien évidemment, en utilisant ce que tu as trouvé à la question précédente.
NB : 0,48+0,24 = 0,72, pas 0,7.
Alors, que vois-tu ?

[leroisinge]

NB : 0,48+0,24 = 0,72, pas 0,7.

Pardon, et merci !

Alors, que vois-tu ?

Je vois qu'à Douarnenez, aux Sables d'Olonne, à Biarritz, en Sète et à Zélande (aux Pays Bas) : la proportion relative fait partie de l'intervalle de confiance dans lequel doit se trouver 95%de proportion empirique de Sargassum muticum. Elle peut être considéré comme non envahissante dans ces zones là
A Dunkerque, Cavalaire sur mer, Blokhus, Saly, Agadir, Nazaré, Bergen, Scarboorough, la proportion d'algues est supérieure à la borne supérieure de l'intervalle de confiance. On en déduit qu'elle est beaucoup invasive que la normale.

Est ce cela ?

[gg0]

Oui, c'est une interprétation possible, bien que le fait que 0,72 soit dans l'intervalle de dispersion soit douteux.
Mais un regard global montre que toutes les valeurs sont au dessus de la moyenne japonaise. C'est interprétable soit par l'idée que toutes ces stations sont plus envahies, soit par l'idée que les statistiques japonaises sont très particulières.
D'autres idées sont possibles.

Cordialement.

[leroisinge]

Merci beaucoup gg0 !

C'est compris !

A bientot sur le forum,
Cordialement

[leroisinge]

Bonjour gg0, je me posais des questions sur cet exercice.

Je cherche à l'expliquer à mes camarades qui n'ont pas compris. Cependant, je ne sais pas répondre à leur questions :

- Comment puis je affirmer que la proportion des algues suit une loi normale ?
- Dans ma méthode, j'ai utilisé µ=0.48. Or, mes camarades ne comprennent pas le raisonnement, puisque l'énoncé indiquent que la proportion d'algues au Japon =0.48
- Ils pensent que nous pouvons accéder au n, en comptant le nombre le plage où l'algue a été dénombrée.

En fait, j'ai compris la méthode que nous avons suivie, je saurais expliquer comment j'ai procédé, mais pas pourquoi.

[gg0]

Bonjour.

"- Comment puis je affirmer que la proportion des algues suit une loi normale ?" Ce n'est qu'une hypothèse de travail. Faute de renseignements sérieux, on ne peut qu'espérer que cette proportion a été calculée sur un grand nombre de thalles, et donc que l'approximation de la binomiale par une gaussienne peut se faire. Sinon, le 0,48 n'a aucun intérêt.

"- Dans ma méthode, j'ai utilisé µ=0.48. Or, mes camarades ne comprennent pas le raisonnement, puisque l'énoncé indiquent que la proportion d'algues au Japon =0.48" Ce n'est pas une proportion, mais une proportion moyenne, sinon le "avec un écart type de 0,12" n'a aucun sens. Le texte est assez flou, il faut l'interpréter.

"- Ils pensent que nous pouvons accéder au n, en comptant le nombre le plage où l'algue a été dénombrée." On ne parle pas ici de la moyenne des différentes plages, mais d'étudier différentes proportions. Que dire de 78% à Dunkerque, résultat d'une division d'un certain nombre d'algues particulières sur un certain nombre total d'algues ? Et on ne sait rien sur ces "certains nombres".

La démarche que j'ai proposée est critiquable (choix d'une hypothèse), mais je n'en vois pas d'autres. Et c'est malheureusement souvent le cas en stats.

Cordialement.

[leroisinge]

Merci gg0 !

C'est clair !
Je suis d'accord avec vous, et la méthode utilisé. Et je ne suis donc pas d'accord avec celle de mes camarades.
La votre me parait plus logique. La leur est tirée par les cheveux.

Merci de votre temps !

[gg0]

"La leur est tirée par les cheveux." je ne sais pas, je ne l'ai pas vue exposée complétement. Mais il leur faut dire quelle variable statistique est utilisée et quel résultat du cours l'est.