Intégrale de Gauss - Encadrement par intégrale de Wallis

[5t3ph]

Bonsoir à tous,

je bute sur la dernière étape du calcul de l'intégrale de Gauss par encadrement.

Jusque là, tout va bien :

futura1.png

C'est cette implication qui me pose problème :

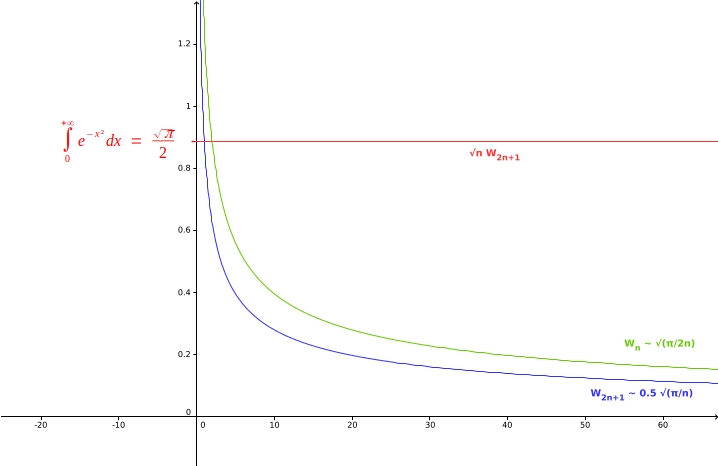
futura2.png

Je ne comprends pas pourquoi W(2n+1) & W(2n-2) ne sont pas équivalents à W(n) lorsque n tend vers l'infini.

Merci par avance !futura2.pngfutura1.png
-----

[5t3ph]

Désolé, je galère avec les pièces jointes, je tente de rectifier

[gg0]

Bonjour.

Remplace n par 2n dans la formule de Wn.

Cordialement.

[5t3ph]

Mais quel ***
J'ai presque honte là, j'avais réussi à faire le plus dur

Merci !

[A voir en vidéo sur Futura]

[gg0]

Mais c'est au contraire à moi de te remercier : je n'avais jamais réalisé que U(2n) n'a aucune raison d'être équivalent à U(n).

Cordialement.

[5t3ph]

> U(2n) n'a aucune raison d'être équivalent à U(n)
Oui... Je me suis un peu emmêlé les pinceaux. En me disant que puisque U(2n) est une suite extraite de U(n) qui converge, elle converge vers la même limite. Et que donc son équivalent devait être le même. Ce qui est faux bien entendu.

Tout est okay maintenant

Et quand je trace les courbes des différents équivalents, je tombe bien sur la valeur approchée de l'intégrale de Gauss entre 0 et +inf (0,886...)