Fit d'une série de donnée de température

[cirrus007]

Bonjour à tous,

Peut-être que ma question pourra sembler simpliste, ou du moins plutôt orientée vers un niveau "lycée" vu la difficulté des exercices que j'ai pu voir à droite à gauche sur cette section ^^ Mais bon je tente par ici, je n'ai pas trouvé de solution si évidente, voici mon problème.
Je dispose de série de mesure de température au cours du temps issues d'un datalogger. Pour contextualiser il s'agit de système d'incubation pour microscope que nous mesurons, ceux-ci partent de la température de la pièce (souvent autour de 20°C) jusqu'à atteindre une consigne de 37°C, ces systèmes sont utilisés en sciences du vivant pour imager par microscope des organismes vivants (cellules, embryons etc). Enfin bref je ne rentre pas dans le détail biologique des choses
En l'occurrence donc, je dispose de fichier .txt, avec une mesure de température toutes les 30sec, sur une période de temps de mesure variant entre 60min à 180min la plupart du temps.

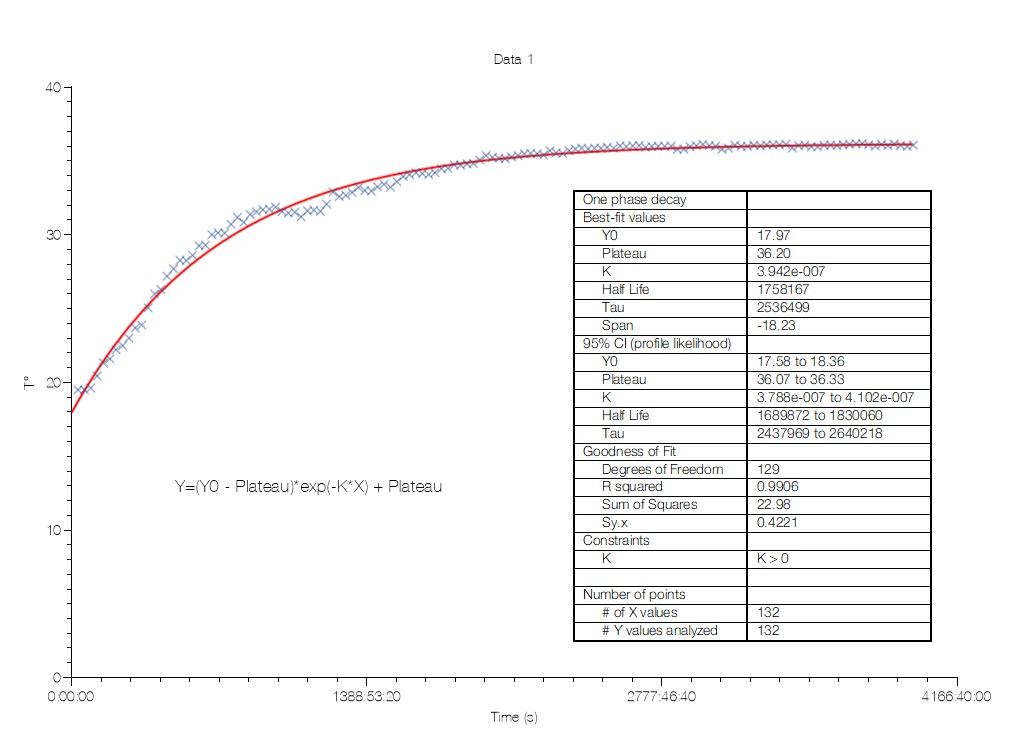
Voici le type de courbe que l'on obtient régulièrement:

Capture.PNG

L'idée derrière est déterminer de façon mathématique le temps nécessaire à la stabilisation, c'est à dire à partir de quand la température ne varie plus significativement. Conceptuellement et à vue d'œil c'est quelque chose assez simple à trouver, sur l'exemple du dessus par exemple on peut se dire qu'à partir de 3000sec la température est stable. Mais j'aurai aimé trouver une méthode mathématique fiable et reproductible pour tomber sur cette valeur.
J'ai essayé différentes solution, que je vais vous exposer ici, mais aucune n'est "facile et directe" dans l'interprétation des résultats:

1- Méthode de dérivée 1ère:
Intuitivement je me suis dis que la dérivée première de cette courbe de mesure pourrait solutionner les choses, en effet dans ma tête une dérivée qui passe par zéro signifie une absence de variation (et/ou changement de signe d'une fonction), ainsi plus la dérivée s'approche et reste colée à zéro, cela signifie qu'il n'y a plus de variations.
en faisant tout betement ce type de calcul sur ma feuille Excel:
Capture2.PNG

Et en traçant le graphique correspondant je trouve ceci (la courbe bleue)

Capture3.PNG

La mesure de dérivée est un peu "bruitée" (je ne sais pas si c'est le bon terme?), du coup j'ai fait un petit coup de moyenne mobile 4 période, les pointillés en orange. Et ainsi j'ai déterminé que si il n'y a plus de dépassement de la dérivée première au dessus de 0.2°C/min durant au moins 1000sec consécutive (>15min), alors le système est dit "stabilisé en température". Mais.... malheureusement ce critère ne fonctionne pas avec toutes les courbes de températures, certaines sont un peu moins "faciles" et ce critère ne tient pas la route, voici l'exemple de courbe de température qui m'a causé problème:

Capture4.jpg

Du coup problème... mais j'avais une seconde idée en tête:

2- Fit polynomial sous Excel
Les courbes que je vous présentent me font penser à des fonctions polynomiales, je me suis donc dit qu'avec Excel j'arriverait sans problème à les fitter, générer l'équation de la courbe et la dériver derrière pour trouver les racines du polynomes... oui sauf que ... très souvent les courbes ne fittent pas avec un polynome d'ordre 2 ou 3, il faut augmenter la complexité du polynome à un degré 5 ou 6 (le maximum possible sous Excel), et cela devient bien plus complexe à dériver, trouver les racines du polynomes etc... j'ai essayé avec différents sites en lignes (Desmos en particulier), mais ça reste du bricolage et on est loin d'une solution efficace.

Voici par exemple un fit sous Excel efficace... mais polynome 6!! (donc dérivée polynome 5=> un enfer pour trouver simplement les racines du polynome).

Capture5.PNG

En somme je pense que cette méthode de fit polynomial est extremement puissante, MAIS je n'ai pas les outils analytiques derrières sous Excel...
Peut-être qu'avec R cela se fait facilement? Ou Matlab? Un truc open-source serait l'idéal, je travaille en labo de recherche dans le domaine de la Biologie. J'espère d'ailleurs ne pas avoir fait trop de raccourcis et erreurs dans mes explications, que les puristes en maths m'excusent

Merci pour vos lumières!!
Cordialement,
-----

[albanxiii]

Bonjour,

Votre courbe ressemble fortement à une exponentielle. Si vous tracez son logarithme en fonction du temps et que ça fit avec une droite vous pouvez remonter aux paramètres.

[cirrus007]

J'oubliais, si besoin, voici un exemple de set de données sous Excel

exemple T data.xlsx

[Flyingbike]

Bonjour,

Votre courbe ressemble fortement à une exponentielle. Si vous tracez son logarithme en fonction du temps et que ça fit avec une droite vous pouvez remonter aux paramètres.

je dirais même plus, voici le fit que j'obtiens sous Prism, c'est assez propre (et de toute façon, physiquement, c'est comme cela que c'est décrit)




Ca devrait aller pour le modèle, ensuite pour en tirer le temps qui vous intéresse, il faut par exemple se définir une tolérance par rapport au "plateau" et voir le temps mis pour atteindre cette valeur en prenant en compte une moyenne glissante sur n points.

[A voir en vidéo sur Futura]

[albanxiii]

C'est plus impressionnant qu'une droite !
De mon temps on savait rien fitter les droites à la main, le reste c'était plus difficile

[JJacquelin]

Bonjour

Avec le modèle d'équation suivant :

Result Fitting exp.GIF

NOTE :

Habituellement l'ajustement des paramètres a, b, c se fait par une méthode de régression non linéaire. Les logiciels usuels utilisent des algorithmes de calcul itératifs qui nécessitent de donner au départ des valeurs approchées ( supposées ou estimées) aux paramètres ou, au moins, une plage pour chacune de ces valeurs. Ceci n'est pas toujours facile. Des valeurs initiales trop éloignées des valeurs correctes sont fréquemment la cause de non convergence du calcul itératif et parfois même d'erreur grossière de résultat.

Pourtant il existe une méthode (peu connue) de calcul non itératif qui ne nécessite pas de donner des valeurs initiales. Les valeurs de a, b, c données sur la figure ci-dessus ont été calculées grâce à cette méthode. Le schéma du calcul non itératif est joint ci-dessous, avec le détail (très simple) du calcul numérique.

Algo Ajust Exp.GIF

Calcul Ajust Exp.GIF

Pour information sur le principe de cette méthode : https://fr.scribd.com/doc/14674814/R...ons-integrales

[cirrus007]

Je réponds un peu tardivement, mais milles merci pour vos réponses car c'est vraiment le type d'équation sous forme d'exponentielles qui correspond bien !
Je suis parti de l'équation proposé par FlyingBike, sous la forme y= (a-b)*exp(-c*x)+b, j'utilise un logiciel d'analyse d'image assez répandu dans la communauté scientifique qui s'appelle Fiji (alias ImageJ) qui dispose d'une fonction "curve fitter" assez efficace et j'obtiens ainsi les paramètres a,b et c. C'est propre et efficace, rien à dire la qualité du fitting est souvent entre 0.999 et 0.95 en fonction des datas que je met en input et j'extrais très simplement les paramètres a,b et c.

Pour cette notion de stabilité, c'est maintenant là où j'aurai besoin de vos lumières et j'aimerai aussi rebondir sur le propos de FlyingBike "ensuite pour en tirer le temps qui vous intéresse, il faut par exemple se définir une tolérance par rapport au "plateau" et voir le temps mis pour atteindre cette valeur en prenant en compte une moyenne glissante sur n points."

La question de la tolérance est vraiment la clé du problème j'ai l'impression, je vous fais part de mon cheminement de pensée avec mes mots et mes faibles connaissances mathématiques (disons niveau Terminale S maintenant, les maths remontent à trop loin pour moi maintenant malgré mon Master en biologie haha).

J'ai d'abord naïvement cherché à dériver cette fonction y= (a-b)*exp(-c*x)+b, je tombe sur une fonction y'= c(b-a)*exp(-c*x), mon idée initiale était de trouver y'=0 afin de trouver la stabilité et le plateau, sauf que y' ne peux pas prendre de valeur en zéro étant donné que ni c(b-a) ni exp(-c*x) ne peuvent valoir zéro, si je ne dis pas de bêtise cette fonction est asymptotique à la valeur b en +l'infini, donc pas possible de raisonner avec une dérivée qui vaut zéro pour trouver la stabilité.

D'ailleurs même résultat si je veux lire la valeur en x de la fonction y; ainsi pour y=b, je trouve: x=-ln ((y-b)/(a-b)/c) ; et bien entendu si y=b on tombe sur un magnifique ln(0) qui ne m'aide guère plus.

J'ai donc cherché une autre façon, en cherchant à approcher cette notion de "tolérance au plateau" abordée par FlyingBike, j'ai remplacé la valeur y par (b-0.2), de façon totalement empirique en me disant que cette valeur de 0.2°C correspondait plus ou moins à la précision réelle du thermomètre de mesure, en procédant ainsi je tombe sur des valeurs de stabilisation plutôt cohérente (par exemple pour le cas de figure que je vous ai donné, je tombe sur X= 3179sec, ça me semble plutôt cohérent à l'œil). Mais je reste un peu chiffonné par le fait que j'ai mis cette valeur un peu "au feeling", sans gros argument mathématique derrière pour le justifier.
L'idée de valeur glissante sur n points me semble intéressante, faudrait-il faire cette moyenne glissante à partir de la courbe fittée ou bien à partir des données expérimentales ? Etant donné que je dispose de nombreuses séries de données, j'imagine qu'il va falloir que je fasse cette moyenne glissante sur toutes mes courbes, et faire une sorte de moyenne à la fin afin d'extraire ma vraie tolérance ...

Qu'en pensez-vous ?
Merci encore

[MissJenny]

2- Fit polynomial sous Excel

un polynôme ne convient pas pour modéliser une courbe qui a une asymptote horizontale. On montre facilement que les polynômes tendent vers + ou - l'infini quand la variable tend vers l'infini. Là tu pourrais essayer une fonction comme a*(1-exp(-bt)) avec des paramètres a et b à estimer.

et au fait, en français fit se dit ajustement.