Bonjour est-ce que l'on peut trouver le polynome de degré 2 avec une suite finie de termes ?
J'ai des suites qui sont construites avec des termes calculés par la formule
par exemple avec les fractions suivantes :
87381/1
145635/5
184471/19
35599/11
460639/427
219711/611
233855/1951
418047/10463
366079/27487
156671/35291
366591/247729
331775/ 672605
483327/2939533
409599/7473389
360447/19729747
327679/53808401
131071/64570081
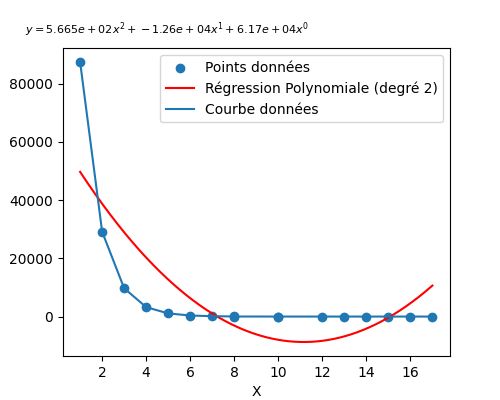
J'obtiens la parabole suivante qui ne passe pas sous l'axe des abscisses et je cherche comment calculer l'équation polynomiale de la courbe de tendance donnée par le tableur pour chercher ensuite les solutions (de ce que j'ai pu lire il faut passer par le plan complexe pour ces polynomes) :
-----