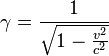Variabilité de la masse-énergétique du photon

[invite9438e0bf]

Bonjour,

je me pose une question concernant la lumière.

J'ai cru comprendre en lisant divers choses, que le photon, grain de lumière, serait une particule de masse nulle au repos.

J'ai compris également que cette particule est plus ou moins énergétique (selon sa longueur d'onde Lamba) : des rayons gammas sont plus énergétiques que la lumière visible http://fr.wikipedia.org/wiki/Photon.

Donc, le photon peut "contenir" différentes énergies. Et on sait par ailleur via l'équivalence masse-énergie que plus une particule est énergétique, plus elle est "massive" en terme d'énergie, et inversement.

J'en viens donc à mes questions sur la dite masse du photon :

1°) la masse du photon est-elle augmenté par son énergie ?

2°) si on ralenti le photon, sa masse diminue-t-elle ?

3°) la masse-énergie est-elle identique à la masse des particules communes ? càd : est-elle soumise aux mêmes loi de la gravitation : plus on est lourd, plus l'attraction est grande (selon ) ?

4°) Suite à cela, peut-on affirmer que les photons sont plus ou moins déviés par un même corps stellaire, selon leur longueur d'onde (diffusion du spectre par effet gravitationnel) ?
-----

[invite88ef51f0]

Salut,

Et on sait par ailleur via l'équivalence masse-énergie que plus une particule est énergétique, plus elle est "massive" en terme d'énergie, et inversement.

Non. La relation E=mc² ne te donne que l'énergie au repos (on devrait écrire E₀). L'équation complète est E²-p²c²=m²c⁴. Pour un photon, on a m=0 et donc E=pc.

Il me semble que c'est bien expliqué dans la FAQ de la rubrique "Physique".

Ensuite, tu ne peux pas appliquer les lois de la gravitation newtonienne à des photons. Il faut utiliser la relativité générale qui te dit que l'énergie (et donc la masse) déforme l'espace et que les photons, qui suivent le trajet le plus court, sont donc déviés. Mais cette déviation ne dépend pas de la longueur d'onde.

[invite4baed56c]

Bonjour,
Je me suis souvent posé cette question et j'ai aussi souvent fait fausse route. Il semble que ce ne soit pas sans raison que l'on parle de dualité onde-corpuscule. Il s'avere que la notion de grain de lumière est plus intuitive que réelle, de la même façon qu'un quantum d'énergie E=hv n'est pas à proprement parler un grain d'énergie.

[invite9438e0bf]

Salut,
Non. La relation E=mc² ne te donne que l'énergie au repos (on devrait écrire E₀). L'équation complète est E²-p²c²=m²c⁴. Pour un photon, on a m=0 et donc E=pc.

Il me semble que c'est bien expliqué dans la FAQ de la rubrique "Physique".

Non, ce n'est pas clair dans la FAQ, que j'ai lu avant de poser ma question. Sinon, je ne l'aurais pas posée.

Ensuite, tu ne peux pas appliquer les lois de la gravitation newtonienne à des photons. Il faut utiliser la relativité générale qui te dit que l'énergie (et donc la masse) déforme l'espace et que les photons, qui suivent le trajet le plus court, sont donc déviés. Mais cette déviation ne dépend pas de la longueur d'onde.

Les photons (qui portent de l'énergie) ne déforment-il pas l'espace ?

[A voir en vidéo sur Futura]

[invite88ef51f0]

Non, ce n'est pas clair dans la FAQ, que j'ai lu avant de poser ma question. Sinon, je ne l'aurais pas posée.

Ok. C'est très bien de l'avoir lu. Je t'invite à poser toutes les questions que tu veux dessus et sur mon message ci-dessus qui était très rapide.

Les photons (qui portent de l'énergie) ne déforment-il pas l'espace ?

Si, un peu. Mais c'est négligeable.

[invitec913303f]

Une question que j'aimerais ajouter à ce sujet c'est que si notre photon n'est pas localisé, comment est l'état du champ? probabiliste?

merci
flo

[invite9438e0bf]

Les photons (qui portent de l'énergie) ne déforment-il pas l'espace ?

Si, un peu. Mais c'est négligeable.

1°) Cette petite déformation, si petite soit-t-elle, est-elle proportionnelle à l'énergie-masse du photon ?

2°) En admettant cette petite déformation, et qu'elle soit variable, cela n'influence-t-il pas la trajectoire du dit photon lorsqu'il passe près d'un corps massif (plus ou moins donc selon l'énergie du photon) ?

3°) Question qui se rapporte à la masse et à la vitesse, mais d'un autre point de vue : la masse des particules élémentaire est-elle déduite de leur énergie ou bien de déductions par rapport à une pesée de matière macroscopique ?

4°) Si la masse est déduite de l'énergie, cela se fait dans un accélérateur de particules sans doute. Donc lorsque la particule se déplace à priori lors d'une collision. Mais si on ralenti la particule, son énergie diminue, et sa masse avec ? Alors quelle est la bonne mesure des masses ?

5°) En reparlant du lien énergie-vitesse-masse, j'ai repensé à mes premières questions et je me demandais la même chose avec le photon : quand on le ralenti, perd il de l'énergie-masse ?

Désolé si je vous embête avec toutes mes questions stupides

[invite8c514936]

Salut,

La masse du photon ne peut pas diminuer : elle est nulle. On dit parfois que la masse dimininue quand la vitesse diminue, mais

1/ c'est par un facteur multiplicatif, qui appliqué à une masse nulle continue de donner une masse nulle

2/ ce n'est pas la définition de la masse qu'utilisent les physiciens des particules. La masse est déduite de la relation donnée par Coincoin plus haut.

[invite9438e0bf]

La relation E=mc² ne te donne que l'énergie au repos (on devrait écrire E₀). L'équation complète est E²-p²c²=m²c⁴. Pour un photon, on a m=0 et donc E=pc.

Je reprends donc l'équation, pour avoir la masse :

m²=(E²-p²c²)/c⁴

où E est l'énergie mesurée et p est "l'impulsion" (fonction de la longueur d'onde pour la lumière je crois, je ne sais pas pour les autres particules), également mesurée.

Si c'est comme ça qu'on détermine la masse, comment mesure-t-on ces grandeurs ?

[invite88ef51f0]

Pour une particule massive, et dans les cas simples (sans champ magnétique, ...), l'impulsion est simplement la quantité de mouvement : p=mv.

En physique des particules, pour identifier une particule, si elle est chargée on peut regarder comment elle est courbée dans un champ magnétique (ce qui donne sa vitesse et donc son impulsion), et l'énergie qu'elle libére quand on l'arrête (les détecteurs servant à cette mesure sont appelés des "calorimètres"). Si on a l'énergie et l'impulsion, on a la masse...
On peut aussi regarder la quantité d'énergie perdue par unité de longueur. Pour une énergie donnée, c'est une caractéristique d'une particule.

[invite9438e0bf]

Je reprends donc l'équation, pour avoir la masse :

m²=(E²-p²c²)/c⁴

où E est l'énergie mesurée et p est "l'impulsion" (fonction de la longueur d'onde pour la lumière je crois, je ne sais pas pour les autres particules), également mesurée.

Si c'est comme ça qu'on détermine la masse, comment mesure-t-on ces grandeurs ?

Pour une particule massive, et dans les cas simples (sans champ magnétique, ...), l'impulsion est simplement la quantité de mouvement : p=mv.

En physique des particules, pour identifier une particule, si elle est chargée on peut regarder comment elle est courbée dans un champ magnétique (ce qui donne sa vitesse et donc son impulsion), et l'énergie qu'elle libére quand on l'arrête (les détecteurs servant à cette mesure sont appelés des "calorimètres"). Si on a l'énergie et l'impulsion, on a la masse...
On peut aussi regarder la quantité d'énergie perdue par unité de longueur. Pour une énergie donnée, c'est une caractéristique d'une particule.

Ok alors on a :

E²=m²c⁴+p²c²

soit, comme p=mv, :

E²=m²c⁴+(mv)²c²
E²=m²c⁴+m²v²c²
E²=m² . c² . (c²+v²)

d'où :

m²= E² / (c² . (c²+v²))

Soit donc :

m= E/(c . Racine (c²+v²))

J'espère ne pas me tromper...

Si c'est le cas, au moins j'aurais réussi à comprendre réellement quelque chose

J'ai lu également cette page, qui explique plutôt bien (à rajouter dans la FAQ si c'est bon ?) :

http://fr.wikipedia.org/wiki/E%3Dmc%C2%B2

[invite88ef51f0]

J'ai la flemme de vérifier ton calcul, mais dans l'autre sens, on a :
(au passage, on trouve bien E=mc² pour v=0).

[invite9438e0bf]

Salut,

La masse du photon ne peut pas diminuer : elle est nulle.

Tu parles de m₀ si je ne m'abuse.
Qui vaut bien 0 pour le photon, d'après la théorie (qui semble être improuvable directement, mais bien par l'effet qu'une masse non nulle aurait théoriquement sur le reste de l'univers).

On dit parfois que la masse dimininue quand la vitesse diminue, mais

1/ c'est par un facteur multiplicatif, qui appliqué à une masse nulle continue de donner une masse nulle

Tu parles de l'appliquer à la masse au repos de la particule m₀. Mais quand la particule bouge, la masse réelle n'augmente-t-elle pas avec l'énergie cinétique ?

En fait mon problème de compréhension vient du fait, qu'on peut "convertir" des joules en kilogrammes et inversement, via le facteur c²...
Il est bien dit qu'on ne converti pas une énergie en masse, mais j'ai du mal à saisir la nuance. Car tout ceci semble au final réellement équivalent...

[invite88ef51f0]

En fait, il a deux façons de définir la masse : soit on dit qu'elle varie avec la vitesse, soit on dit qu'elle ne varie pas.
La première façon permet d'élargir plus facilement les résultats de la mécanique classique. La deuxième est beaucoup plus propre et plus rigoureuse.

Je pense qu'ici tu trouveras surtout des partisans de la deuxième définition.

Je t'invite à chercher sur le forum, il y a eu de longs débats sur la question.

[invite9438e0bf]

En fait, il a deux façons de définir la masse : soit on dit qu'elle varie avec la vitesse, soit on dit qu'elle ne varie pas.
La première façon permet d'élargir plus facilement les résultats de la mécanique classique. La deuxième est beaucoup plus propre et plus rigoureuse.

Je pense qu'ici tu trouveras surtout des partisans de la deuxième définition.

Je t'invite à chercher sur le forum, il y a eu de longs débats sur la question.

Donc il s'agit de parler de la bonne masse, soit la masse inertielle (masse au repos), soit la masse-énergie, qui est plutôt l'énergie de la particule converti en unité de masse équivalente (c'est à dire la masse qu'un objet devrait avoir pour contenir la même énergie).

[invité576543]

Donc il s'agit de parler de la bonne masse, soit la masse inertielle (masse au repos), soit la masse-énergie, qui est plutôt l'énergie de la particule converti en unité de masse équivalente (c'est à dire la masse qu'un objet devrait avoir pour contenir la même énergie).

Bonsoir,

Cette notion de "masse-énergie" semble assez impropre. Il n'y a rien de tel. La masse c'est la masse, et l'énergie c'est l'énergie. Il se trouve que dans le référentiel dans lequel un objet de masse non nulle est immobile, son énergie est alors proportionnelle à sa masse, avec un rapport constant pour tous les objets.

Dans d'autres référentiels, l'énergie n'est plus liée à la masse de manière aussi simple, et il faut bien distinguer les deux idées.

En fait mon problème de compréhension vient du fait, qu'on peut "convertir" des joules en kilogrammes et inversement, via le facteur c²...

On peut aussi convertir les mètres et les seconde via le facteur c. Cela te poses-t-il un problème similaire?


Suggestion: ne plus parler de "masse-énergie".

Cordialement,

[invitec913303f]

Bonjour, je souhaiterais réagire humblement à ce sujet lorsque l'on parle de masse au repos ou non. premièrement la masse est un scalaire c'est à dire que c'est une grandeur qui n'à pas de composante dans un repère. (Contrairement à la vitesse qui elle se décris par un vecteur)

En outre, (je souhaite que les spécialistes me donnent leur avi) je "pense" que lorsque l'on parle de m0 et d'augementation de la masse il faut faire attention. En effet, on peut distinguer par exemple temps propre et temps mesuré par un observateur dans un referentiel R'. Pour la masse on peut parler de masse propre à l'exeption que dans un refertiel R' l'observateur pourra dire que tout se passe comme si le bidul en mouvement avais une masse équivalente à ... et ceci en raison de la dilatation du temps mesuré. En effet pour lui l'objet aura une plus grande inertie. En effet en fonction de sa vitesse, son aceleration deviendra de plus en plus faible.

Cela dit en éspérant que je ne dit pas d'erreur, l'observateur dans le refereiten R' en mouvement par rapport au bidule perçevra la même courbure d'espace-temps créé par la masse du bidule qu'un observteur imobile dans le referentiel de ce même bidule non?

Merci bien

[invite9438e0bf]

On peut aussi convertir les mètres et les seconde via le facteur c. Cela te poses-t-il un problème similaire?

Suggestion: ne plus parler de "masse-énergie".

En terme de convertion d'unité :

Convertir des secondes en mètres via c² :
[s] . [m]/[s] = [m]
C'est tout à fait cohérent.

Convertir des kilogrammes en joules via c² :
[kg] . [m]/[s] = [J]
C'est cohérent seulement si on admet que l'énergie est strictement équivalent à une quantité de mouvement (définition de l'énergie je crois).

Cela me pose effectivement un problème sachant que le photon a une énergie, mais pas de masse (donc une quantité de mouvement nulle puisque p=mv). Et ça me fait réfléchir. Et me permet peut-être de m'approcher de la compréhension des théories actuelles...

Je dois bien admettre que l'énergie du photon est bien réelle... vu ses effets. La théorie dit que c'est "l'impulsion" du photon qui lui donne toute son énergie. Mais j'ai du mal à saisir ce terme d'impulsion.

Toutes ces digressions sur l'équivalence masse-énergie, le rôle de la masse, etc. M'amène à croire à une sorte de spécificité du photon.

Le photon est tellement différent des autres particules, que je serait tenté de penser que le photon N'EST PAS une particule (d'ailleur du coup je me demande ce qui fait que les particules sont des particules : la masse ?)...

Je crois commencer à comprendre que ce pourrait être plutôt une sorte de "vibration" d'une structure "collée" à l'espace-temps, l'amplitude donnant alors l'énergie du "photon" : une vibration n'a évidemment pas de masse et donc le photon suit la courbure de l'espace-temps, comme une vibration suit la corde qu'on secoue (en imaginant tenir une corde par un bout et de lui imprimer un mouvement aller-retour vertical d'un seul coup).

Pour une corde simple je peux me représenter la "phase" et la "fréquence", du fait que la corde vibre dans un plan (phase) et plus ou moins vite (fréquence). Alors pour la structure imaginaire "collée" aux boucles, il faut que je m'imagine donc que la structure peut changer localement (la position du photon) d'amplitude (fréquence), mais pour la phase, j'ai plus de mal... Si vous avez une idée pour représenter ça ?

[invite88ef51f0]

Tout d'abord, il faut voir que ce n'est pas parce qu'on peut exprimer les grandeurs dans les mêmes unités qu'elles sont identiques. En posant c=1, on peut exprimer de la même façon énergie et impulsion, mais ce n'est pas pour autant la même chose.

le photon a une énergie, mais pas de masse (donc une quantité de mouvement nulle puisque p=mv).

Pour un photon, on n'a pas p=mv. On a d'après la relation de de Broglie . Et vu que le photon n'a pas de masse, toute l'énergie provient de la quantité de mouvement (E²-p²=m² avec c=1).

Mais j'ai du mal à saisir ce terme d'impulsion.

L'impulsion, ce n'est rien d'autre que la quantité de mouvement (à quelques subtilités près).

[invite9c9b9968]

Cela me pose effectivement un problème sachant que le photon a une énergie, mais pas de masse (donc une quantité de mouvement nulle puisque p=mv). Et ça me fait réfléchir. Et me permet peut-être de m'approcher de la compréhension des théories actuelles...

Je dois bien admettre que l'énergie du photon est bien réelle... vu ses effets. La théorie dit que c'est "l'impulsion" du photon qui lui donne toute son énergie. Mais j'ai du mal à saisir ce terme d'impulsion.

Tu te places trop souvent dans une intuition classique, ce qui ne fonctionne plus avec des objets ultra-relativistes, et quantique en plus

Toutes ces digressions sur l'équivalence masse-énergie, le rôle de la masse, etc. M'amène à croire à une sorte de spécificité du photon.

Le photon est tellement différent des autres particules, que je serait tenté de penser que le photon N'EST PAS une particule (d'ailleur du coup je me demande ce qui fait que les particules sont des particules : la masse ?)

Pourtant d'autres particules sont aussi de masse nulle : les gluons... En fait, qu'est ce que c'est pour toi une particule ?

Je te suggère de te pencher sur le processus de quantification du champ EM, et sur la représentation des groupes en physique, très riche d'enseignement

[invité576543]

Bonjour,

Convertir des kilogrammes en joules via c² :
[kg] . [m]/[s] = [J]
C'est cohérent seulement si on admet que l'énergie est strictement équivalent à une quantité de mouvement (définition de l'énergie je crois).

Non. C'est cohérent. Point. Même en classique, E = mv²/2 indique que masse et énergie sont reliées dimensionnellement par une vitesse au carré, de même que longueur et durée sont reliées dimensionnellement par une vitesse. Aucune différence de principe.

Cela me pose effectivement un problème sachant que le photon a une énergie, mais pas de masse (donc une quantité de mouvement nulle puisque p=mv).

Non. La quantité de mouvement d'un photon n'est pas nulle. La quantité de mouvement se mesure lors de choc, et un photon absorbé ou émis se traduit par un changement de la quantité de mouvement de ce qui émet ou absorbe. Dire que la quantité de mouvement du photon est nulle est contraire à l'expérience.

Je dois bien admettre que l'énergie du photon est bien réelle... vu ses effets. La théorie dit que c'est "l'impulsion" du photon qui lui donne toute son énergie.

Ca n'a pas de sens. L'énergie n'est pas "donnée" par quoi que ce soit.

Mais j'ai du mal à saisir ce terme d'impulsion.

Normal quand on part de l'idée (erronée) que la quantité de mouvement du photon est nulle.

Toutes ces digressions sur l'équivalence masse-énergie, le rôle de la masse, etc. M'amène à croire à une sorte de spécificité du photon.

Le photon est tellement différent des autres particules, que je serait tenté de penser que le photon N'EST PAS une particule (d'ailleur du coup je me demande ce qui fait que les particules sont des particules : la masse ?)...

Les particules de masse nulle sont particulières, de par leur masse nulle .

Ce qui fait qu'une particule est une particule n'est pas la masse, mais le couple (E, p), le couple de l'énergie et la quantité de mouvement. L'approche classique donne plutôt la primauté à m et v, mais cela ne marche que pour les vitesses faibles.

La vision donnée par la relativité restreinte est celle de (E, p) comme faisant qu'une particule est une particule. La masse, invariante par changement de repère, s'en déduit (m² = E²/c⁴ -p²/c²), ainsi que, plus subtilement, la vitesse. Pour obtenir la vitesse, on procède comme suit: si la masse n'est pas nulle, il existe nécessairement un changement de repère (lorentzien) tel que (E, p) devient (E', 0). La vitesse est la vitesse relative des deux repères. Et si la masse est nulle, la vitesse est c, ce qu'on vérifie en passant à la limite en appliquant le principe précédent.

Cordialement,

[invite9438e0bf]

le photon a une énergie, mais pas de masse (donc une quantité de mouvement nulle puisque p=mv).

En fait la quantité de mouvement d'une "particule" telle que le photon est égale à son énergie :
E²=m²c⁴+p²c²

pour m=0 :
E²=p²c², soit E=pc.

à un facteur c près, la quantité de mouvement est donc bien égal à l'énergie de la particule.

Mais alors ce que je ne comprends pas c'est pourquoi on définit p différemment pour le photo du p d'une particule ?

p=mv n'est valable finalement que pour les particules ayant une masse. Cette définition n'est pas réellement "universelle" alors... je consulte donc M. Internet, et là je découvre que p=γmv en milieu relativiste où


Je comprends alors, qu'à la limite (v->c), γ tend vers l'infini. Alors la masse nulle serait "compensée" par ce gamma relativiste... et E -> c².

Mais alors si E varie (selon la fréquence du photon), on pourrait penser que c varie ?

Je vois bien qu'il y a un truc de faux, alors je cherche la relation entre l'énergie et la fréquence :

photon : la mécanique quantique associe à une radiation électromagnétique monochromatique un corpuscule de masse nulle nommé photon dont l'énergie est : E = hν où h est la constante de Planck.

L'impulsion p du photon est égale à p = E / c = hν / c.

Je constate donc qu'il y deux définitions de p... selon qu'il s'agit d'un photon ou d'une autre particule !

Je reprends donc mon E=pc, avec p=hν/c ; et j'ai donc cette fois E=hν, qui cette fois fait bien varier l'énergie avec la longueur d'onde.

Mais alors, quelle lien entre le p=γmv et le p=hν/c ?
Si on met les deux ensemble ça nous donne :
γmv=hν/c

ou encore :
mvc=hνRACINE[1-(v²/c²)]
m=hνRACINE[1-(v²/c²)]vc

Où on a une définition de la masse qui dépend de la vitesse et de la fréquence ???? Ce qui pour un photon redonne bien m=0. Mais alors n'en tire-t-on pas de conclusion sur les autres particules ?

On peut aussi écrire :
ν=γmvc/h ; qui donne la "fréquence" d'une particule en fonction de sa masse et sa vitesse.

[invité576543]

On peut aussi écrire :
ν=γmvc/h ; qui donne la "fréquence" d'une particule en fonction de sa masse et sa vitesse.

Bonsoir,

Il me semble que ce dont on parle usuellement est la fréquence de de Broglie, qui est différente, c'est mc²(γ-1)/h pour une particule de masse non nulle.

Cordialement,