Rapport périmètre diamètre dans un univers discret.

[doryphore]

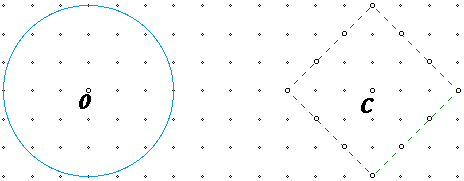
Imaginons un univers plat muni d'une sorte de quadrillage homogène et isotrope et que la longueur d'un objet puisse se trouver en comptant les cases occupée par cet objet...

Dans ce cadre, le rapport entre le périmètre d'un cercle et son diamètre tend vers Pi quand le rayon tend vers l'infini (genre à notre échelle par rapport à celle de Planck) en revanche pour des rayons plus petit, ce rapport n'est plus égal à Pi:

ex: R=1 les rapports possibles sont 8/3 (infiniment probable),3 et 2.
R=2 le rapport le plus probable est 16/5 = 3,2...
R=3 .............................. ...........24/7 ~= 3,43
-----

[Sephi]

Oh oh, ça mérite de creuser un peu ... Ce dont tu parles semble être ce qu'on appelle la taxi-géométrie. Il s'agit d'une géométrie où tous les points de l'espace n'ont que des coordonnées entières (ou qui sont multiples d'une quantité-étalon donnée : la longueur d'un segment du quadrillage). Considérons maintenant un plan quadrillé (aux coordonnées entières : 1 case = 1 unité de longueur), et un point central O.

Un cercle de rayon entier R est défini comme l'ensemble des points à distance R de O. Or, la distance entre deux points en taxi-géométrie est la longueur du plus court chemin reliant ces points, tout en longeant le quadrillage. Avec un peu de réflexion, on voit vite qu'en taxi-géométrie, un cercle devient un carré :

Gauche : cercle usuel de rayon 3 - Droite : taxi-cercle de rayon 3

Comme il s'agit d'un carré, on peut définir le périmètre du cercle comme étant la longueur d'un côté du carré multipliée par 4. La longueur d'un côté vaut le double du rayon, donc le périmètre du cercle vaut 8R.

Le nombre Pi est donné par le rapport périmètre / diamètre, càd 8R/2R = 4. En taxi-géométrie, Pi vaut 4

C'est une forme basique de géométrie non-euclidienne, qui offre de chouettes problèmes récréatifs, avis aux amateurs

[doryphore]

Si un univers est discret, il ne peut donc se limiter à une simple structure métrique de type taxi-géométrie sans quoi les cercles seraient très rares dans la nature.

[doryphore]

Peut-être que si on considère une superposition d'un grand nombre de métrique de ce genre différente par une légère rotation on revient à une distance euclidienne.

[A voir en vidéo sur Futura]