Salut à tous,
Quelqu'un peut-il m'expliquer comment faire une représentation propre à l'ordi des orbitales atomiques d, à la façon de celles sur l'image ci-dessous.
Merci par avance.
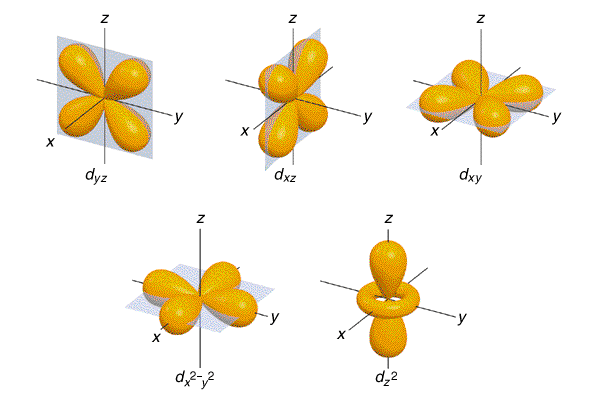
-----


Salut à tous,
Quelqu'un peut-il m'expliquer comment faire une représentation propre à l'ordi des orbitales atomiques d, à la façon de celles sur l'image ci-dessous.
Merci par avance.
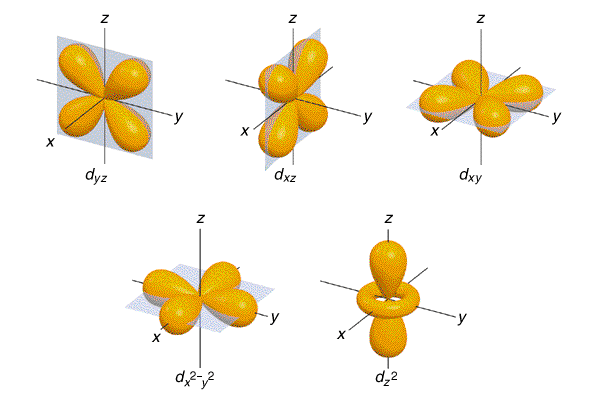

Bonjour,
Cela dépend du logiciel que vous utilisez. Il y a quelques années, j'avais fait ça en Matlab.


Bonjour.
J'avais utilisé une fois Art of Illusion (gratuit) avec lequel on peut faire des animations. Il est très facile à utiliser. Il suffit de faire l'exemple du tutoriel.
On peut jouer sur les éclairages, reflets, etc.
Au revoir.


Bonsoir,
Merci de vos réponses. Personnellement, je code en LaTeX, les graphiques et schémas sont habituellement faits en pstricks ou en tikz mais je suis preneur, à défaut de mieux, d'une source externe pour générer ces graphes. Je vais tester de ce pas Art of illusion.

Si tu connais un peu le numérique, tu peux essayer avec paraview, tu sera beaucoup plus libre (comme sur matlab, à cette différence que paraview est optimisé pour la 3D). En latex laisse tomber, ça sera trop long et compliqué.
Matlab exporte directement en eps, utilisable sur latex, pas paraview. Généralement ce que je fais, c'est que j'exporte une image png en très très haute résolution, que je vectorise en eps par la suite avec vector magic. Ca te donne des eps de très bonne qualité, tu fera ce que tu veux en latex après.
Donc ce que je préconise : matlab pour la 2D, paraview pour la 3D...
Cordialement,
\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/

il y a ce truc là aussi :
http://www.orbitals.com/orb/ov.htm
m@ch3
Never feed the troll after midnight!


Bonjour,
si tu codes en LaTeX, je suis sûr que tu seras séduit par povray. Il te suffit de définir dans un programme une caméra (sa position, le point qu'elle regarde) une ou des sources de lumière, et ensuite tu peux représenter les harmoniques sphériques en utilisant la fonction isosurface.
Je l'ai déjà fait dans une époque lointaine, mais malheureusement je ne retrouve plus le code. Juste pour la frime, voici ce que l'on peut faire avec un peu de pratique :
Ici, ce ne sont pas exactement des orbitales dz2, mais quelquechose qui a la même forme. Là j'ai dû faire un calcul numérique car je faisait la somme de ce paramètre (déplacement chimique observé en RMN) pour tous les atomes du cristal, c'est ce qui donne ce rendu pas très lisse près des sphères vertes. Avec une fonction analytique il n'y aurait pas ce problème.
Cordialement,
Hibou

Sinon, le plus simple est mathematica non?



Merci à tous de vos réponses, c'est sympa
Mon intérêt se porte sur Orbital Viewer et sur Mathematica. N'étant pas un grand spécialiste des harmoniques sphériques, je vais tenter de me faire la main en essayant de représenter sous mathematica les 3 orbitales atomiques 2p sur un même graphe.


@ coussin : la capture d'écran que tu proposes pour les orbitales d provient-elle de ton cru ? Si oui, est-ce possible d'avoir le code source complet ? Ce n'est pas par paresse de ma part, mais n'ayant jamais utilisé mathematica, j'aimerais bien avoir un exemple de code sous les yeux de sorte à y voir plus clair. Merci

Il n'y a pas de code en mathematica wolfram est trop bon mathématicien alors il a déjà tout calculé, on appelle des fonctions prédéfinies dont tu peux lire les expressions directement.

Oui, SphericalHarmonicY[] est une fonction prédéfinie de Mathematica. Y a « rien » à faire


Merci de vos réponses ! À quoi sert la commande PlotRange->All ?
Le terme -i/sqrt{2} correspond à la partie radiale ?
J'ai tenté un essai avec le code :
SphericalPlot3D[-i/Sqrt[2] (SphericalHarmonicY[2, -2, \[Theta], \[Phi]] - SphericalHarmonicY[2, 2, \[Theta], \[Phi]]), {\[Theta], 0, \[Pi]}, {\[Phi], 0, 2 \[Pi]}, PlotRange \[RightArrow] All]
Je me retrouve avec un cube (système d'axes) vide. Qu'ai-je fait qui ne convient pas ?


Finalement, le code précédent marche bien, je n'avais pas saisi le nombre imaginaire "i" comme il le fallait.

